Trees

Tree is slightly more complex than linked list, because the latter(후자) is a linear data structure while the former is not. Tree problems can be solved either breadth-first or depth-first. We have one problem here which is great for practicing breadth-first traversal.

We recommend:

Maximum Depth of Binary Tree,

Validate Binary Search Tree,

Binary Tree Level Order Traversal and

Convert Sorted Array to Binary Search Tree.

	dfs	bfs
[*] Maximum Depth of Binary Tree,	12/2, 12/4, 12/14
[*] Validate Binary Search Tree,	12/4, 12/14, 12/16(완벽)
Symmetric Tree
[*] Binary Tree Level Order Traversal and
[*] Convert Sorted Array to Binary Search Tree.

[*] important

104. Maximum Depth of Binary Tree

leetcode.com/problems/maximum-depth-of-binary-tree/

Given a binary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

3 / \ 9 20 / \ 15 7

return its depth = 3.

Solution

Tree definition

First of all, here is the definition of the TreeNode which we would use.

  /* Definition for a binary tree node. */
  public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
      val = x;
    }
  }

Approach 1: Recursion

Intuition By definition, the maximum depth of a binary tree is the maximum number of steps to reach a leaf node from the root node.

From the definition, an intuitive idea would be to traverse the tree and record the maximum depth during the traversal.

Algorithm

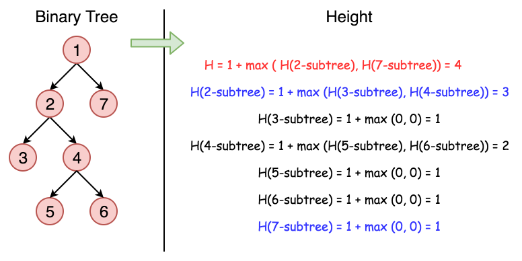
10 / 10

One could traverse the tree either by Depth-First Search (DFS) strategy or Breadth-First Search (BFS) strategy. For this problem, either way would do. Here we demonstrate a solution that is implemented with the DFS strategy and recursion.

class Solution {
    
    public int maxDepth(TreeNode root) {
        
        if(root == null) return 0;
        
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        
        return Math.max(leftHeight, rightHeight)+1;
    }
}

Complexity analysis

Time complexity : we visit each node exactly once, thus the time complexity is \mathcal{O}(N), where N is the number of nodes.
Space complexity : in the worst case, the tree is completely unbalanced, e.g. each node has only left child node, the recursion call would occur N times (the height of the tree), therefore the storage to keep the call stack would be \mathcal{O}(N). But in the best case (the tree is completely balanced), the height of the tree would be \log(N). Therefore, the space complexity in this case would be \mathcal{O}(\log(N)).

Approach 2: Tail Recursion + BFS

One might have noticed that the above recursion solution is probably not the most optimal one in terms of the space complexity, and in the extreme case the overhead of call stack might even lead to stack overflow.

To address the issue, one can tweak the solution a bit to make it tail recursion, which is a specific form of recursion where the recursive call is the last action in the function.

The benefit of having tail recursion, is that for certain programming languages (e.g. C++) the compiler could optimize the memory allocation of call stack by reusing the same space for every recursive call, rather than creating the space for each one. As a result, one could obtain the constant space complexity \mathcal{O}(1) for the overhead of the recursive calls.

Here is a sample solution. Note that the optimization of tail recursion is not supported by Python or Java.

Complexity analysis

Time complexity : \mathcal{O}(N), still we visit each node once and only once.
Space complexity : \mathcal{O}(2^{(log_2N-1)})=\mathcal{O}(N/2)=\mathcal{O}(N), i.e. the maximum number of nodes at the same level (the number of leaf nodes in a full binary tree), since we traverse the tree in the BFS manner.

As one can see, this probably is not the best example to apply the tail recursion technique. Because though we did gain the constant space complexity for the recursive calls, we pay the price of \mathcal{O}(N) complexity to maintain the state information for recursive calls. This defeats the purpose of applying tail recursion.

However, we would like to stress on the point that tail recursion is a useful form of recursion that could eliminate the space overhead incurred by the recursive function calls.

Note: a function cannot be tail recursion if there are multiple occurrences of recursive calls in the function, even if the last action is the recursive call. Because the system has to maintain the function call stack for the sub-function calls that occur within the same function.

Approach 3: Iteration

Intuition

We could also convert the above recursion into iteration, with the help of the stack data structure. Similar with the behaviors of the function call stack, the stack data structure follows the pattern of FILO (First-In-Last-Out), i.e. the last element that is added to a stack would come out first.

With the help of the stack data structure, one could mimic the behaviors of function call stack that is involved in the recursion, to convert a recursive function to a function with iteration.

Algorithm

The idea is to keep the next nodes to visit in a stack. Due to the FILO behavior of stack, one would get the order of visit same as the one in recursion.

We start from a stack which contains the root node and the corresponding depth which is 1. Then we proceed to the iterations: pop the current node out of the stack and push the child nodes. The depth is updated at each step.

class Solution {
  public int maxDepth(TreeNode root) {
    LinkedList<TreeNode> stack = new LinkedList<>();
    LinkedList<Integer> depths = new LinkedList<>();
    if (root == null) return 0;

    stack.add(root);
    depths.add(1);

    int depth = 0, current_depth = 0;
    while(!stack.isEmpty()) {
      root = stack.pollLast();
      current_depth = depths.pollLast();
      if (root != null) {
        depth = Math.max(depth, current_depth);
        stack.add(root.left);
        stack.add(root.right);
        depths.add(current_depth + 1);
        depths.add(current_depth + 1);
      }
    }
    return depth;
  }
};

Complexity analysis

Time complexity : \mathcal{O}(N).
Space complexity : in the worst case, the tree is completely unbalanced, e.g. each node has only left child node, the recursion call would occur N times (the height of the tree), therefore the storage to keep the call stack would be \mathcal{O}(N). But in the average case (the tree is balanced), the height of the tree would be \log(N). Therefore, the space complexity in this case would be \mathcal{O}(\log(N)).

재귀함수 정석코드

class Solution {
    public int maxDepth(TreeNode root) {
        if (root== null){
            return 0;
        }  
         
        return 1 + (Math.max(maxDepth(root.right), maxDepth(root.left)));
    }
}

나는 왜 dfs함수를 새로 만드는 것인가?ㅠㅠ

class Solution {
    
    private ListNode front;
    
    private boolean recursivelyCheck(ListNode current) {
        if(current != null) {
            if(!recursivelyCheck(current.next)) return false;
            if(current.val != front.val) return false;
            front = front.next;
        }
        return true;
    }
    
    public boolean isPalindrome(ListNode head) {
        front = head;
        return recursivelyCheck(head);
    }
}

Time complexity : we visit each node exactly once, thus the time complexity is \mathcal{O}(N), where N is the number of nodes.
Space complexity : in the worst case, the tree is completely unbalanced, e.g. each node has only left child node, the recursion call would occur N times (the height of the tree), therefore the storage to keep the call stack would be \mathcal{O}(N). But in the best case (the tree is completely balanced), the height of the tree would be \log(N). Therefore, the space complexity in this case would be \mathcal{O}(\log(N)).

BFS이렇게 짜면 안되는건가?

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        
        int depth = 0;
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.add(root);
        while(!q.isEmpty()) {
            depth++;
            int sz = q.size();
            while(sz-- > 0) {
                TreeNode node = q.remove();
                if(node.left != null) q.add(node.left);
                if(node.right != null) q.add(node.right);
            }
        }
        return depth;
    }
}

98. Validate Binary Search Tree

leetcode.com/problems/validate-binary-search-tree/

Intuition

On the first sight, the problem is trivial. Let's traverse the tree and check at each step if node.right.val > node.val and node.left.val < node.val. This approach would even work for some trees

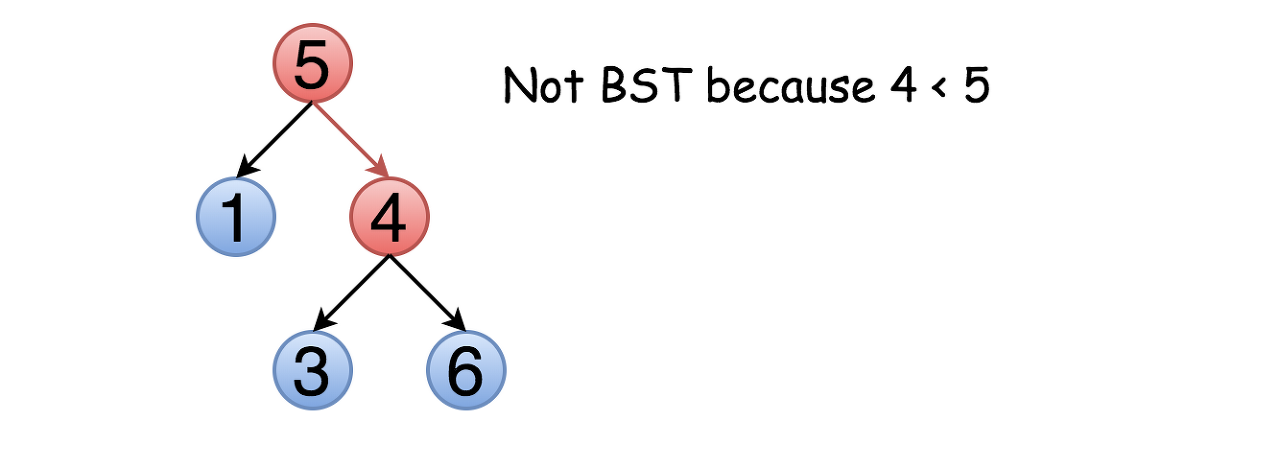
BST를 문제로 받는 순간, 모든 BST에 대해서, 아래의 케이스를 절대 잊으면 안된다.

이 문제의 경우에는 바로 부모랑 비교하는게 아니고 로어랑 어퍼랑 비교해야함.

The problem is this approach will not work for all cases. Not only the right child should be larger than the node but all the elements in the right subtree. Here is an example :

문제는 이 접근법이 모든 경우에 효과가 있지는 않을 것이라는 점이다. 오른쪽 아이는 노드보다 클 뿐만 아니라 오른쪽 하위 트리의 모든 요소들이 커야 한다. 여기 예시가 있다:

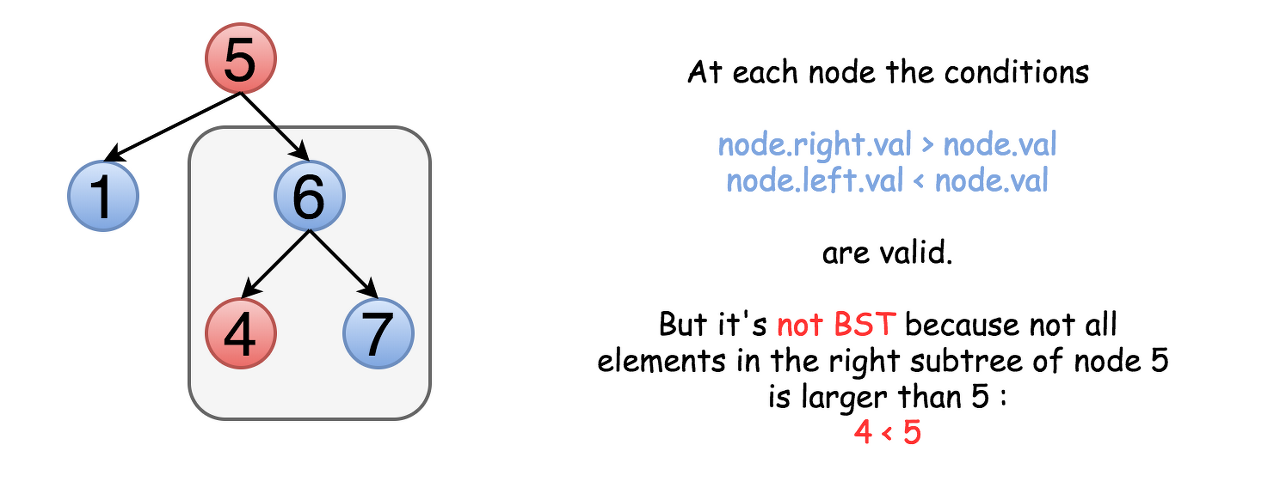
That means one should keep both upper and lower limits for each node while traversing the tree, and compare the node value not with children values but with these limits.

Approach 1: Recursion

The idea above could be implemented as a recursion. One compares the node value with its upper and lower limits if they are available. Then one repeats the same step recursively for left and right subtrees.

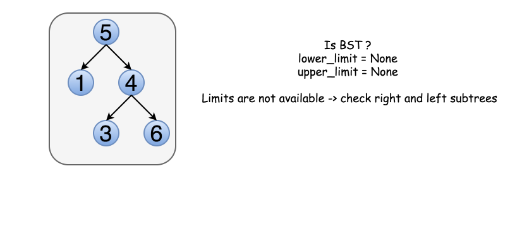
1 / 4

class Solution {
  public boolean helper(TreeNode node, Integer lower, Integer upper) {
    if (node == null) return true;

    int val = node.val;
    if (lower != null && val <= lower) return false;
    if (upper != null && val >= upper) return false;

    if (! helper(node.right, val, upper)) return false;
    if (! helper(node.left, lower, val)) return false;
    return true;
  }

  public boolean isValidBST(TreeNode root) {
    return helper(root, null, null);
  }
}

Complexity Analysis

Time complexity : \mathcal{O}(N) since we visit each node exactly once.
Space complexity : \mathcal{O}(N) since we keep up to the entire tree.

Approach 2: Iteration

The above recursion could be converted into iteration, with the help of stack. DFS would be better than BFS since it works faster here.

class Solution {
  LinkedList<TreeNode> stack = new LinkedList();
  LinkedList<Integer> uppers = new LinkedList(),
          lowers = new LinkedList();

  public void update(TreeNode root, Integer lower, Integer upper) {
    stack.add(root);
    lowers.add(lower);
    uppers.add(upper);
  }

  public boolean isValidBST(TreeNode root) {
    Integer lower = null, upper = null, val;
    update(root, lower, upper);

    while (!stack.isEmpty()) {
      root = stack.poll();
      lower = lowers.poll();
      upper = uppers.poll();

      if (root == null) continue;
      val = root.val;
      if (lower != null && val <= lower) return false;
      if (upper != null && val >= upper) return false;
      update(root.right, val, upper);
      update(root.left, lower, val);
    }
    return true;
  }
}

Complexity Analysis

Time complexity : \mathcal{O}(N) since we visit each node exactly once.
Space complexity : \mathcal{O}(N) since we keep up to the entire tree.

Approach 3: Inorder traversal

Algorithm

Let's use the order of nodes in the inorder traversal Left -> Node -> Right.

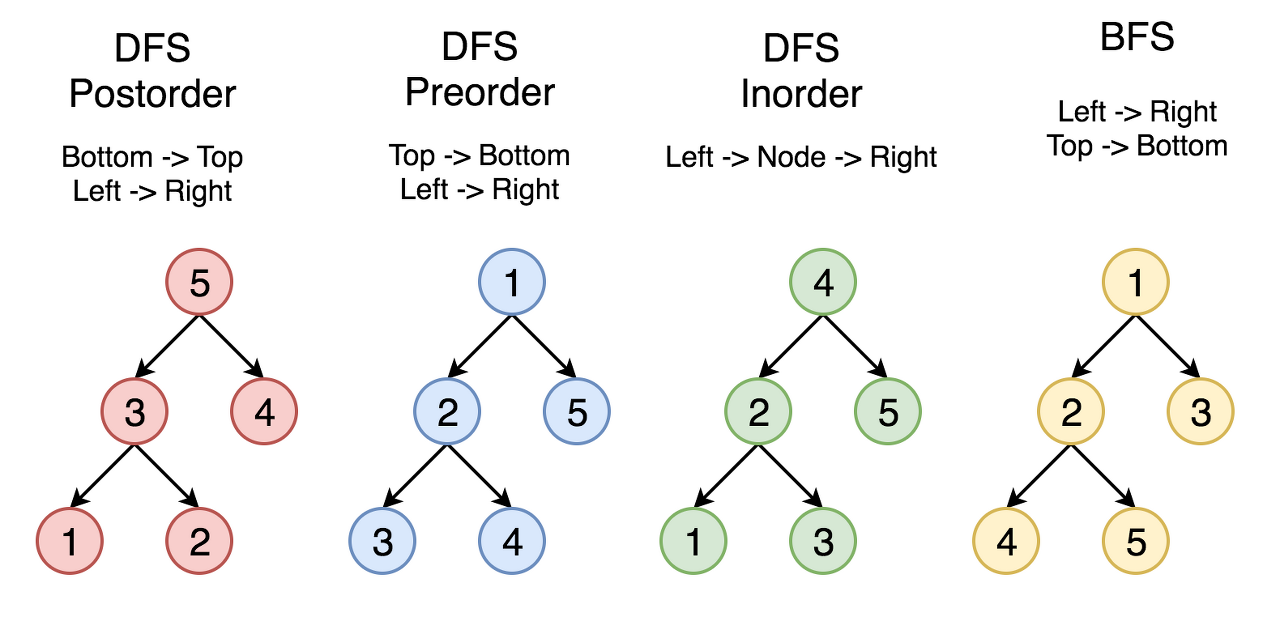
Here the nodes are enumerated in the order you visit them, and you could follow 1-2-3-4-5 to compare different strategies.

Left -> Node -> Right order of inorder traversal means for BST that each element should be smaller than the next one.

Hence the algorithm with \mathcal{O}(N) time complexity and \mathcal{O}(N) space complexity could be simple:

여기 노드는 방문 순서대로 열거되어 있으며, 1-2-3-4-5를 따라 다른 전략을 비교할 수 있다. 왼쪽 -> 노드 -> BST에 대한 순서가 아닌 횡단 수단의 올바른 순서는 각 요소가 다음 요소보다 작아야 합니다. 따라서 MathcalO(N)O(N)O(N) 시간 복잡성과 MathcalO(N)O(N) 공간 복잡성을 갖는 알고리즘은 간단할 수 있다.

Compute inorder traversal list inorder.
Check if each element in inorder is smaller than the next one.

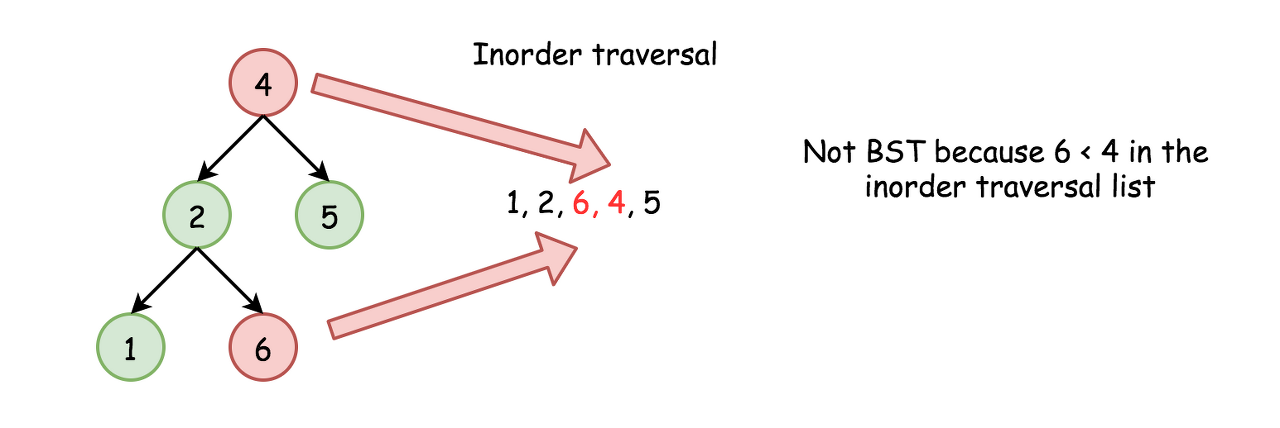
Do we need to keep the whole inorder traversal list?

Actually, no. The last added inorder element is enough to ensure at each step that the tree is BST (or not). Hence one could merge both steps into one and reduce the used space.

class Solution {
  public boolean isValidBST(TreeNode root) {
    Stack<TreeNode> stack = new Stack();
    double inorder = - Double.MAX_VALUE;

    while (!stack.isEmpty() || root != null) {
      while (root != null) {
        stack.push(root);
        root = root.left;
      }
      root = stack.pop();
      // If next element in inorder traversal
      // is smaller than the previous one
      // that's not BST.
      if (root.val <= inorder) return false;
      inorder = root.val;
      root = root.right;
    }
    return true;
  }
}

-Double.MAX_VALUE 와 Double.MIN_VALUE 에는 차이가 있음.

Implementation

Complexity Analysis

Time complexity : \mathcal{O}(N) in the worst case when the tree is BST or the "bad" element is a rightmost leaf.
Space complexity : \mathcal{O}(N) to keep stack.

12/14 try. 신나게 짰지만, 문제의 value기준을 간과하여 테스트케이스 [2147483647]를 받고 wrong answer.

-2^31 <= Node.val <= 2^31 - 1

아래는 틀린코드.

class Solution {
    boolean dfs(TreeNode node, int min, int max) {
        if(node == null) return true;
        
        if(min >= node.val || node.val >= max) return false;
        
        return dfs(node.left, min, node.val) && dfs(node.right, node.val, max);
    }
    public boolean isValidBST(TreeNode root) {
        return dfs(root, Integer.MIN_VALUE, Integer.MAX_VALUE);
    }
}

이게 맞는 코드

class Solution {
    boolean dfs(TreeNode node, TreeNode min, TreeNode max) {
        if(node == null) return true;
        
        if(min != null && min.val >= node.val) return false;
        if(max != null && max.val <= node.val) return false;
        
        return dfs(node.left, min, node) && dfs(node.right, node, max);
    }
    public boolean isValidBST(TreeNode root) {
        return dfs(root, null, null);
    }
}

101. Symmetric Tree

leetcode.com/problems/symmetric-tree/

Solution

Approach 1: Recursive

A tree is symmetric if the left subtree is a mirror reflection of the right subtree.

Therefore, the question is: when are two trees a mirror reflection of each other?

Two trees are a mirror reflection of each other if:

Their two roots have the same value.
The right subtree of each tree is a mirror reflection of the left subtree of the other tree.

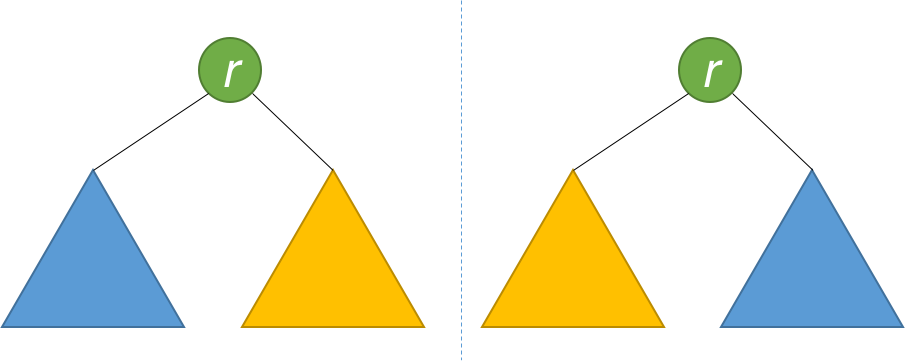
This is like a person looking at a mirror. The reflection in the mirror has the same head, but the reflection's right arm corresponds to the actual person's left arm, and vice versa.

The explanation above translates naturally to a recursive function as follows.

public boolean isSymmetric(TreeNode root) {
    return isMirror(root, root);
}

public boolean isMirror(TreeNode t1, TreeNode t2) {
    if (t1 == null && t2 == null) return true;
    if (t1 == null || t2 == null) return false;
    return (t1.val == t2.val)
        && isMirror(t1.right, t2.left)
        && isMirror(t1.left, t2.right);
}

Complexity Analysis

Time complexity : O(n). Because we traverse the entire input tree once, the total run time is O(n), where n is the total number of nodes in the tree.
Space complexity : The number of recursive calls is bound by the height of the tree. In the worst case, the tree is linear and the height is in O(n). Therefore, space complexity due to recursive calls on the stack is O(n) in the worst case.

Approach 2: Iterative

Instead of recursion, we can also use iteration with the aid of a queue. Each two consecutive nodes in the queue should be equal, and their subtrees a mirror of each other. Initially, the queue contains root and root. Then the algorithm works similarly to BFS, with some key differences. Each time, two nodes are extracted and their values compared. Then, the right and left children of the two nodes are inserted in the queue in opposite order. The algorithm is done when either the queue is empty, or we detect that the tree is not symmetric (i.e. we pull out two consecutive nodes from the queue that are unequal).

public boolean isSymmetric(TreeNode root) {
    Queue<TreeNode> q = new LinkedList<>();
    q.add(root);
    q.add(root);
    while (!q.isEmpty()) {
        TreeNode t1 = q.poll();
        TreeNode t2 = q.poll();
        if (t1 == null && t2 == null) continue;
        if (t1 == null || t2 == null) return false;
        if (t1.val != t2.val) return false;
        q.add(t1.left);
        q.add(t2.right);
        q.add(t1.right);
        q.add(t2.left);
    }
    return true;
}

Complexity Analysis

Time complexity : O(n). Because we traverse the entire input tree once, the total run time is O(n), where n is the total number of nodes in the tree.
Space complexity : There is additional space required for the search queue. In the worst case, we have to insert O(n) nodes in the queue. Therefore, space complexity is O(n).

102. Binary Tree Level Order Traversal

leetcode.com/problems/binary-tree-level-order-traversal/

Solution

How to traverse the tree

There are two general strategies to traverse a tree:

Depth First Search (DFS)

In this strategy, we adopt the depth as the priority, so that one would start from a root and reach all the way down to certain leaf, and then back to root to reach another branch.

The DFS strategy can further be distinguished as preorder, inorder, and postorder depending on the relative order among the root node, left node and right node.
Breadth First Search (BFS)

We scan through the tree level by level, following the order of height, from top to bottom. The nodes on higher level would be visited before the ones with lower levels.

On the following figure the nodes are numerated in the order you visit them, please follow 1-2-3-4-5 to compare different strategies.

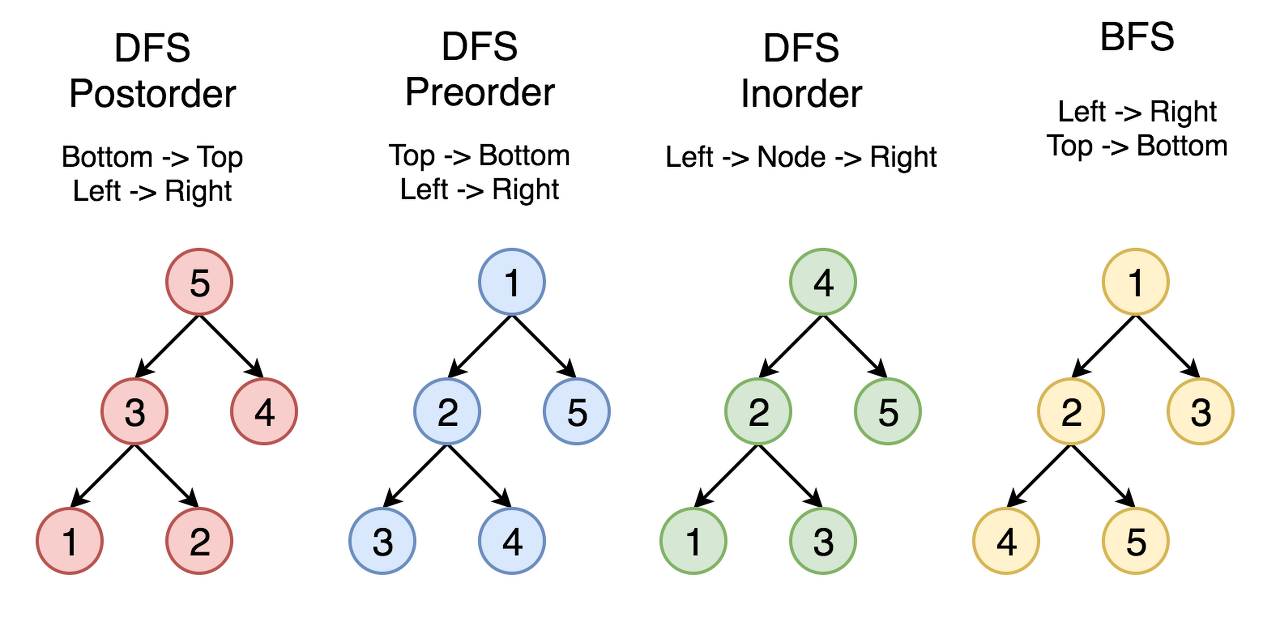
Here the problem is to implement split-level BFS traversal : [[1], [2, 3], [4, 5]].

Approach 1: Recursion

Algorithm

The simplest way to solve the problem is to use a recursion. Let's first ensure that the tree is not empty, and then call recursively the function helper(node, level), which takes the current node and its level as the arguments.

This function does the following :

The output list here is called levels, and hence the current level is just a length of this list len(levels). Compare the number of a current level len(levels) with a node level level. If you're still on the previous level - add the new one by adding a new list into levels.
Append the node value to the last list in levels.
Process recursively child nodes if they are not None : helper(node.left / node.right, level + 1).

Implementation

1 / 15

class Solution {
    List<List<Integer>> levels = new ArrayList<List<Integer>>();

    public void helper(TreeNode node, int level) {
        // start the current level
        if (levels.size() == level)
            levels.add(new ArrayList<Integer>());

         // fulfil the current level
         levels.get(level).add(node.val);

         // process child nodes for the next level
         if (node.left != null)
            helper(node.left, level + 1);
         if (node.right != null)
            helper(node.right, level + 1);
    }
    
    public List<List<Integer>> levelOrder(TreeNode root) {
        if (root == null) return levels;
        helper(root, 0);
        return levels;
    }
}

Complexity Analysis

Time complexity : \mathcal{O}(N) since each node is processed exactly once.
Space complexity : \mathcal{O}(N) to keep the output structure which contains N node values.

Approach 2: Iteration

Algorithm

The recursion above could be rewritten in the iteration form.

Let's keep nodes of each tree level in the queue structure, which typically orders elements in a FIFO (first-in-first-out) manner. In Java one could use LinkedList implementation of the Queue interface. In Python using Queue structure would be an overkill since it's designed for a safe exchange between multiple threads and hence requires locking which leads to a performance loose. In Python the queue implementation with a fast atomic append() and popleft() is deque.

The zero level contains only one node root. The algorithm is simple :

Initiate queue with a root and start from the level number 0 : level = 0.
While queue is not empty :
- Start the current level by adding an empty list into output structure levels.
- Compute how many elements should be on the current level : it's a queue length.
- Pop out all these elements from the queue and add them into the current level.
- Push their child nodes into the queue for the next level.
- Go to the next level level++.

Implementation

class Solution {
  public List<List<Integer>> levelOrder(TreeNode root) {
    List<List<Integer>> levels = new ArrayList<List<Integer>>();
    if (root == null) return levels;

    Queue<TreeNode> queue = new LinkedList<TreeNode>();
    queue.add(root);
    int level = 0;
    while ( !queue.isEmpty() ) {
      // start the current level
      levels.add(new ArrayList<Integer>());

      // number of elements in the current level
      int level_length = queue.size();
      for(int i = 0; i < level_length; ++i) {
        TreeNode node = queue.remove();

        // fulfill the current level
        levels.get(level).add(node.val);

        // add child nodes of the current level
        // in the queue for the next level
        if (node.left != null) queue.add(node.left);
        if (node.right != null) queue.add(node.right);
      }
      // go to next level
      level++;
    }
    return levels;
  }
}

Complexity Analysis

Time complexity : \mathcal{O}(N) since each node is processed exactly once.
Space complexity : \mathcal{O}(N) to keep the output structure which contains N node values.

108. Convert Sorted Array to Binary Search Tree

leetcode.com/problems/convert-sorted-array-to-binary-search-tree/

Solution

How to Traverse the Tree. DFS: Preorder, Inorder, Postorder; BFS.

There are two general strategies to traverse a tree:

Depth First Search (DFS)

In this strategy, we adopt the depth as the priority, so that one would start from a root and reach all the way down to certain leaf, and then back to root to reach another branch.

The DFS strategy can further be distinguished as preorder, inorder, and postorder depending on the relative order among the root node, left node and right node.
Breadth First Search (BFS)

We scan through the tree level by level, following the order of height, from top to bottom. The nodes on higher level would be visited before the ones with lower levels.

On the following figure the nodes are enumerated in the order you visit them, please follow 1-2-3-4-5 to compare different strategies.

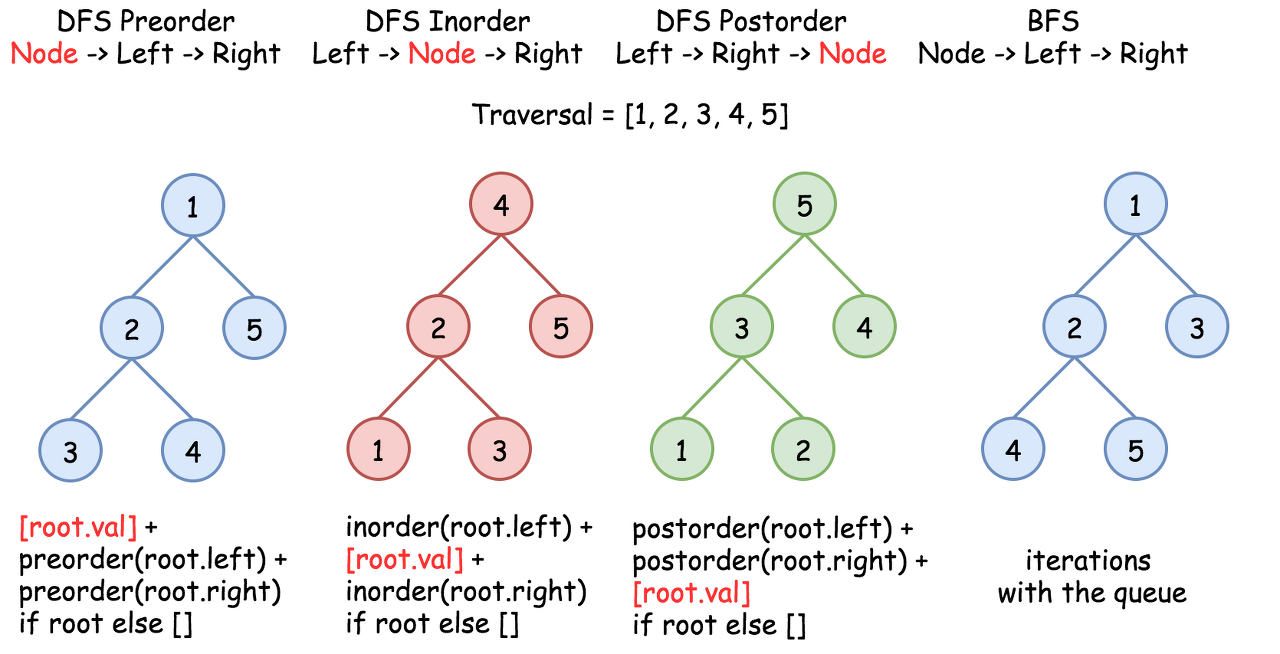
Construct BST from Inorder Traversal: Why the Solution is Not Unique

It's known that inorder traversal of BST is an array sorted in the ascending order.

Having sorted array as an input, we could rewrite the problem as Construct Binary Search Tree from Inorder Traversal.

Does this problem have a unique solution, i.e. could inorder traversal be used as a unique identifier to encore/decode BST? The answer is no.

Here is the funny thing about BST. Inorder traversal is not a unique identifier of BST. At the same time both preorder and postorder traversals are unique identifiers of BST. From these traversals one could restore the inorder one: inorder = sorted(postorder) = sorted(preorder), and inorder + postorder or inorder + preorder are both unique identifiers of whatever binary tree.

So, the problem "sorted array -> BST" has multiple solutions.

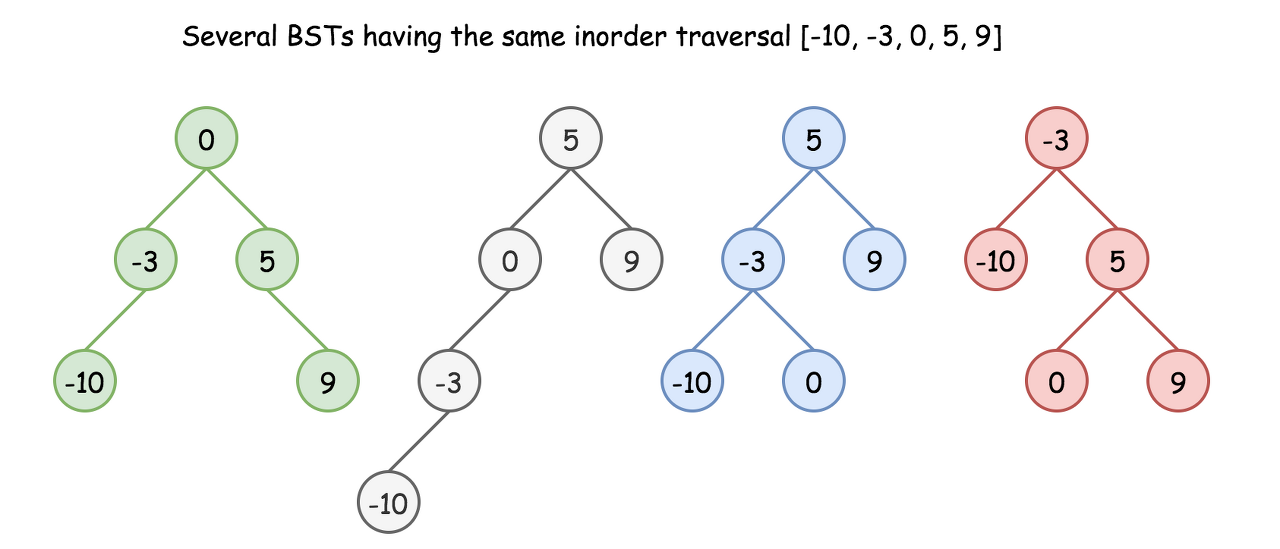
Here we have an additional condition: the tree should be height-balanced, i.e. the depths of the two subtrees of every node never differ by more than 1.

Does it make the solution to be unique? Still no.

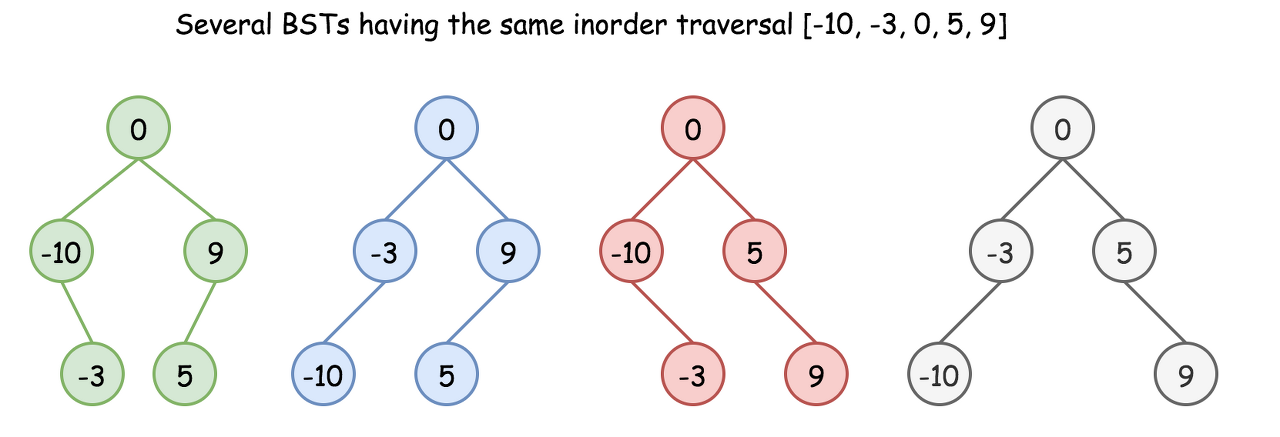
Basically, the height-balanced restriction means that at each step one has to pick up the number in the middle as a root. That works fine with arrays containing odd number of elements but there is no predefined choice for arrays with even number of elements.

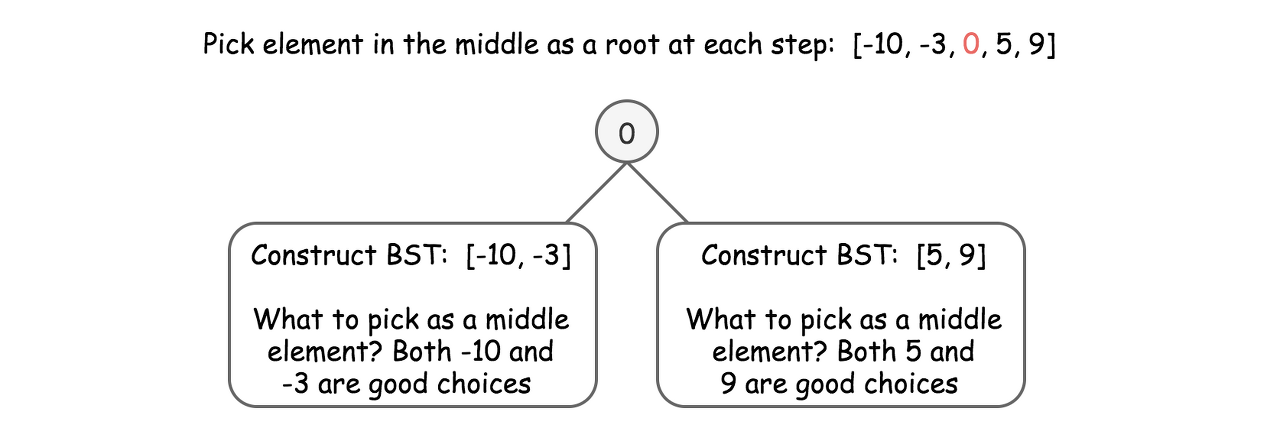
One could choose left middle element, or right middle one, and both choices will lead to different height-balanced BSTs. Let's see that in practice: in Approach 1 we will always pick up left middle element, in Approach 2 - right middle one. That will generate different BSTs but both solutions will be accepted.

Approach 1: Preorder Traversal: Always Choose Left Middle Node as a Root

Algorithm

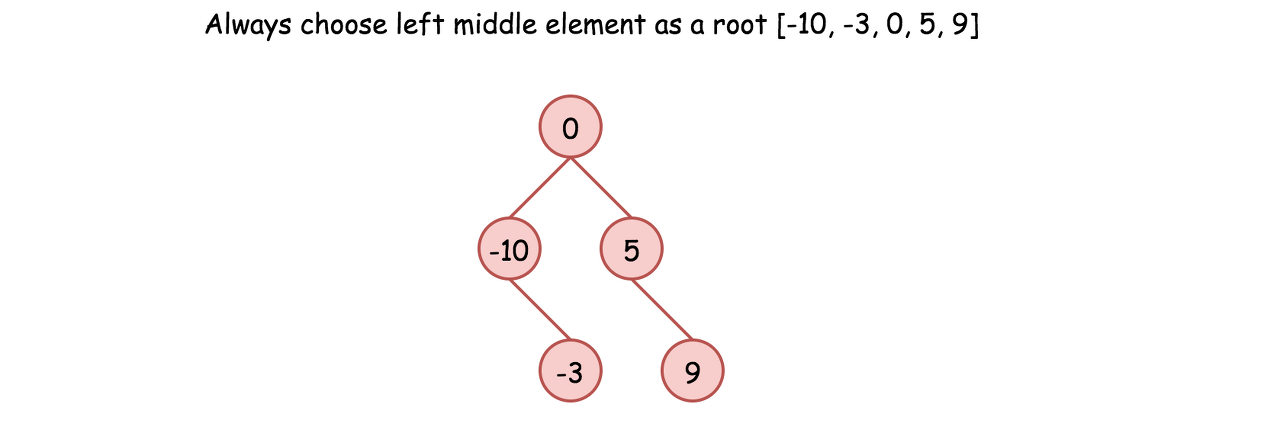
Implement helper function helper(left, right), which constructs BST from nums elements between indexes left and right:
- If left > right, then there is no elements available for that subtree. Return None.
- Pick left middle element: p = (left + right) // 2.
- Initiate the root: root = TreeNode(nums[p]).
- Compute recursively left and right subtrees: root.left = helper(left, p - 1), root.right = helper(p + 1, right).
Return helper(0, len(nums) - 1).

Implementation

class Solution {
  int[] nums;

  public TreeNode helper(int left, int right) {
    if (left > right) return null;

    // always choose left middle node as a root
    int p = (left + right) / 2;

    // preorder traversal: node -> left -> right
    TreeNode root = new TreeNode(nums[p]);
    root.left = helper(left, p - 1);
    root.right = helper(p + 1, right);
    return root;
  }

  public TreeNode sortedArrayToBST(int[] nums) {
    this.nums = nums;
    return helper(0, nums.length - 1);
  }
}

Complexity Analysis

Time complexity: \mathcal{O}(N) since we visit each node exactly once.
Space complexity: \mathcal{O}(N). \mathcal{O}(N) to keep the output, and \mathcal{O}(\log N) for the recursion stack.

Approach 2: Preorder Traversal: Always Choose Right Middle Node as a Root

Algorithm

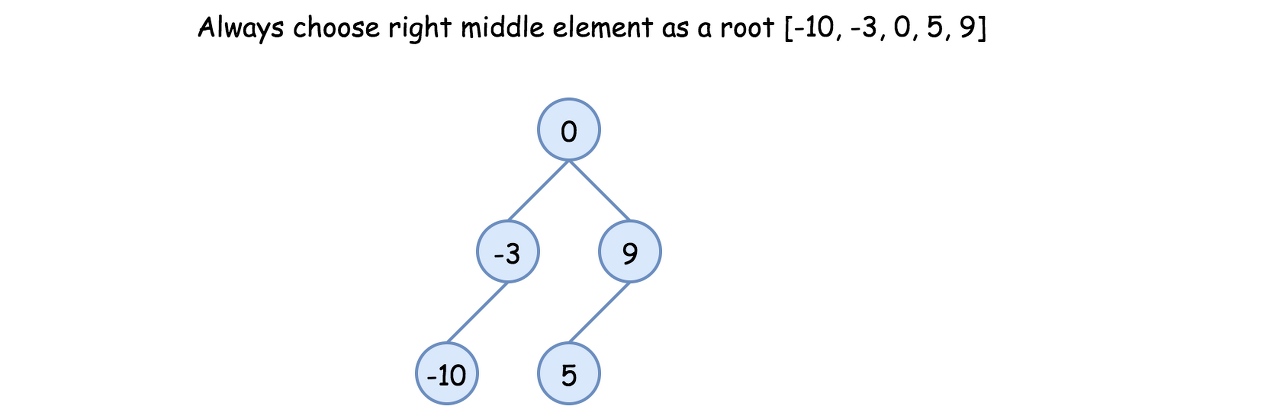
Implement helper function helper(left, right), which constructs BST from nums elements between indexes left and right:
- If left > right, then there is no elements available for that subtree. Return None.
- Pick right middle element:
  - p = (left + right) // 2.
  - If left + right is odd, add 1 to p-index.
- Initiate the root: root = TreeNode(nums[p]).
- Compute recursively left and right subtrees: root.left = helper(left, p - 1), root.right = helper(p + 1, right).
Return helper(0, len(nums) - 1).

Implementation

class Solution {
  int[] nums;

  public TreeNode helper(int left, int right) {
    if (left > right) return null;

    // always choose right middle node as a root
    int p = (left + right) / 2;
    if ((left + right) % 2 == 1) ++p;

    // preorder traversal: node -> left -> right
    TreeNode root = new TreeNode(nums[p]);
    root.left = helper(left, p - 1);
    root.right = helper(p + 1, right);
    return root;
  }

  public TreeNode sortedArrayToBST(int[] nums) {
    this.nums = nums;
    return helper(0, nums.length - 1);
  }
}

Complexity Analysis

Time complexity: \mathcal{O}(N) since we visit each node exactly once.
Space complexity: \mathcal{O}(N). \mathcal{O}(N) to keep the output, and \mathcal{O}(\log N) for the recursion stack.

Approach 3: Preorder Traversal: Choose Random Middle Node as a Root

This one is for fun. Instead of predefined choice we will pick randomly left or right middle node at each step. Each run will result in different solution and they all will be accepted.

Algorithm

Implement helper function helper(left, right), which constructs BST from nums elements between indexes left and right:
- If left > right, then there is no elements available for that subtree. Return None.
- Pick random middle element:
  - p = (left + right) // 2.
  - If left + right is odd, add randomly 0 or 1 to p-index.
- Initiate the root: root = TreeNode(nums[p]).
- Compute recursively left and right subtrees: root.left = helper(left, p - 1), root.right = helper(p + 1, right).
Return helper(0, len(nums) - 1).

Implementation

class Solution {
    int[] nums;
    Random rand = new Random();
    
    public TreeNode helper(int left, int right) {
        if (left > right) return null;
        
        // choose random middle node as a root
        int p = (left + right) / 2; 
        if ((left + right) % 2 == 1) p += rand.nextInt(2);

        // preorder traversal: node -> left -> right
        TreeNode root = new TreeNode(nums[p]);
        root.left = helper(left, p - 1);
        root.right = helper(p + 1, right);
        return root;
    }
    
    public TreeNode sortedArrayToBST(int[] nums) {
        this.nums = nums;
        return helper(0, nums.length - 1);    
    }
}

Complexity Analysis

Time complexity: \mathcal{O}(N) since we visit each node exactly once.
Space complexity: \mathcal{O}(N). \mathcal{O}(N) to keep the output, and \mathcal{O}(\log N) for the recursion stack.