Others

Here are some other questions that do not fit in other categories.

We recommend:

Number of 1 Bits

Valid Parentheses.

191. Number of 1 Bits

Write a function that takes an unsigned integer and returns the number of '1' bits it has (also known as the Hamming weight).

Note:

Note that in some languages such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
In Java, the compiler represents the signed integers using 2's complement notation. Therefore, in Example 3 above, the input represents the signed integer. -3.

Follow up: If this function is called many times, how would you optimize it?

Example 1:

Input: n = 00000000000000000000000000001011 Output: 3 Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits.

Example 2:

Input: n = 00000000000000000000000010000000 Output: 1 Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit.

Example 3:

Input: n = 11111111111111111111111111111101 Output: 31 Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits.

Constraints:

The input must be a binary string of length 32

python code:

return bin(n).count('1')

2.Using bit operation to cancel a 1 in each round

Think of a number in binary n = XXXXXX1000, n - 1 is XXXXXX0111. n & (n - 1) will be XXXXXX0000 which is just remove the last significant 1

def hammingWeight(self, n):
    """
    :type n: int
    :rtype: int
    """
    c = 0
    while n:
        n &= n - 1
        c += 1
    return c

Solution

Approach #1 (Loop and Flip) [Accepted]

** Algorithm**

The solution is straight-forward. We check each of the 32 bits of the number. If the bit is 1, we add one to the number of 1-bits.

We can check the i^{th} bit of a number using a bit mask. We start with a mask m=1, because the binary representation of 1 is,

0000 0000 0000 0000 0000 0000 0000 0001 Clearly, a logical AND between any number and the mask 1 gives us the least significant bit of this number. To check the next bit, we shift the mask to the left by one.

0000 0000 0000 0000 0000 0000 0000 0010

And so on.

Java

public int hammingWeight(int n) {
    int bits = 0;
    int mask = 1;
    for (int i = 0; i < 32; i++) {
        if ((n & mask) != 0) {
            bits++;
        }
        mask <<= 1;
    }
    return bits;
}

Complexity Analysis

The run time depends on the number of bits in n. Because n in this piece of code is a 32-bit integer, the time complexity is O(1).

The space complexity is O(1), since no additional space is allocated.

Approach #2 (Bit Manipulation Trick) [Accepted]

Algorithm

We can make the previous algorithm simpler and a little faster. Instead of checking every bit of the number, we repeatedly flip the least-significant 1-bit of the number to 0, and add 1 to the sum. As soon as the number becomes 0, we know that it does not have any more 1-bits, and we return the sum.

The key idea here is to realize that for any number n, doing a bit-wise AND of n and n - 1 flips the least-significant 1-bit in n to 0. Why? Consider the binary representations of n and n - 1.

Figure 1. AND-ing n and n-1 flips the least-significant 1-bit to 0.

In the binary representation, the least significant 1-bit in n always corresponds to a 0-bit in n - 1. Therefore, anding the two numbers n and n - 1 always flips the least significant 1-bit in n to 0, and keeps all other bits the same.

Using this trick, the code becomes very simple.

Java

public int hammingWeight(int n) {
    int sum = 0;
    while (n != 0) {
        sum++;
        n &= (n - 1);
    }
    return sum;
}

Complexity Analysis

The run time depends on the number of 1-bits in n. In the worst case, all bits in n are 1-bits. In case of a 32-bit integer, the run time is O(1).

The space complexity is O(1), since no additional space is allocated.

Analysis written by: @noran.

이런 코드도..

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        if (n == 0)
            return 0;
        int count = 0;
        int x = n;
        while (x != 0)
        {
            int lastBit = (x  & 1);
            //System.out.print(lastBit);
            if (lastBit == 1)
                count++;
            x = (x >>> 1);
        }
        return count;
    }
}

461. Hamming Distance

leetcode.com/problems/hamming-distance/

The Hamming distance between two integers is the number of positions at which the corresponding bits are different.

Given two integers x and y, calculate the Hamming distance.

Note:
0 ≤ x, y < 231.

Example:

Input: x = 1, y = 4 Output: 2 Explanation: 1 (0 0 0 1) 4 (0 1 0 0) ↑ ↑ The above arrows point to positions where the corresponding bits are different.

Solution

Intuition

Hamming distance is an interesting metric that is widely applied in several domains, e.g. in coding theory for error detection, in information theory for quantifying the difference between strings.

The Hamming distance between two integer numbers is the number of positions at which the corresponding bits are different.

Given the above definition, it might remind one of the bit operation called XOR which outputs 1 if and only if the input bits are different.

As a result, in order to measure the hamming distance between x and y, we can first do x XOR y operation, then we simply count the number of bit 1 in the result of XOR operation.

We now convert the original problem into a bit-counting problem. There are several ways to count the bits though, as we will discuss in the following sections.

Approach 1: Built-in BitCounting Functions

Intuition

First of all, let us talk of the elephant in the room. As one can imagine, we have various built-in functions that could count the bit 1 for us, in all (or at least most of) programming languages. So if this is the task that one is asked in a project, then one should probably just go for it, rather than reinventing the wheel. We given two examples in the following.

Now, since this is a LeetCode problem, some of you would argue that using the built-in function is like "implementing a LinkedList with LinkedList", which we fully second as well. So no worry, we will see later some fun hand-crafted algorithms for bit counting.

Algorithm

class Solution {
    public int hammingDistance(int x, int y) {
        return Integer.bitCount(x ^ y); 
    }
}

Complexity Analysis

Time Complexity: \mathcal{O}(1)
- There are two operations in the algorithm. First, we do the XOR operation which takes a constant time.
- Then, we call the built-in bitCount function. In the worst scenario, the function would take \mathcal{O}(k) time where k is the number of bits for an integer number. Since the Integer type is of fixed size in both Python and Java, the overall time complexity of the algorithm becomes constant, regardless the input numbers.
Space Complexity: \mathcal{O}(1), a temporary memory of constant size is consumed, to hold the result of XOR operation.
- We assume that the built-in function also takes a constant space.

Approach 2: Bit Shift

Intuition

In order to count the number of bit 1, we could shift each of the bit to either the leftmost or the rightmost position and then check if the bit is one or not.

More precisely, we should do the logical shift where zeros are shifted in to replace the discarded bits.

Here we adopt the right shift operation, where each bit would has its turn to be shifted to the rightmost position. Once shifted, we then check if the rightmost bit is one, which we can use either the modulo operation (i.e. i % 2) or the bit AND operation (i.e. i & 1). Both operations would mask out the rest of the bits other than the rightmost bit.

Algorithm

class Solution {
  public int hammingDistance(int x, int y) {
    int xor = x ^ y;
    int distance = 0;
    while (xor != 0) {
      if (xor % 2 == 1)
        distance += 1;
      xor = xor >> 1;
    }
    return distance;
  }
}

Complexity Analysis

Time Complexity: \mathcal{O}(1), since the Integer is of fixed size in Python and Java, the algorithm takes a constant time. For an Integer of 32 bit, the algorithm would take at most 32 iterations.
Space Complexity: \mathcal{O}(1), a constant size of memory is used, regardless the input.

Approach 3: Brian Kernighan's Algorithm

Intuition

In the above approach, one might wonder that "rather than shifting the bits one by one, is there a faster way to count the bits of one ?". And the answer is yes.

If we is asked to count the bits of one, as humans, rather than mechanically examining each bit, we could skip the bits of zero in between the bits of one, e.g. 10001000.

In the above example, after encountering the first bit of one at the rightmost position, it would be more efficient if we just jump at the next bit of one, skipping all the zeros in between.

This is the basic idea of the Brian Kernighan's bit counting algorithm, which applies some smart bit and arithmetic operations to clear the rightmost bit of one. Here is the secret recipe.

When we do AND bit operation between number and number-1, the rightmost bit of one in the original number would be cleared.

Based on the above idea, we then can count the bits of one for the input of 10001000 in 2 iterations, rather than 8.

Algorithm

Note, according to the online book of Bit Twiddling Hacks, the algorithm was published as an exercise in 1988, in the book of the C Programming Language 2nd Ed. (by Brian W. Kernighan and Dennis M. Ritchie), though on April 19, 2006 Donald Knuth pointed out that this method "was first published by Peter Wegner in CACM 3 (1960), 322. (Also discovered independently by Derrick Lehmer and published in 1964 in a book edited by Beckenbach.)". By the way, one can find many other tricks about bit operations in the aforementioned book.

class Solution {
  public int hammingDistance(int x, int y) {
    int xor = x ^ y;
    int distance = 0;
    while (xor != 0) {
      distance += 1;
      // remove the rightmost bit of '1'
      xor = xor & (xor - 1);
    }
    return distance;
  }
}

Complexity Analysis

Time Complexity: \mathcal{O}(1).
- Similar as the approach of bit shift, since the size (i.e. bit number) of integer number is fixed, we have a constant time complexity.
- However, this algorithm would require less iterations than the bit shift approach, as we have discussed in the intuition.
Space Complexity: \mathcal{O}(1), a constant size of memory is used, regardless the input.

190. Reverse Bits

leetcode.com/problems/reverse-bits/

Easy

1476496Add to ListShare

Reverse bits of a given 32 bits unsigned integer.

Note:

Note that in some languages such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
In Java, the compiler represents the signed integers using 2's complement notation. Therefore, in Example 2 above, the input represents the signed integer -3 and the output represents the signed integer -1073741825.

Follow up:

If this function is called many times, how would you optimize it?

Example 1:

Input: n = 00000010100101000001111010011100 Output: 964176192 (00111001011110000010100101000000) Explanation: The input binary string 00000010100101000001111010011100 represents the unsigned integer 43261596, so return 964176192 which its binary representation is 00111001011110000010100101000000.

Example 2:

Input: n = 11111111111111111111111111111101 Output: 3221225471 (10111111111111111111111111111111) Explanation: The input binary string 11111111111111111111111111111101 represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is 10111111111111111111111111111111.

Constraints:

The input must be a binary string of length 32

118. Pascal's Triangle

leetcode.com/problems/pascals-triangle/

Easy

2080123Add to ListShare

Given a non-negative integer numRows, generate the first numRows of Pascal's triangle.

In Pascal's triangle, each number is the sum of the two numbers directly above it.

Example:

Input: 5 Output: [ [1], [1,1], [1,2,1], [1,3,3,1], [1,4,6,4,1] ]

Approach 1: Dynamic Programming

Intuition

If we have the a row of Pascal's triangle, we can easily compute the next row by each pair of adjacent values.

Algorithm

Although the algorithm is very simple, the iterative approach to constructing Pascal's triangle can be classified as dynamic programming because we construct each row based on the previous row.

First, we generate the overall triangle list, which will store each row as a sublist. Then, we check for the special case of 0, as we would otherwise return [1]. If numRows > 0, then we initialize triangle with [1] as its first row, and proceed to fill the rows as follows:

1 / 12

Complexity Analysis

Time complexity : O(numRows^2)

Although updating each value of triangle happens in constant time, it is performed O(numRows^2) times. To see why, consider how many overall loop iterations there are. The outer loop obviously runs numRows times, but for each iteration of the outer loop, the inner loop runs rowNum times. Therefore, the overall number of triangle updates that occur is 1 + 2 + 3 + \ldots + numRows, which, according to Gauss' formula, is

\begin{aligned} \frac{numRows(numRows+1)}{2} &= \frac{numRows^2 + numRows}{2} \\ &= \frac{numRows^2}{2} + \frac{numRows}{2} \\ &= O(numRows^2) \end{aligned}
Space complexity : O(numRows^2)

Because we need to store each number that we update in triangle, the space requirement is the same as the time complexity.

20. Valid Parentheses

leetcode.com/problems/valid-parentheses/

Easy

6391263Add to ListShare

Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.

An input string is valid if:

Open brackets must be closed by the same type of brackets.
Open brackets must be closed in the correct order.

Example 1:

Input: s = "()" Output: true

Example 2:

Input: s = "()[]{}" Output: true

Example 3:

Input: s = "(]" Output: false

Example 4:

Input: s = "([)]" Output: false

Example 5:

Input: s = "{[]}" Output: true

Constraints:

1 <= s.length <= 104
s consists of parentheses only '()[]{}'.

Solution

Intuition

Imagine you are writing a small compiler for your college project and one of the tasks (or say sub-tasks) for the compiler would be to detect if the parenthesis are in place or not.

The algorithm we will look at in this article can be then used to process all the parenthesis in the program your compiler is compiling and checking if all the parenthesis are in place. This makes checking if a given string of parenthesis is valid or not, an important programming problem.

The expressions that we will deal with in this problem can consist of three different type of parenthesis:

(),
{} and
[]

Before looking at how we can check if a given expression consisting of these parenthesis is valid or not, let us look at a simpler version of the problem that consists of just one type of parenthesis. So, the expressions we can encounter in this simplified version of the problem are e.g.

(((((()))))) -- VALID ()()()() -- VALID (((((((() -- INVALID ((()(()))) -- VALID

Let's look at a simple algorithm to deal with this problem.

We process the expression one bracket at a time starting from the left.
Suppose we encounter an opening bracket i.e. (, it may or may not be an invalid expression because there can be a matching ending bracket somewhere in the remaining part of the expression. Here, we simply increment the counter keeping track of left parenthesis till now. left += 1
If we encounter a closing bracket, this has two meanings:
1. One, there was no matching opening bracket for this closing bracket and in that case we have an invalid expression. This is the case when left == 0 i.e. when there are no unmatched left brackets available.
2. We had some unmatched opening bracket available to match this closing bracket. This is the case when left > 0 i.e. we have unmatched left brackets available.
If we encounter a closing bracket i.e. ) when left == 0, then we have an invalid expression on our hands. Else, we decrement left thus reducing the number of unmatched left parenthesis available.
Continue processing the string until all parenthesis have been processed.
If in the end we still have unmatched left parenthesis available, this implies an invalid expression.

The reason we discussed this particular algorithm here is because the approach for the original problem derives its inspiration from this very solution. Have a look at the following dry run of the algorithm we discussed to have a better understanding.

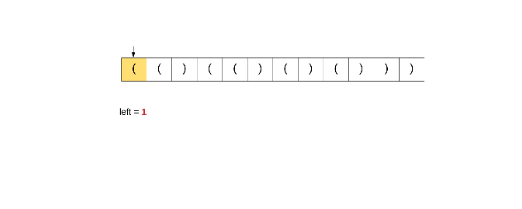
1 / 12

If we try and follow the same approach for our original problem, then it simply won't work. The reason a simple counter based approach works above is because all the parenthesis are of the same type. So when we encounter a closing bracket, we simply assume a corresponding opening matching bracket to be available i.e. if left > 0.

But, in our problem, if we encounter say ], we don't really know if there is a corresponding opening [ available or not. You could say:

Why not maintain a separate counter for the different types of parenthesis?

This doesn't work because the relative placement of the parenthesis also matters here. e.g.:

[{]

If we simply keep counters here, then as soon as we encounter the closing square bracket, we would know there is an unmatched opening square bracket available as well. But, the closest unmatched opening bracket available is a curly bracket and not a square bracket and hence the counting approach breaks here.

Approach 1: Stacks

An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.

Also, if you look at the above structure carefully, the color coded cells mark the opening and closing pairs of parenthesis. The entire expression is valid, but sub portions of it are also valid in themselves. This lends a sort of a recursive structure to the problem. For e.g. Consider the expression enclosed within the two green parenthesis in the diagram above. The opening bracket at index 1 and the corresponding closing bracket at index 6.

What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression?

Let's have a look at this idea below where remove the smaller expressions one at a time from the overall expression and since this is a valid expression, we would be left with an empty string in the end.

1 / 5

The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards.

Let us have a look at the algorithm for this problem using stacks as the intermediate data structure.

Algorithm

Initialize a stack S.
Process each bracket of the expression one at a time.
If we encounter an opening bracket, we simply push it onto the stack. This means we will process it later, let us simply move onto the sub-expression ahead.
If we encounter a closing bracket, then we check the element on top of the stack. If the element at the top of the stack is an opening bracket of the same type, then we pop it off the stack and continue processing. Else, this implies an invalid expression.
In the end, if we are left with a stack still having elements, then this implies an invalid expression.

We'll have a look a dry run for the algorithm and then move onto the implementation.

1 / 12

Let us now have a look at the implementation for this algorithm.

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """

        # The stack to keep track of opening brackets.
        stack = []

        # Hash map for keeping track of mappings. This keeps the code very clean.
        # Also makes adding more types of parenthesis easier
        mapping = {")": "(", "}": "{", "]": "["}

        # For every bracket in the expression.
        for char in s:

            # If the character is an closing bracket
            if char in mapping:

                # Pop the topmost element from the stack, if it is non empty
                # Otherwise assign a dummy value of '#' to the top_element variable
                top_element = stack.pop() if stack else '#'

                # The mapping for the opening bracket in our hash and the top
                # element of the stack don't match, return False
                if mapping[char] != top_element:
                    return False
            else:
                # We have an opening bracket, simply push it onto the stack.
                stack.append(char)

        # In the end, if the stack is empty, then we have a valid expression.
        # The stack won't be empty for cases like ((()
        return not stack

Complexity analysis

Time complexity : O(n) because we simply traverse the given string one character at a time and push and pop operations on a stack take O(1) time.
Space complexity : O(n) as we push all opening brackets onto the stack and in the worst case, we will end up pushing all the brackets onto the stack. e.g. ((((((((((.

268. Missing Number

leetcode.com/problems/missing-number/

Easy

24182408Add to ListShare

Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.

Follow up: Could you implement a solution using only O(1) extra space complexity and O(n) runtime complexity?

Example 1:

Input: nums = [3,0,1] Output: 2 Explanation: n = 3 since there are 3 numbers, so all numbers are in the range [0,3]. 2 is the missing number in the range since it does not appear in nums.

Example 2:

Input: nums = [0,1] Output: 2 Explanation: n = 2 since there are 2 numbers, so all numbers are in the range [0,2]. 2 is the missing number in the range since it does not appear in nums.

Example 3:

Input: nums = [9,6,4,2,3,5,7,0,1] Output: 8 Explanation: n = 9 since there are 9 numbers, so all numbers are in the range [0,9]. 8 is the missing number in the range since it does not appear in nums.

Example 4:

Input: nums = [0] Output: 1 Explanation: n = 1 since there is 1 number, so all numbers are in the range [0,1]. 1 is the missing number in the range since it does not appear in nums.

Constraints:

n == nums.length
1 <= n <= 104
0 <= nums[i] <= n
All the numbers of nums are unique.

Approach #1 Sorting [Accepted]

Intuition

If nums were in order, it would be easy to see which number is missing.

Algorithm

First, we sort nums. Then, we check the two special cases that can be handled in constant time - ensuring that 0 is at the beginning and that n is at the end. Given that those assumptions hold, the missing number must somewhere between (but not including) 0 and n. To find it, we ensure that the number we expect to be at each index is indeed there. Because we handled the edge cases, this is simply the previous number plus 1. Thus, as soon as we find an unexpected number, we can simply return the expected number.

Complexity Analysis

Time complexity : \mathcal{O}(nlgn)

The only elements of the algorithm that have asymptotically nonconstant time complexity are the main for loop (which runs in \mathcal{O}(n) time), and the sort invocation (which runs in \mathcal{O}(nlgn) time for Python and Java). Therefore, the runtime is dominated by sort, and the entire runtime is \mathcal{O}(nlgn).
Space complexity : \mathcal{O}(1) (or \mathcal{O}(n))

In the sample code, we sorted nums in place, allowing us to avoid allocating additional space. If modifying nums is forbidden, we can allocate an \mathcal{O}(n) size copy and sort that instead.

Approach #2 HashSet [Accepted]

Intuition

A brute force method for solving this problem would be to simply check for the presence of each number that we expect to be present. The naive implementation might use a linear scan of the array to check for containment, but we can use a HashSet to get constant time containment queries and overall linear runtime.

Algorithm

This algorithm is almost identical to the brute force approach, except we first insert each element of nums into a set, allowing us to later query for containment in \mathcal{O}(1) time.

Complexity Analysis

Time complexity : \mathcal{O}(n)

Because the set allows for \mathcal{O}(1) containment queries, the main loop runs in \mathcal{O}(n) time. Creating num_set costs \mathcal{O}(n) time, as each set insertion runs in amortized \mathcal{O}(1) time, so the overall runtime is \mathcal{O}(n + n) = \mathcal{O}(n).
Space complexity : \mathcal{O}(n)

nums contains n-1 distinct elements, so it costs \mathcal{O}(n) space to store a set containing all of them.

Approach #3 Bit Manipulation [Accepted]

Intuition

We can harness the fact that XOR is its own inverse to find the missing element in linear time.

Algorithm

Because we know that nums contains n numbers and that it is missing exactly one number on the range [0..n-1], we know that n definitely replaces the missing number in nums. Therefore, if we initialize an integer to n and XOR it with every index and value, we will be left with the missing number. Consider the following example (the values have been sorted for intuitive convenience, but need not be):

IndexValue

0	1	2	3
0	1	3	4

\begin{aligned} missing &= 4 \wedge (0 \wedge 0) \wedge (1 \wedge 1) \wedge (2 \wedge 3) \wedge (3 \wedge 4) \\ &= (4 \wedge 4) \wedge (0 \wedge 0) \wedge (1 \wedge 1) \wedge (3 \wedge 3) \wedge 2 \\ &= 0 \wedge 0 \wedge 0 \wedge 0 \wedge 2 \\ &= 2 \end{aligned}

class Solution:
    def missingNumber(self, nums):
        missing = len(nums)
        for i, num in enumerate(nums):
            missing ^= i ^ num
        return missing

Complexity Analysis

Time complexity : \mathcal{O}(n)

Assuming that XOR is a constant-time operation, this algorithm does constant work on n iterations, so the runtime is overall linear.
Space complexity : \mathcal{O}(1)

This algorithm allocates only constant additional space.

Approach #4 Gauss' Formula [Accepted]

Intuition

One of the most well-known stories in mathematics is of a young Gauss, forced to find the sum of the first 100 natural numbers by a lazy teacher. Rather than add the numbers by hand, he deduced a closed-form expression for the sum, or so the story goes. You can see the formula below:

\sum_{i=0}^{n}i = \frac{n(n+1)}{2}

Algorithm

We can compute the sum of nums in linear time, and by Gauss' formula, we can compute the sum of the first n natural numbers in constant time. Therefore, the number that is missing is simply the result of Gauss' formula minus the sum of nums, as nums consists of the first n natural numbers minus some number.

class Solution:
    def missingNumber(self, nums):
        expected_sum = len(nums)*(len(nums)+1)//2
        actual_sum = sum(nums)
        return expected_sum - actual_sum

Complexity Analysis

Time complexity : \mathcal{O}(n)

Although Gauss' formula can be computed in \mathcal{O}(1) time, summing nums costs us \mathcal{O}(n) time, so the algorithm is overall linear. Because we have no information about which number is missing, an adversary could always design an input for which any algorithm that examines fewer than n numbers fails. Therefore, this solution is asymptotically optimal.
Space complexity : \mathcal{O}(1)

This approach only pushes a few integers around, so it has constant memory usage.