Math - Top Interview Questions[EASY] (8/9) - Python
Math
Most of the math questions asked in interviews do not require math knowledge beyond middle school level.
We recommend:
Count Primes
Power of Three.
412. Fizz Buzz
leetcode.com/problems/fizz-buzz/
피즈버즈 하나 가지고도 이런 다양한 토론을 할수 있군..
Solution
You must have played FizzBuzz as kids. FizzBuzz charm never gets old. And so here we are looking at how you can take on one step at a time and impress your interviewer with a better and neat approach to solve this problem.
Approach 1: Naive Approach
Intuition
The moment you hear of FizzBuzz you think whether the number is divisible by 3, 5 or both.
Algorithm
- Initialize an empty answer list.
- Iterate on the numbers from 1 ... N1...N.
- For every number, if it is divisible by both 3 and 5, add FizzBuzz to the answer list.
- Else, Check if the number is divisible by 3, add Fizz.
- Else, Check if the number is divisible by 5, add Buzz.
- Else, add the number.
Complexity Analysis
- Time Complexity: O(N)O(N)
- Space Complexity: O(1)O(1)
Approach 2: String Concatenation
Intuition
This approach won't reduce the asymptotic complexity, but proves to be a neater solution when FizzBuzz comes with a twist. What if FizzBuzz is now FizzBuzzJazz i.e.
3 ---> "Fizz" , 5 ---> "Buzz", 7 ---> "Jazz"
If you try to solve this with the previous approach the program would have too many conditions to check:
- Divisible by 3
- Divisible by 5
- Divisible by 7
- Divisible by 3 and 5
- Divisible by 3 and 7
- Divisible by 7 and 3
- Divisible by 3 and 5 and 7
- Not divisible by 3 or 5 or 7.
This way if the FizzBuzz mappings increase, the conditions would grow exponentially in your program.
Algorithm
Instead of checking for every combination of these conditions, check for divisibility by given numbers i.e. 3, 5 as given in the problem. If the number is divisible, concatenate the corresponding string mapping Fizz or Buzz to the current answer string.
For eg. If we are checking for the number 15, the steps would be:
Condition 1: 15 % 3 == 0 , num_ans_str = "Fizz" Condition 2: 15 % 5 == 0 , num_ans_str += "Buzz" => num_ans_str = "FizzBuzz"
So for FizzBuzz we just check for two conditions instead of three conditions as in the first approach.
Similarly, for FizzBuzzJazz now we would just have three conditions to check for divisibility.
class Solution {
public List<String> fizzBuzz(int n) {
// ans list
List<String> ans = new ArrayList<String>();
for (int num = 1; num <= n; num++) {
boolean divisibleBy3 = (num % 3 == 0);
boolean divisibleBy5 = (num % 5 == 0);
String numAnsStr = "";
if (divisibleBy3) {
// Divides by 3, add Fizz
numAnsStr += "Fizz";
}
if (divisibleBy5) {
// Divides by 5, add Buzz
numAnsStr += "Buzz";
}
if (numAnsStr.equals("")) {
// Not divisible by 3 or 5, add the number
numAnsStr += Integer.toString(num);
}
// Append the current answer str to the ans list
ans.add(numAnsStr);
}
return ans;
}
}
Complexity Analysis
- Time Complexity: O(N)O(N)
- Space Complexity: O(1)O(1)
Approach 3: Hash it!
Intuition
This approach is an optimization over approach 2. When the number of mappings are limited, approach 2 looks good. But what if you face a tricky interviewer and he decides to add too many mappings?
Having a condition for every mapping is not feasible or may be we can say the code might get ugly and tough to maintain.
What if tomorrow we have to change a mapping or may be delete a mapping? Are we going to change the code every time we have a modification in the mappings?
We don't have to. We can put all these mappings in a Hash Table.
Algorithm
- Put all the mappings in a hash table. The hash table fizzBuzzHash would look something like { 3: 'Fizz', 5: 'Buzz' }
- Iterate on the numbers from 1 ... N1...N.
- For every number, iterate over the fizzBuzzHash keys and check for divisibility.
- If the number is divisible by the key, concatenate the corresponding hash value to the answer string for current number. We do this for every entry in the hash table.
- Add the answer string to the answer list.
This way you can add/delete mappings to/from to the hash table and not worry about changing the code.
So, for FizzBuzzJazz the hash table would look something like { 3: 'Fizz', 5: 'Buzz', 7: 'Jazz' }
class Solution {
public List<String> fizzBuzz(int n) {
// ans list
List<String> ans = new ArrayList<String>();
// Hash map to store all fizzbuzz mappings.
HashMap<Integer, String> fizzBizzDict =
new HashMap<Integer, String>() {
{
put(3, "Fizz");
put(5, "Buzz");
}
};
for (int num = 1; num <= n; num++) {
String numAnsStr = "";
for (Integer key : fizzBizzDict.keySet()) {
// If the num is divisible by key,
// then add the corresponding string mapping to current numAnsStr
if (num % key == 0) {
numAnsStr += fizzBizzDict.get(key);
}
}
if (numAnsStr.equals("")) {
// Not divisible by 3 or 5, add the number
numAnsStr += Integer.toString(num);
}
// Append the current answer str to the ans list
ans.add(numAnsStr);
}
return ans;
}
}
Complexity Analysis
- Time Complexity : O(N)O(N)
- Space Complexity : O(1)O(1)
204. Count Primes
leetcode.com/problems/count-primes/
Easy
2503686Add to ListShare
Count the number of prime numbers less than a non-negative number, n.
Example 1:
Input: n = 10 Output: 4 Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
Example 2:
Input: n = 0 Output: 0
Example 3:
Input: n = 1 Output: 0
Constraints:
- 0 <= n <= 5 * 106
Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better?
Hide Hint 2
As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better?
Hide Hint 3
Let's write down all of 12's factors:
2 × 6 = 12 3 × 4 = 12 4 × 3 = 12 6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) { int count = 0; for (int i = 1; i < n; i++) { if (isPrime(i)) count++; } return count; } private boolean isPrime(int num) { if (num <= 1) return false; // Loop's ending condition is i * i <= num instead of i <= sqrt(num) // to avoid repeatedly calling an expensive function sqrt(). for (int i = 2; i * i <= num; i++) { if (num % i == 0) return false; } return true; }
Hide Hint 4
The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
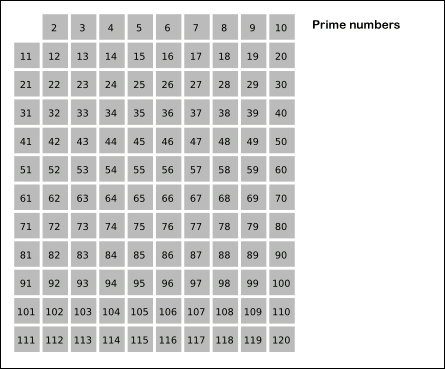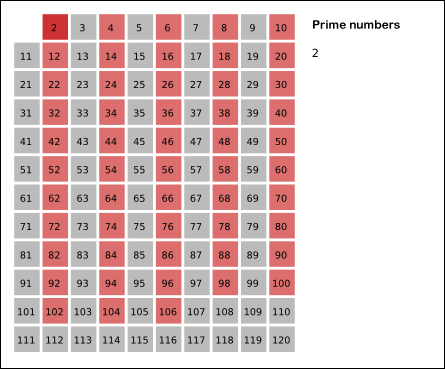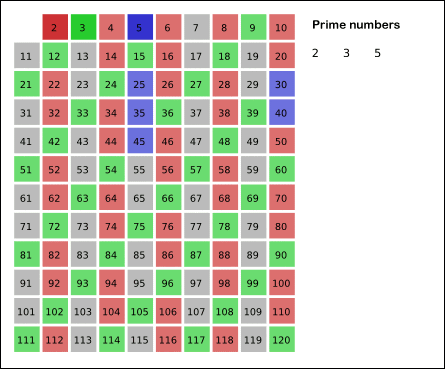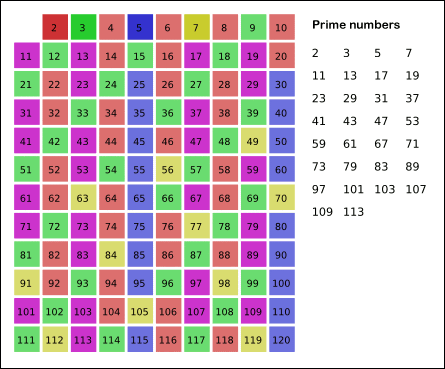
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well?
Hide Hint 5
4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off?
Hide Hint 6
In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition?
Hide Hint 7
It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3?
Hide Hint 8
Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
326. Power of Three
leetcode.com/problems/power-of-three/solution/
Given an integer n, return true if it is a power of three. Otherwise, return false.
An integer n is a power of three, if there exists an integer x such that n == 3x.
Example 1:
Input: n = 27 Output: true
Example 2:
Input: n = 0 Output: false
Example 3:
Input: n = 9 Output: true
Example 4:
Input: n = 45 Output: false
Constraints:
- -231 <= n <= 231 - 1
Follow up: Could you do it without using any loop / recursion?
Solution
In this article we will look into ways of speeding up simple computations and why that is useful in practice.
Approach 1: Loop Iteration
One simple way of finding out if a number n is a power of a number b is to keep dividing n by b as long as the remainder is 0. This is because we can write
\begin{aligned} n &= b^x \\ n &= b \times b \times \ldots \times b \end{aligned}nn=bx=b×b×…×b
Hence it should be possible to divide n by b x times, every time with a remainder of 0 and the end result to be 1.
Notice that we need a guard to check that n != 0, otherwise the while loop will never finish. For negative numbers, the algorithm does not make sense, so we will include this guard as well.
class Solution:
def isPowerOfThree(self, n: int) -> bool:
if n < 1:
return False
while n % 3 == 0:
n /= 3
return n == 1
Complexity Analysis
-
Time complexity : O(\log_b(n))O(logb(n)). In our case that is O(\log_3n)O(log3n). The number of divisions is given by that logarithm.
-
Space complexity : O(1)O(1). We are not using any additional memory.
Approach 2: Base Conversion
In Base 10, all powers of 10 start with the digit 1 and then are followed only by 0 (e.g. 10, 100, 1000). This is true for other bases and their respective powers. For instance in base 2, the representations of 10_2102, 100_21002 and 1000_210002 are 2_{10}210, 4_{10}410 and 8_{10}810 respectively. Therefore if we convert our number to base 3 and the representation is of the form 100...0, then the number is a power of 3.
Proof
Given the base 3 representation of a number as the array s, with the least significant digit on index 0, the formula for converting from base 3 to base 10 is:
\sum_{i=0}^{len(s) - 1} s[i] * 3^{i}∑i=0len(s)−1s[i]∗3i
Therefore, having just one digit of 1 and everything else 0 means the number is a power of 3.
Implementation
All we need to do is convert [1] the number to base 3 and check if it is written as a leading 1 followed by all 0.
A couple of built-in Java functions will help us along the way.
The code above converts number into base base and returns the result as a String. For example, Integer.toString(5, 2) == "101" and Integer.toString(5, 3) == "12".
The code above checks if a certain Regular Expression [2] pattern exists inside a string. For instance the above will return true if the substring "123" exists inside the string myString.
We will use the regular expression above for checking if the string starts with 1 ^1, is followed by zero or more 0s 0* and contains nothing else $.
Complexity Analysis
-
Time complexity : O(\log_3n)O(log3n).
Assumptions:
- Integer.toString() - Base conversion is generally implemented as a repeated division. The complexity of should be similar to our Approach 1: O(\log_3n)O(log3n).
- String.matches() - Method iterates over the entire string. The number of digits in the base 3 representation of n is O(\log_3n)O(log3n).
-
Space complexity : O(\log_3n)O(log3n).
We are using two additional variables,
- The string of the base 3 representation of the number (size \log_3nlog3n)
- The string of the regular expression (constant size)
Approach 3: Mathematics
We can use mathematics as follows
n = 3^i \\ i = \log_3(n) \\ i = \frac{\log_b(n)}{\log_b(3)}n=3ii=log3(n)i=logb(3)logb(n)
n is a power of three if and only if i is an integer. In Java, we check if a number is an integer by taking the decimal part (using % 1) and checking if it is 0.
Common pitfalls
This solution is problematic because we start using doubles, which means we are subject to precision errors. This means, we should never use == when comparing doubles. That is because the result of Math.log10(n) / Math.log10(3) could be 5.0000001 or 4.9999999. This effect can be observed by using the function Math.log() instead of Math.log10().
In order to fix that, we need to compare the result against an epsilon.
Complexity Analysis
-
Time complexity : UnknownUnknown The expensive operation here is Math.log, which upper bounds the time complexity of our algorithm. The implementation is dependent on the language we are using and the compiler [3]
-
Space complexity : O(1)O(1). We are not using any additional memory. The epsilon variable can be inlined.
Approach 4: Integer Limitations
An important piece of information can be deduced from the function signature
In particular, n is of type int. In Java, this means it is a 4 byte, signed integer [ref]. The maximum value of this data type is 2147483647. Three ways of calculating this value are
- System.out.println(Integer.MAX_VALUE);
- MaxInt = \frac{ 2^{32} }{2} - 12232−1 since we use 32 bits to represent the number, half of the range is used for negative numbers and 0 is part of the positive numbers
Knowing the limitation of n, we can now deduce that the maximum value of n that is also a power of three is 1162261467. We calculate this as:
3^{\lfloor{}\log_3{MaxInt}\rfloor{}} = 3^{\lfloor{}19.56\rfloor{}} = 3^{19} = 11622614673⌊log3MaxInt⌋=3⌊19.56⌋=319=1162261467
Therefore, the possible values of n where we should return true are 3^030, 3^131 ... 3^{19}319. Since 3 is a prime number, the only divisors of 3^{19}319 are 3^030, 3^131 ... 3^{19}319, therefore all we need to do is divide 3^{19}319 by n. A remainder of 0 means n is a divisor of 3^{19}319 and therefore a power of three.
Complexity Analysis
-
Time complexity : O(1)O(1). We are only doing one operation.
-
Space complexity : O(1)O(1). We are not using any additional memory.
Performance Measurements
Single runs of the function make it is hard to accurately measure the difference of the two solutions. On LeetCode, on the Accepted Solutions Runtime Distribution page, all solutions being between 15 ms and 20 ms. For completeness, we have proposed the following benchmark to see how the two solutions differ.
Java Benchmark Code
In the table below, the values are in seconds.
Iterations10^610610^710710^810810^9109MaxintMaxint
| Java Approach 1: (Naive) | 0.04 | 0.07 | 0.30 | 2.47 | 5.26 |
| Java Approach 2: (Strings) | 0.68 | 4.02 | 38.90 | 409.16 | 893.89 |
| Java Approach 3: (Logarithms) | 0.09 | 0.50 | 4.59 | 45.53 | 97.50 |
| Java Approach 4: (Fast) | 0.04 | 0.06 | 0.08 | 0.41 | 0.78 |
As we can see, for small values of N, the difference is not noticeable, but as we do more iterations and the values of n passed to isPowerOfThree() grow, we see significant boosts in performance for Approach 4.
Conclusion
Simple optimizations like this might seem negligible, but historically, when computation power was an issue, it allowed certain computer programs (such as Quake 3 [4]) possible.
References
관련 문제: 231. Power of Two
leetcode.com/problems/power-of-two/
구글기출
class Solution:
def isPowerOfTwo(self, n: int) -> bool:
if n == 0:
return False
while n % 2 == 0:
n /= 2
return n == 1Instead, the problem will be solved in \mathcal{O}(1)O(1) time with the help of bitwise operators. The idea is to discuss such bitwise tricks as
-
How to get / isolate the rightmost 1-bit : x & (-x).
-
How to turn off (= set to 0) the rightmost 1-bit : x & (x - 1).
These tricks are often used as something obvious in more complex bit-manipulation solutions, like for N Queens problem, and it's important to recognize them to understand what is going on.
Approach 1: Bitwise Operators : Get the Rightmost 1-bit

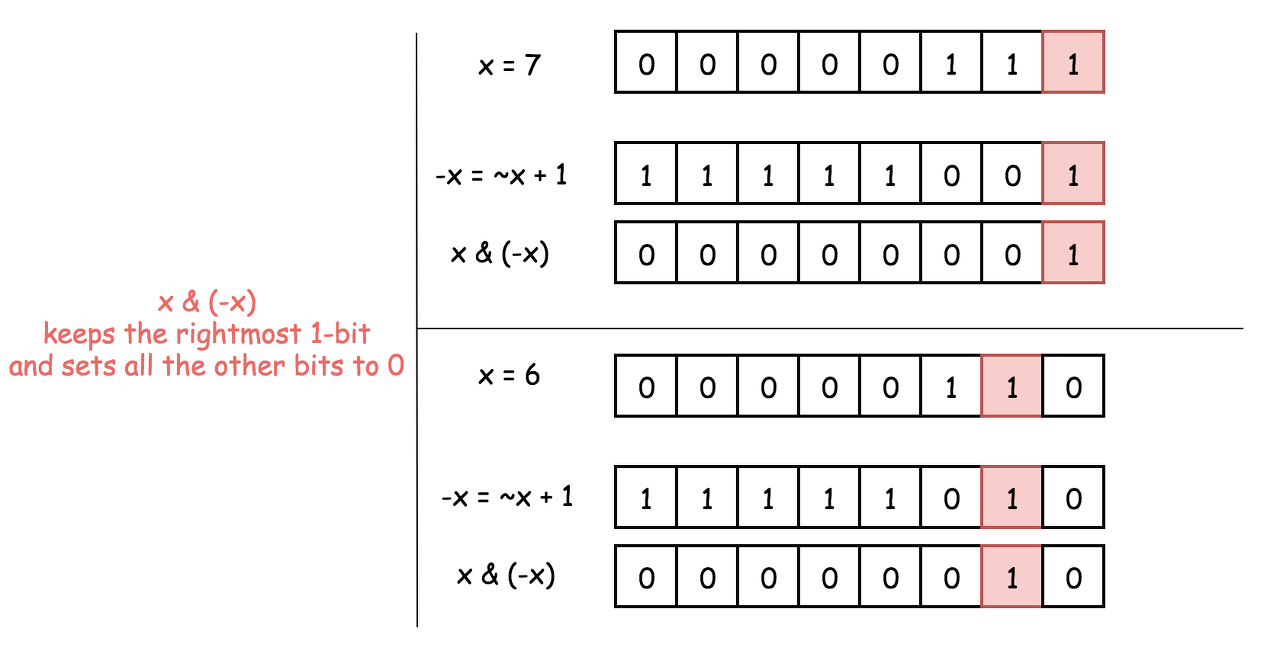
class Solution:
def isPowerOfTwo(self, n: int) -> bool:
if n == 0:
return False
return n & (-n) == n
Approach 2: Bitwise operators : Turn off the Rightmost 1-bit


leetcode.com/problems/power-of-four/
%4 하고 /4 하는거가 첫번째 어프로치
class Powers:
def __init__(self):
max_power = 15
self.nums = nums = [1] * (max_power + 1)
for i in range(1, max_power + 1):
nums[i] = 4 * nums[i - 1]
class Solution:
p = Powers()
def isPowerOfFour(self, n: int) -> bool:
return n in self.p.numsComplexity Analysis
-
Time complexity: \mathcal{O}(1)O(1).
-
Space complexity: \mathcal{O}(1)O(1).
from math import log2
class Solution:
def isPowerOfFour(self, n: int) -> bool:
return n > 0 and log2(n) % 2 == 0Complexity Analysis
-
Time complexity : \mathcal{O}(1)O(1).
-
Space complexity : \mathcal{O}(1)O(1).
Approach 3: Bit Manipulation
Let's first check if num is a power of two: x > 0 and x & (x - 1) == 0.
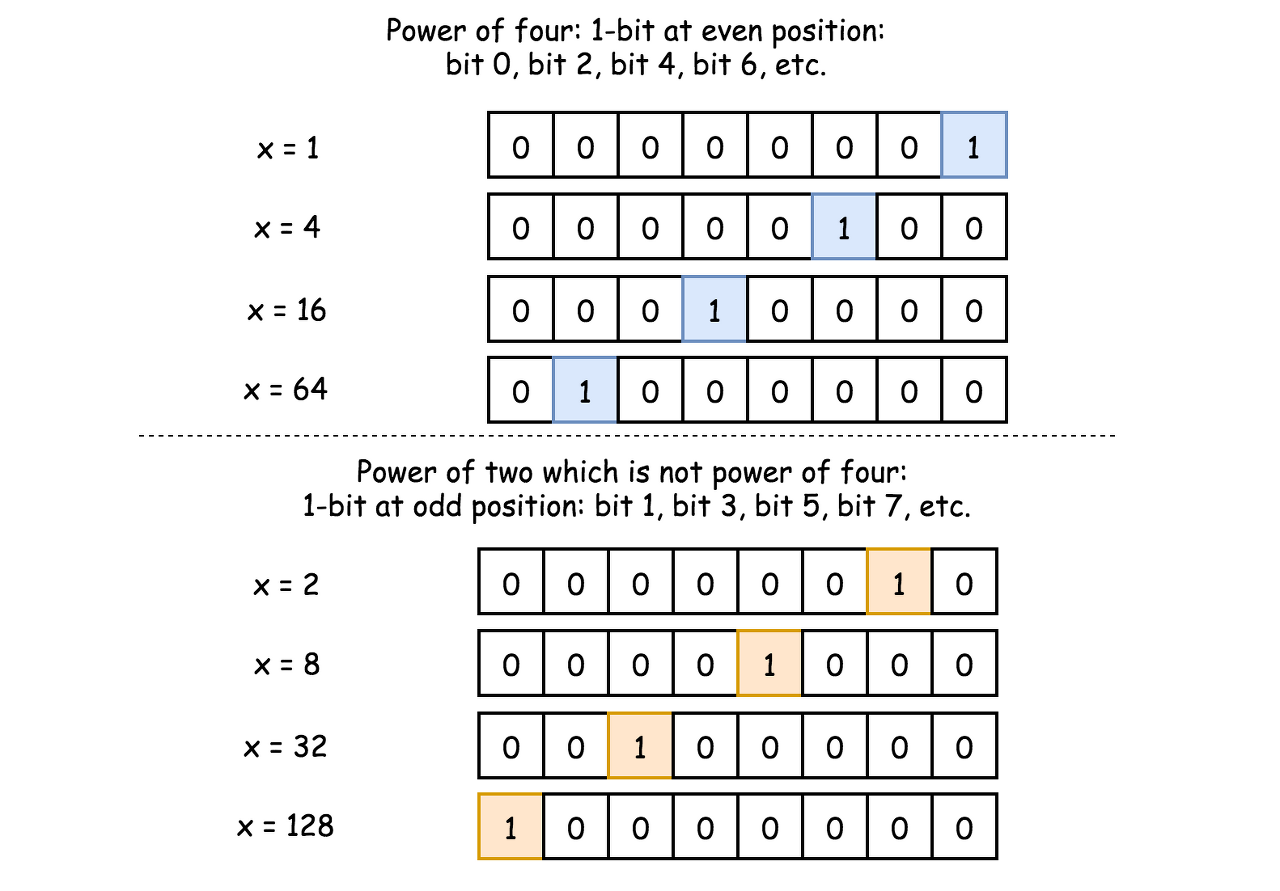
Hence power of four would make a zero in a bitwise AND with number (101010...10)_2(101010...10)2:
4^a \land (101010...10)_2 == 04a∧(101010...10)2==0
How long should be (101010...10)_2(101010...10)2 if xx is a signed integer? 32 bits. To write shorter, in 8 charaters instead of 32, it's common to use hexadecimal representation: (101010...10)_2 = (aaaaaaaa)_{16}(101010...10)2=(aaaaaaaa)16.
x \land (aaaaaaaa)_{16} == 0x∧(aaaaaaaa)16==0
class Solution:
def isPowerOfFour(self, num: int) -> bool:
return num > 0 and num & (num - 1) == 0 and num & 0xaaaaaaaa == 0
Approach 4: Bit Manipulation + Math
If xx is a power of two and x % 3 == 1, then xx is a power of four.
class Solution:
def isPowerOfFour(self, num: int) -> bool:
return num > 0 and num & (num - 1) == 0 and num % 3 == 1
13. Roman to Integer
leetcode.com/problems/roman-to-integer/
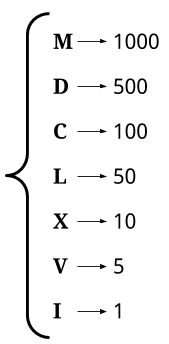
Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.Symbol Value I 1 V 5 X 10 L 50 C 100 D 500 M 1000
For example, 2 is written as II in Roman numeral, just two one's added together. 12 is written as XII, which is simply X + II. The number 27 is written as XXVII, which is XX + V + II.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:
- I can be placed before V (5) and X (10) to make 4 and 9.
- X can be placed before L (50) and C (100) to make 40 and 90.
- C can be placed before D (500) and M (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
Example 1:
Input: s = "III" Output: 3
Example 2:
Input: s = "IV" Output: 4
Example 3:
Input: s = "IX" Output: 9
Example 4:
Input: s = "LVIII" Output: 58 Explanation: L = 50, V= 5, III = 3.
Example 5:
Input: s = "MCMXCIV" Output: 1994 Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.
Constraints:
- 1 <= s.length <= 15
- s contains only the characters ('I', 'V', 'X', 'L', 'C', 'D', 'M').
- It is guaranteed that s is a valid roman numeral in the range [1, 3999]
* If I comes before V or X, subtract 1 eg: IV = 4 and IX = 9
* If X comes before L or C, subtract 10 eg: XL = 40 and XC = 90
* If C comes before D or M, subtract 100 eg: CD = 400 and CM = 900
Overview
In a lot of countries, Roman Numerals are taught in elementary school-level math. This has made them a somewhat popular "easy" interview question. Unfortunately though, this ignores the fact that not everybody learned them in school, and therefore a big advantage has been given to those who did. I suspect it's also difficult for a lot of us who have learned them previously to fully appreciate how much easier prior experience makes this question. While this is very unfair, and possibly very frustrating, keep in mind that the best thing you can do is work through this question and the related question Integer to Roman so that you don't get caught out by it in a real interview.
Can we assume the input is valid?
Yes. Here on Leetcode, you can make that assumption because you haven't been told what to do if it isn't.
In a real interview, this is a question you should ask the interviewer. Don't ever assume without asking in a real interview that the input has to be valid.
Is there only one valid representation for each number?
This is more relevant to the other question, Integer to Roman, however we'll still briefly look at it now.
Given that the representation for 3 is III, it could seem natural that the representation for 15 is VVV, because that would be 5 + 5 + 5. However, it's actually XV, which is 10 + 5. How are you even supposed to know which is correct?
The trick is to use the "biggest" symbols you can. Because X is bigger than V, we should use an X first and then make up the remainder with a single V, giving XV.
We'll talk more about this in the Integer to Roman article. This question is a lot simpler because there's only one logical way of converting from a Roman Numeral to an Integer. This is also why this question is labelled as "easy", whereas the other is labelled as "medium".
A few more examples
If you're not very familiar with Roman Numerals, work through these examples and then have another go at writing your own algorithm before reading the rest of this solution article.
What is CXVII as an integer?
Recall that C = 100, X = 10, V = 5, and I = 1. Because the symbols are ordered from most significant to least, we can simply add the symbols, i.e. C + X + V + I + I = 100 + 10 + 5 + 1 + 1 = 117.
What is DXCI as an integer?
Recall that D = 500.
Now, notice that this time the symbols are not ordered from most significant to least—the X and C are out of numeric order. Because of this, we subtract the value of X (10) from the value of C (100) to get 90.
So, going from left to right, we have D + (C - X) + I = 500 + 90 + 1 = 591.
What is CMXCIV as an integer?
Recall that M = 1000.
The symbols barely look sorted at all here—from left-to-right we have 100, 1000, 10, 100, 1, 5. Do not panic though, we just need to look for each occurrence of a smaller symbols preceding a bigger symbol. The first, third, and fifth symbols are all smaller than their next symbol. Therefore they are all going to be subtracted from their next.
- The first two symbols are CM. This is M - C = 1000 - 100 = 900
- The second two symbols are XC. This is C - X = 100 - 10 = 90.
- The final two symbols are IV. This is V - I = 5 - 1 = 4.
Like we did above, we add these together. (M - C) + (C - X) + (V - I) = 900 + 90 + 4 = 994.
Approach 1: Left-to-Right Pass
Intuition
Let's hard-code a mapping with the value of each symbol so that we can easily look them up.
Now, recall that each symbol adds its own value, except for when a smaller valued symbol is before a larger valued symbol. In those cases, instead of adding both symbols to the total, we need to subtract the large from the small, adding that instead.
Therefore, the simplest algorithm is to use a pointer to scan through the string, at each step deciding whether to add the current symbol and go forward 1 place, or add the difference of the next 2 symbols and go forward 2 places. Here is this algorithm in pseudocode.
total = 0 i = 0 while i < s.length: if at least 2 symbols remaining AND value of s[i] < value of s[i + 1]: total = total + (value of s[i + 1]) - (value of s[i]) i = i + 2 else: total = total + (value of s[i]) i = i + 1 return total
Here is an animation of the above algorithm.

1 / 10
Recall that the input is always valid. This means that we don't need to worry about being given inputs such as ICD.
Algorithm
Complexity Analysis
Let nn be the length of the input string (the total number of symbols in it).
-
Time complexity : O(1)O(1).
As there is a finite set of roman numerals, the maximum number possible number can be 3999, which in roman numerals is MMMCMXCIX. As such the time complexity is O(1)O(1).
If roman numerals had an arbitrary number of symbols, then the time complexity would be proportional to the length of the input, i.e. O(n)O(n). This is assuming that looking up the value of each symbol is O(1)O(1).
-
Space complexity : O(1)O(1).
Because only a constant number of single-value variables are used, the space complexity is O(1)O(1).
Approach 2: Left-to-Right Pass Improved
Intuition
Instead of viewing a Roman Numeral as having 7 unique symbols, we could instead view it as having 13 unique symbols—some of length-1 and some of length-2.

For example, here is the Roman Numeral MMCMLXXXIX broken into its symbols using this definition:

We can then look up the value of each symbol and add them together.

After making a Map of String -> Integer with the 13 "symbols", we need to work our way down the string in the same way as before (we'll do left-to-right, however right-to-left will work okay too), firstly checking if we're at a length-2 symbol, and if not, then treating it as a length-1 symbol.
total = 0 i = 0 while i < s.length: if at least 2 characters remaining and s.substing(i, i + 1) is in values: total = total + (value of s.substring(i, i + 1)) i = i + 2 else: total = total + (value of s[i]) i = i + 1 return total
Here is an animation showing the algorithm.

1 / 8
Algorithm
Complexity Analysis
-
Time complexity : O(1)O(1).
Same as Approach 1.
-
Space complexity : O(1)O(1).
Same as Approach 1.
Approach 3: Right-to-Left Pass
Intuition
This approach is a more elegant variant of Approach 1. Just to be clear though, Approach 1 and Approach 2 are probably sufficient for an interview. This approach is still well worth understanding though.
In the "subtraction" cases, such as XC, we've been updating our running sum as follows:
sum += value(C) - value(X)
However, notice that this is mathematically equivalent to the following:
sum += value(C) sum -= value(X)
Utilizing this means that we can process one symbol each time we go around the main loop. We still need to determine whether or not our current symbol should be added or subtracted by looking at the neighbour though.
In Approach 1, we had to be careful when inspecting the next symbol to not go over the end of the string. This check wasn't difficult to do, but it increased the code complexity a bit, and it turns out we can avoid it with this approach!
Observe the following:
- Without looking at the next symbol, we don't know whether or not the left-most symbol should be added or subtracted.
- The right-most symbol is always added. It is either by itself, or the additive part of a pair.
So, what we can do is initialise sum to be the value of the right-most (last) symbol. Then, we work backwards through the string, starting from the second-to-last-symbol. We check the symbol after (i + 1) to determine whether the current symbol should be "added" or "subtracted".
last = s.length - 1 total = value(last) ` for i from last - 1 down to 0: if value(s[i]) < value(s[i+1]): total -= value(s[i]) else: total += value(s[i]) return sum
Because we're starting at the second-to-last-index, we know that index i + 1 always exists. We no longer need to handle its potential non-existence as a special case, and additionally we're able to (cleanly) use a for loop, as we're always moving along by 1 index at at time, unlike before where it could have been 1 or 2.
Here is an animation of the above approach.

1 / 9
Algorithm
values = {
'I': 1,
'V': 5,
'X': 10,
'L': 50,
'C': 100,
'D': 500,
'M': 1000
}
class Solution:
def romanToInt(self, s: str) -> int:
total = values.get(s[-1])
for i in reversed(range(len(s)-1)):
if values[s[i]] < values[s[i+1]]:
total -= values[s[i]]
else:
total += values[s[i]]
return total
Complexity Analysis
-
Time complexity : O(1)O(1).
Same as Approach 1.
-
Space complexity : O(1)O(1).
Same as Approach 1.
Array - Top Interview Questions[EASY] (1/9) : Java
String - Top Interview Questions[EASY] (2/9) : Java
Linked List - Top Interview Questions[EASY] (3/9) : Java
Trees - Top Interview Questions[EASY] (4/9) : Java
Sorting and Searching - Top Interview Questions[EASY] (5/9) : Java
Dynamic Programming - Top Interview Questions[EASY] (6/9) : Java
Design - Top Interview Questions[EASY] (7/9) - Java
Array - Top Interview Questions[EASY] (1/9) : Python
String - Top Interview Questions[EASY] (2/9) : Python
Linked List - Top Interview Questions[EASY] (3/9) : Python
Trees - Top Interview Questions[EASY] (4/9) : Python
Sorting and Searching - Top Interview Questions[EASY] (5/9) : Python
Dynamic Programming - Top Interview Questions[EASY] (6/9) : Python
Design - Top Interview Questions[EASY] (7/9) - Python





