딥러닝 101 - 무료 강의 전체 소개 | Deep Learning 101
딥러닝 101 재생목록은 CNN부터 트랜스포머, VAE, ResNet까지 현대 딥러닝의 핵심 개념을 한 번에 훑을 수 있는 입문·중급용 강의 시리즈입니다. 실습 위주의 설명과 직관적인 비유가 많아서, 수식에 압도되지 않고도 개념을 체계적으로 정리하고 싶은 학습자에게 특히 유용한 구성입니다.

유투브 재생 목록
https://youtube.com/playlist?list=PLW2RwdZfXkE-Bn1dlwYr7YxBcl7vWyrmq&si=Rv8-rYyIic9NyOku
강의 구성의 특징
이 재생목록은 총 25개의 영상으로 구성되어 있으며, 합성곱신경망(CNN), 순환신경망(RNN), LSTM, 오토인코더, GAN, Word2Vec, Seq2Seq, 어텐션, 트랜스포머, VAE, ResNet 등 대표적인 딥러닝 모델들을 일관된 흐름 속에서 다룹니다. 각 영상은 개념 소개 → 직관적 예시 설명 → 간단한 수식 정리 → 코드 구현(또는 구현 아이디어) 순서로 전개되어, 이론과 실습을 자연스럽게 연결해 주는 구조입니다.
다루는 주요 주제들
재생목록의 초반부에서는 합성곱신경망과 나만의 CNN 만들기, RNN과 한글 텍스트를 활용한 RNN 구현 등, 시각·시계열 데이터를 다루는 기본 아키텍처에 집중합니다. 이어서 LSTM, Cross Entropy, 확률적 경사하강법, L1/L2 정규화 등 모델 학습과 일반화에 필수적인 수학·최적화 개념을 짚어 주어, 이후 심화 모델을 이해할 토대를 만들어 줍니다.
중반부에는 오토인코더와 GAN, Word2Vec, KL Divergence 등을 통해 표현 학습과 생성 모델, 분포 간 거리 개념까지 폭넓게 다룹니다. 이 구간은 “표현을 어떻게 잘 학습하고, 그 표현을 바탕으로 새로운 데이터를 어떻게 만들어내는가”에 초점을 둔 구성이라, 생성 모델에 관심 있는 학습자에게 상당히 매력적입니다.
후반부에서는 Seq2Seq, 어텐션, Seq2Seq+어텐션, 트랜스포머, 트랜스포머 기반 챗봇, VAE 및 ResNet까지 자연어 처리와 딥 제너레이티브 모델, 딥 네트워크 학습 안정화라는 세 가지 축을 한 번에 다룹니다. 특히 “트랜스포머, 스텝 바이 스텝”과 “트랜스포머로 (또) 챗봇 만들기”는 최근 LLM 구조를 직관적으로 이해하는 데 좋은 디딤돌이 되는 파트입니다.
학습 난이도와 적합한 대상
수준은 “완전 입문자”보다는, 기본적인 미분·행렬 연산과 파이썬 또는 PyTorch 사용 경험이 어느 정도 있는 학습자에게 잘 맞는 정도입니다. 각 영상이 개별 주제를 독립적으로 다루기 때문에, CNN·RNN·트랜스포머처럼 관심 있는 토픽만 골라 들어도 흐름을 이해하는 데 무리가 없도록 구성되어 있습니다.
반면, 수학적 세부 증명보다는 직관과 구현에 초점이 맞춰져 있어, 이론을 엄밀하게 파고들고 싶은 전통 수학 전공자에게는 약간 가볍게 느껴질 수 있습니다. 대신, “딥러닝 이론을 연구 논문 수준이 아니라, 실전 구현과 응용 중심으로 빠르게 정리하고 싶은 공대·전산 계열 학생”에게는 부담과 효용의 균형이 좋은 편입니다.
관련 강의
선행 과정으로 아래의 과목들을 선 이수 하시는것을 추천합니다.
[AI 인공지능 머신러닝 딥러닝/인공지능 수학] - 2025 인공지능·머신러닝 입문자를 위한 핵심 통계개념 완전정복 (1/2)
2025 인공지능·머신러닝 입문자를 위한 핵심 통계개념 완전정복 (1/2)
안녕하세요! 오늘은 최근에 시청한 유튜브 신박Ai의 “[인공지능을 위한 머신러닝101] 머신러닝을 위한 기초통계개념” 영상을 바탕으로, 인공지능과 머신러닝을 공부하는 데 꼭 필요한 통계 개
inner-game.tistory.com
[AI 인공지능 머신러닝 딥러닝] - 인공지능 딥러닝 기초 완전정복: 유튜브로 배우는 신경망·딥러닝·실습코딩 가이드 | 인공신경망기초
인공지능 딥러닝 기초 완전정복: 유튜브로 배우는 신경망·딥러닝·실습코딩 가이드 | 인공신경
안녕하세요! 오늘은 제가 최근에 시청한 유튜브 플레이리스트 “인공신경망기초-신박Ai”를 바탕으로, 인공지능(Artificial Intelligence; AI) 기초에 대해 공부한 내용을 정리하여 티스토리 블로그 포
inner-game.tistory.com
활용 팁과 후기
이 재생목록을 가장 효율적으로 활용하는 방법은, 강의를 한 번 쭉 시청하면서 개념 지도를 만든 뒤, 관심 있는 파트(CNN, GAN, 트랜스포머, VAE 등)를 선택해 직접 코드를 따라 치며 두 번째 회독을 하는 방식입니다. 특히 “나만의 CNN/RNN 만들기”, “오토인코더 PyTorch 구현”, “GAN/Seq2Seq/트랜스포머로 챗봇 만들기”, “VAE를 만들어보자” 같은 구현 중심 영상은 개인 프로젝트의 출발점으로 삼기 좋습니다.
종합하면, 딥러닝의 대표 모델들을 한 코스 안에서 연결해서 이해하고 싶은 대학·대학원생, 현업 개발자, 자율학습자에게 추천할 만한 강의 시리즈입니다. 기초를 어느 정도 닦은 뒤 이 재생목록을 순서대로 수강하면, 최근 딥러닝 트렌드를 따라가고 논문을 읽을 때 필요한 어휘와 직관을 단단하게 다질 수 있을 것입니다.
강의 목차
1강. [Deep Learning 101] 합성곱신경망 CNN, Convolutional Neural Network
이 영상은 합성곱신경망(CNN)의 직관적 구조와 동작 원리를 예제와 함께 차분하게 설명해 주는 입문 강의이다. 이미지가 픽셀 격자로 이루어진 데이터라는 아주 기초적인 수준에서 출발해, 합성곱 연산과 커널, 스트라이드, 풀링, 마지막의 밀집층까지 CNN의 전형적인 구성요소를 한 번에 훑어볼 수 있다.
강의 개요와 구성
· 강의는 먼저 이미지가 가진 공간적 구조를 짚으면서, 왜 일반적인 완전연결 신경망보다 CNN이 이미지 처리에 적합한지 자연스럽게 문제의식을 던진다.
· 이어서 합성곱 층, 풀링 층, 밀집층(fully-connected layer)이라는 세 가지 기본 블록을 소개하고, 이 블록들이 어떻게 연결되어 이미지 분류 모델을 이루는지 큰 그림을 제시한다.
· 후반부에는 CNN의 학습 과정과 인간 시각 피질(V1, V2, IT 등)의 계층적 처리 구조를 비교하며, CNN이 어디까지나 영감을 받은 모델이라는 점도 짚어 준다.
합성곱 연산과 커널의 직관
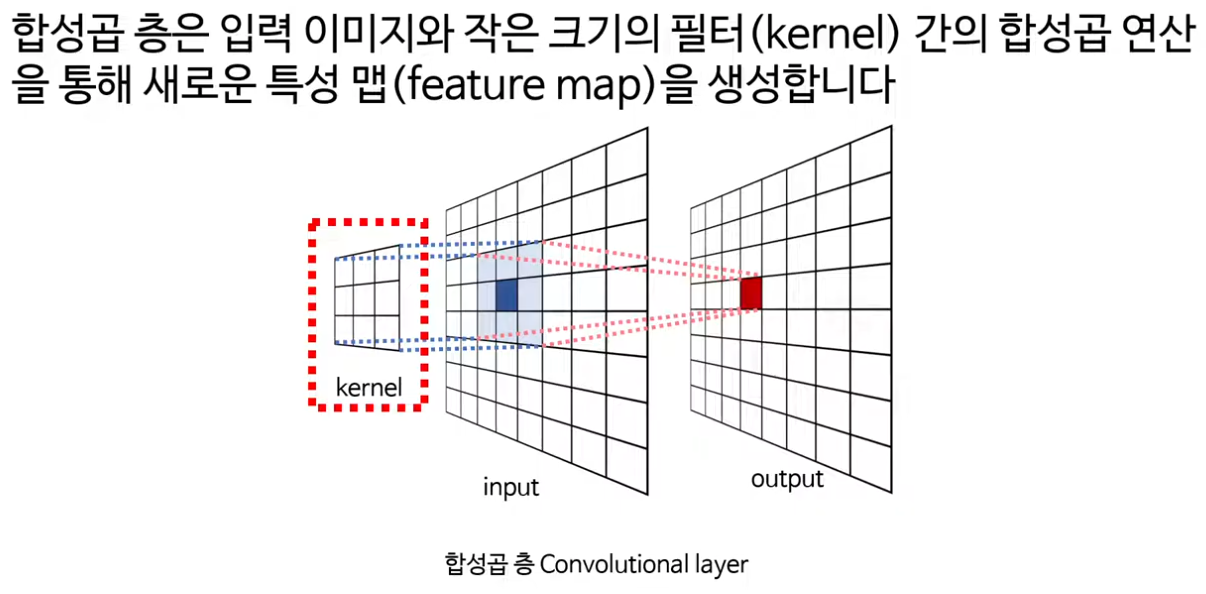
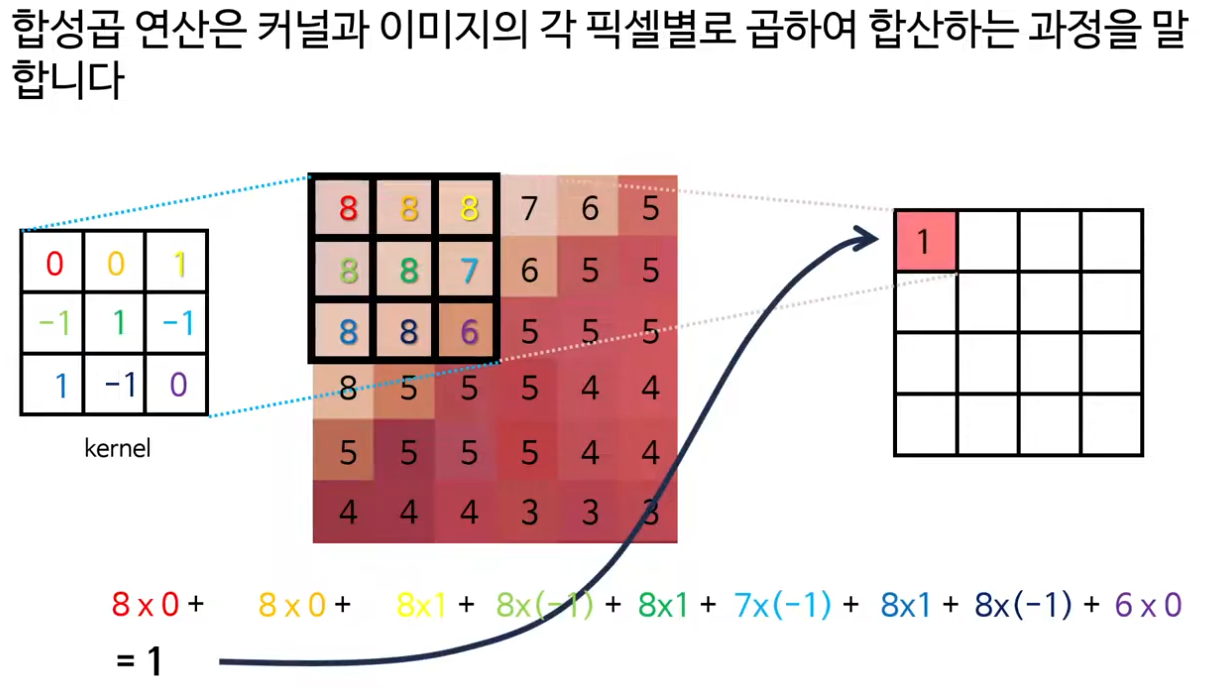
· 강의의 중심은 합성곱 층에 있고, 작은 행렬인 커널(필터)을 이미지 위로 슬라이딩 하며 각 위치에서 요소별 곱과 합을 계산해 feature map을 만드는 과정을 구체적인 숫자 예제로 보여준다.
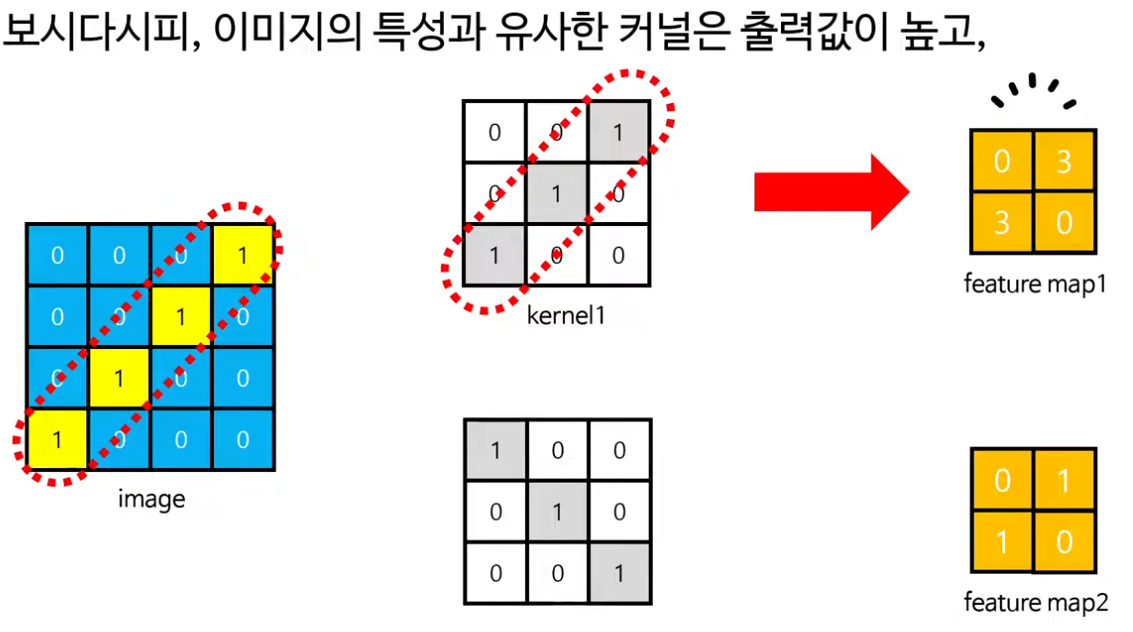
· 특히 “이미지의 특성과 유사한 커널일수록 출력값이 커지고, 그렇지 않으면 작아진다”는 설명을 통해, 커널이 결국 특정 패턴(직선, 곡선, 엣지 등)에 반응하는 탐지기라는 점을 직관적으로 이해하게 해 준다.
· 여러 종류의 커널을 두었을 때, 숫자 1 이미지에서는 직선 커널들이, 숫자 0 이미지에서는 곡선 커널들이 더 강하게 반응한다는 예시는 CNN이 “필터를 학습해서” 패턴을 골라낸다는 핵심 아이디어를 잘 전달한다.







커널 크기, 스트라이드, 연산량의 트레이드오프
· 강의에서는 커널의 크기가 feature map의 해상도, 즉 얼마나 세밀한 특징을 볼 수 있는지와 직결된다는 점을 강조한다.
· 픽셀 수와 feature map 크기가 커질수록 더 디테일한 정보를 다룰 수 있지만, 그만큼 연산량과 학습 시간이 폭발적으로 증가한다는 현실적인 제약도 함께 짚으면서, 적절한 커널 크기를 찾는 것이 모델링의 중요한 설계 포인트라고 이야기한다.
· 스트라이드(stride)에 대해서도, 1일 때는 한 칸씩, 2일 때는 두 칸씩 “건너뛰며” 움직이는 예시를 통해, 동일한 커널이라도 스트라이드 설정에 따라 feature map의 크기와 연산량이 크게 달라진다는 점을 시각적으로 보여준다.


풀링층의 역할과 효과
· 풀링층은 합성곱 층에서 나온 feature map의 공간적 크기를 줄이면서도 중요한 특징은 유지하는 역할을 한다고 설명한다.
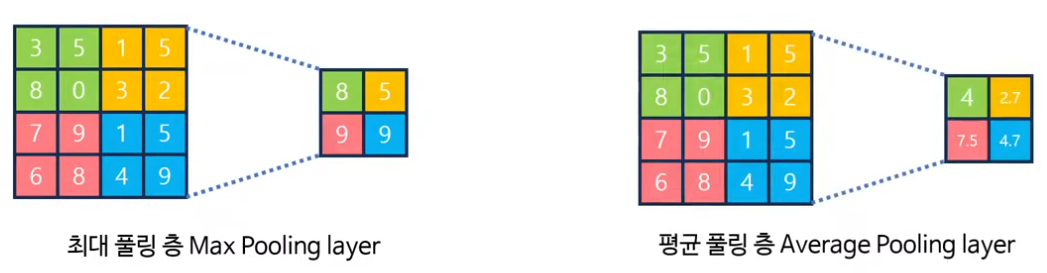
· 대표적으로 맥스 풀링과 평균 풀링을 소개하며, 4×4 행렬이 풀링을 거쳐 2×2로 줄어드는 예시를 통해 “차원을 줄이면서도 요지는 남긴다”는 감각을 잡을 수 있게 돕는다.
· 강의자는 풀링이 단순히 크기를 줄이는 차원을 넘어, 연산량 폭증을 막고 과적합을 완화하는 데도 기여한다는 점을 짚으면서, 왜 대부분의 CNN 구조에서 풀링이 중요한 구성요소로 자리 잡았는지 설명한다.

밀집층과 학습 과정, 그리고 시각 피질과의 비유
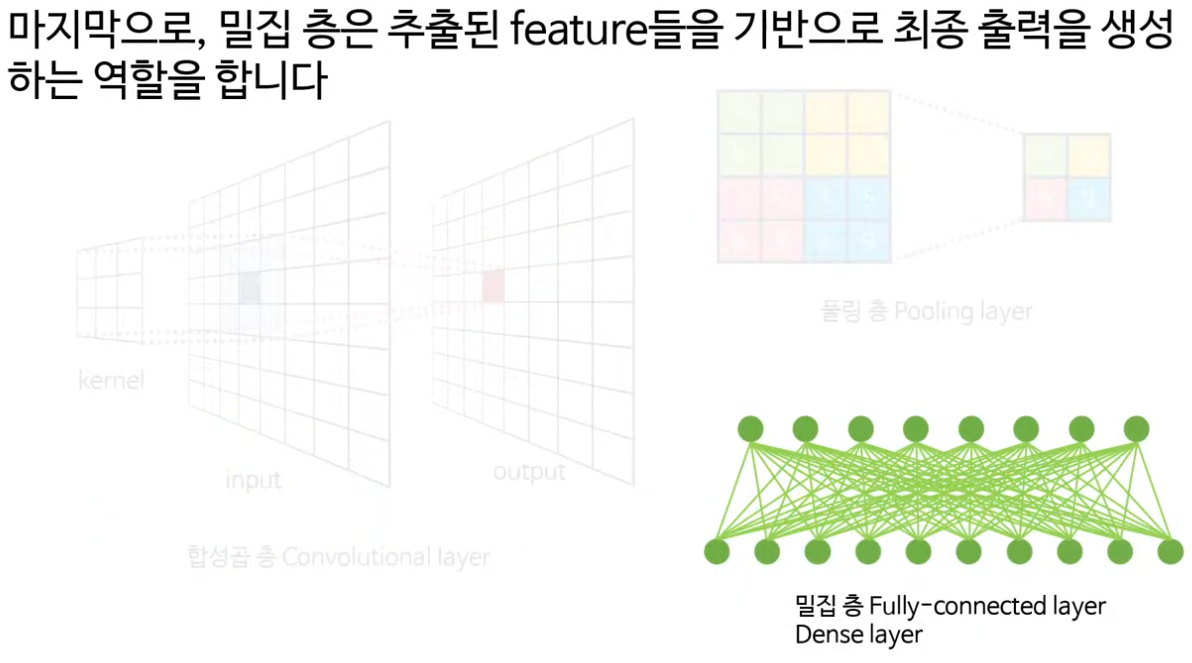
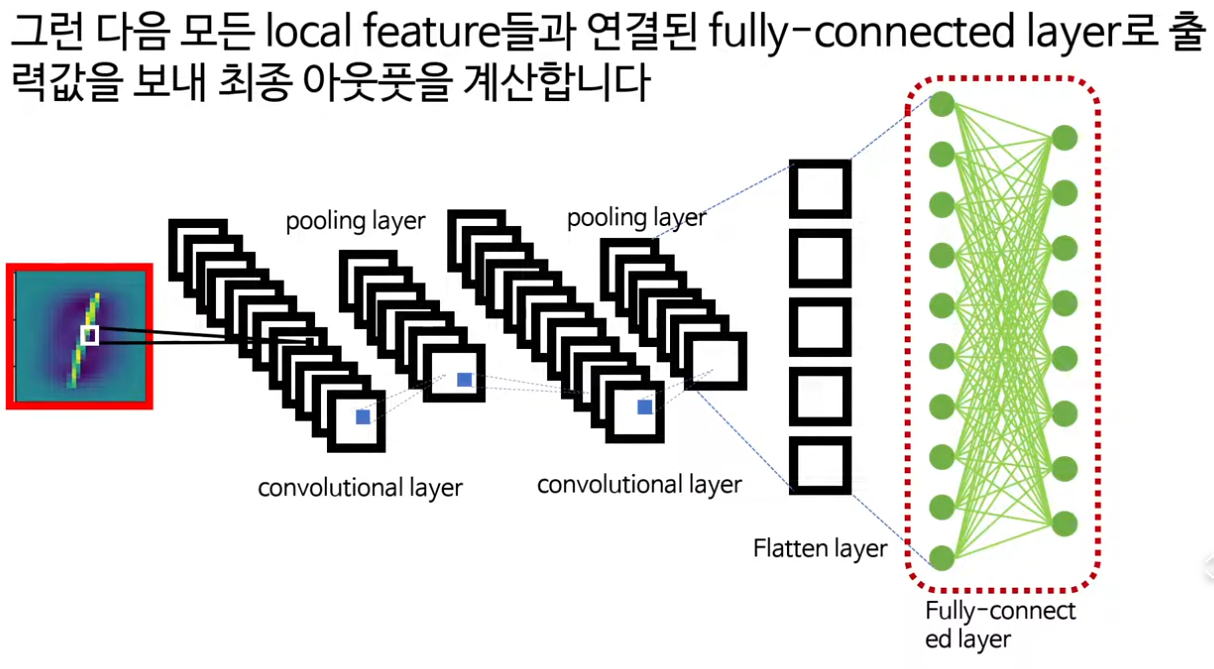
· 마지막 부분에서는 합성곱과 풀링으로 추출한 로컬 피처들을 flatten 한 뒤 fully-connected layer로 보내 최종 분류를 수행하는 과정을 설명한다.
· 여기서 로컬 피처의 출력값을 “일종의 확률”처럼 해석하며, 개·고양이 분류 예시를 통해 역전파와 경사하강법을 통해 커널 가중치가 점점 특정 클래스의 로컬 패턴에 더 잘 반응하도록 업데이트된다는 흐름을 잡아 준다.
· 끝으로 CNN과 인간 시각 피질의 계층 구조(V1에서 단순한 선, 상위 영역에서 복잡한 물체와 얼굴)를 나란히 놓고, 층이 깊어질수록 더 복잡한 피처를 처리한다는 공통된 방향성을 짚어 주면서 강의를 마무리한다.





이 영상은 수식보다 그림과 예제를 중심으로 설명하기 때문에, 처음 CNN을 접하는 입문자나 직관을 다시 정리하고 싶은 학습자에게 소개하기에 적합한 강의라 할 수 있다.
2강. [Deep Learning 101] 나만의 CNN을 만들어보자
not yet
3강. [Deep Learning 101] 순환신경망 RNN, Recurrent Neural Networks (수정본)
이 영상은 순환신경망 RNN의 개념부터 순전파·역전파(BPTT)까지, 수식과 숫자 예제를 통해 꽤 깊이 있게 파고드는 강의입니다. 시계열 데이터 처리의 직관과 함께 실제 계산 과정을 하나하나 따라가 보고 싶은 학습자에게 잘 맞는 구성입니다.
이 강의는 “RNN이 무엇인지 얼추 안다”에서 그치지 않고, 순전파와 역전파가 실제 숫자 수준에서 어떻게 돌아가는지 한 번쯤 끝까지 따라가 보고 싶은 학습자에게 특히 유익한 콘텐츠입니다. ChatGPT 같은 현대 언어모델의 이론적 뿌리가 되는 고전 RNN을 깊이 이해하고 싶다면, 정리해 두고 필요할 때마다 다시 꺼내 보기 좋은 레퍼런스로 삼을 만한 영상입니다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 3강. 순환신경망 RNN, Recurrent Neural Networks | Deep Learning 101
딥러닝 101 - 3강. 순환신경망 RNN, Recurrent Neural Networks | Deep Learning 101
3강. [Deep Learning 101] 순환신경망 RNN, Recurrent Neural Networks (수정본) 이 영상은 순환신경망 RNN의 개념부터 순전파·역전파(BPTT)까지, 수식과 숫자 예제를 통해 꽤 깊이 있게 파고드는 강의입니다. 시
inner-game.tistory.com
4강. [Deep Learning 101] 나만의 RNN을 만들어보자 (feat.훈민정음서문)
not yet
5강. [Deep Learning 101] LSTM, 초보자를 위한 안내서
이 영상은 LSTM이 등장하게 된 배경부터 구조·순전파·역전파 알고리즘까지, “왜 이렇게 설계됐는지”를 직관과 수식으로 함께 풀어 주는 이론 중심 강의입니다. 특히 RNN의 장기 의존성 문제와 LSTM의 셀 상태·게이트 메커니즘을 연결해 설명해 주기 때문에 입문자에게도 맥락이 잘 잡히는 구성입니다.
LSTM이 탄생한 배경: 장기 의존성 문제
강의는 먼저 기본 RNN의 역전파 수식을 다시 꺼내와, 시간 축이 길어질수록 체인 룰로 곱해지는 항들이 1보다 작은 값이라면 기울기가 0에 가까워지는 현상을 보여 줍니다. 이로 인해 문장 번역에서 “Don’t … underestimate your inner strength” 같은 문장에서, 의미상 짝을 이루는 “Don’t–마세요”처럼 멀리 떨어진 단어들 사이의 의존성이 잘 학습되지 않는다는 예시를 듭니다.
이렇게 시간적으로 먼 정보가 학습에 거의 기여하지 못하는 현상을 장기 의존성 문제라 부르고, 이를 해결하기 위한 RNN의 변형으로 LSTM(Long Short-Term Memory) 이 제안되었다는 역사적 맥락을 간단히 짚어 줍니다.
LSTM의 구조와 셀 상태의 역할
다음으로 강의는 LSTM의 핵심을 “셀 상태(cell state)와 네 개의 게이트”로 정리합니다. LSTM은 기본적으로 RNN처럼 시계열 데이터를 처리하지만, 내부에 장기 기억에 해당하는 셀 상태 C t C t 와 보다 단기적인 정보를 담는 은닉 상태 h t h t 두 흐름을 동시에 유지한다는 점이 강조됩니다.
· Forget 게이트: 이전 은닉 상태 h t − 1 h t−1 와 현재 입력 x t x t 를 concat한 벡터에 가중치 W f W f 를 곱하고 sigmoid를 취해, 0~1 사이의 값으로 “무엇을 얼마나 지울지”를 결정합니다. 이 값이 셀 상태 C t − 1 C t−1 와 원소별 곱(element-wise)으로 결합되며, 0에 가까운 위치의 정보는 잊혀지고 1에 가까운 위치의 정보는 유지됩니다.
· Input 게이트와 Candidate 게이트: Input 게이트는 forget 게이트와 동일하게 sigmoid를 통해 “무엇을 새로 쓸지”를 결정하고, Candidate 게이트는 tanh를 통해 − 1 −1과 1 사이의 후보 정보 C ~ t C ~ t 를 만듭니다. 두 출력의 원소별 곱을 통해 “현재 입력 중 기억할 부분”만 추려 셀 상태에 더해 장기 기억을 업데이트합니다.
· Output 게이트: 업데이트된 셀 상태 C t C t 를 tanh로 스케일링한 뒤, output 게이트의 sigmoid 출력과 원소별 곱을 해 새로운 은닉 상태 h t h t 를 만듭니다. 이 h t h t 는 셀 상태보다 더 단기적인 특성을 반영하며, 다음 시점의 입력이자 최종 출력층에 전달되는 특징 벡터로 사용됩니다.
이 과정을 통해 LSTM은 셀 상태에 비교적 장기적인 정보를, 은닉 상태에 단기적인 정보를 담으면서, RNN보다 훨씬 안정적으로 긴 시퀀스를 다룰 수 있는 구조를 갖추게 됩니다.
숫자로 따라가는 순전파 계산
영상의 중반부에서는 히든 차원을 2, 입력 차원을 3으로 두고, 가중치 행렬과 입력 시퀀스를 구체적인 숫자로 설정한 뒤 LSTM 한 타임스텝의 순전파를 끝까지 계산해 나갑니다.
1. x t x t 와 h t − 1 h t−1 를 concat하여 각 게이트의 선형 결합 W f x t , W i x t , W c x t , W o x t W f x t ,W i x t ,W c x t ,W o x t 를 구합니다.
2. 각 게이트에 sigmoid 또는 tanh를 적용해 f t , i t , C ~ t , o t f t ,i t , C ~ t ,o t 를 얻습니다.
3. 이전 셀 상태 C t − 1 C t−1 를 가정 값으로 두고,
C t = f t ⊙ C t − 1 + i t ⊙ C ~ t C t =f t ⊙C t−1 +i t ⊙ C ~ t
h t = o t ⊙ tanh ( C t ) h t =o t ⊙tanh(C t ) 를 실제 숫자를 대입해 계산합니다.
4. 마지막으로 fully-connected 층 가중치 W y W y 를 통해 로짓 g t = W y h t g t =W y h t 를 만들고, softmax를 적용해 최종 확률 벡터 y ^ t y ^ t 를 구함으로써 순전파를 마무리합니다.
이 파트 덕분에 추상적인 블록 다이어그램이 “행렬곱과 시그모이드·tanh·원소별 곱·덧셈의 조합”이라는 사실이 더 명확해지고, 코드 없이도 손으로 계산을 따라가 보며 LSTM 연산 흐름을 체감할 수 있습니다.
LSTM의 역전파(BPTT)와 5개 가중치의 기울기
후반부는 LSTM의 시간을 통한 역전파, 즉 BPTT를 다룹니다. 학습의 목표는 다섯 가중치 W f , W i , W c , W o , W y W f ,W i ,W c ,W o ,W y 각각에 대해 손실 L L에 대한 기울기를 구해, 경사하강법으로 업데이트하는 것이라고 정리합니다.
· 먼저 softmax–크로스 엔트로피 조합에서 얻는 ∂ L / ∂ g t = y ^ t − y t ∂L/∂g t = y ^ t −y t 를 이용해 ∂ L / ∂ W y ∂L/∂W y 를 체인 룰로 전개하고, 실제 숫자를 넣어 한 타임스텝 기준의 업데이트식을 도출합니다.
· 이어 output 게이트의 W o W o 에 대한 기울기 ∂ L / ∂ W o ∂L/∂W o 를 구하기 위해, ∂ L / ∂ h t ∂L/∂h t , ∂ h t / ∂ o t ∂h t /∂o t , ∂ o t / ∂ W o ∂o t /∂W o 를 차례대로 계산하는 과정을 자세히 보여 줍니다. 여기서 element-wise 곱의 미분을 선형대수 관점에서 풀어 설명해, 왜 ∂ h t / ∂ o t ∂h t /∂o t 에 tanh C t C t 만 남는지까지 짚어 줍니다.
· 그 다음은 forget·input·candidate 게이트의 가중치 W f , W i , W c W f ,W i ,W c 에 대한 기울기를 비슷한 패턴으로 전개합니다. 셀 상태 공식 C t = f t ⊙ C t − 1 + i t ⊙ C ~ t C t =f t ⊙C t−1 +i t ⊙ C ~ t 를 기준으로 ∂ L / ∂ C t ∂L/∂C t 를 먼저 구하고, 이를 다시 ∂ L / ∂ f t , ∂ L / ∂ i t , ∂ L / ∂ C ~ t ∂L/∂f t ,∂L/∂i t ,∂L/∂ C ~ t 로 나누어 가며 각 게이트에 대한 기울기 표현을 완성합니다.
영상에서는 시퀀스 길이를 1로 가정하고 수식을 전개하지만, 실제 다중 타임스텝에서는 RNN·LSTM에서처럼 각 시점의 기울기를 시간 방향으로 누적/전달한다는 점을 별도로 언급해, 코드 구현 시 확장 방향도 함께 안내합니다.
LSTM이 장기 의존성을 완화하는 메커니즘
마지막 파트에서는 “왜 LSTM은 RNN보다 장기 의존성 문제가 덜 심한가?”라는 질문을, 기울기의 전달 구조를 통해 설명합니다. RNN의 경우 시간 축을 따라 1보다 작은 값들이 계속 곱해져 기울기가 급격히 0으로 수렴하는 반면, LSTM에서는 셀 상태와 은닉 상태의 기울기가 단순 곱셈만이 아니라 덧셈 형태로도 전달되기 때문에 완전히 0으로 가라앉기 어렵다는 점을 강조합니다.
특히 forget 게이트의 sigmoid 출력 f t f t 가 0~1 사이, 보통 0.5 근처의 값을 갖기 때문에, 셀 상태 변화량에 대한 기울기가 완전히 사라지지 않고 일정 수준 이상 유지될 수 있는 “안전장치” 역할을 한다고 해석합니다. 물론 LSTM도 장기 의존성 문제가 100% 사라지는 것은 아니지만, 기본 RNN과 비교하면 긴 시퀀스를 훨씬 안정적으로 학습할 수 있는 이유를 수식 구조와 함께 보여 주는 부분이 인상적입니다.
영상의 끝에서 강의자는 LSTM이 1990년대 제안된 이후, 트랜스포머 같은 더 강력한 모델이 등장했지만 여전히 중요한 역사적·이론적 토대라는 점을 언급하며, 다음 영상에서의 LSTM 구현 강의로 자연스럽게 이어지는 학습 경로를 제안합니다. LSTM을 처음부터 끝까지 “왜 이렇게 설계됐는지” 이해하고 싶은 학습자라면, 이 강의를 본 뒤 개념·수식 흐름을 정리해 두고 RNN·트랜스포머로 이어가는 학습 루트에 활용하기에 적합한 콘텐츠입니다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 5강. LSTM, 초보자를 위한 안내서 | Deep Learning 101
딥러닝 101 - 5강. LSTM, 초보자를 위한 안내서 | Deep Learning 101
이 영상은 LSTM이 등장하게 된 배경부터 구조·순전파·역전파 알고리즘까지, “왜 이렇게 설계됐는지”를 직관과 수식으로 함께 풀어 주는 이론 중심 강의입니다. 특히 RNN의 장기 의존성 문제와
inner-game.tistory.com
6강. [Deep Learning 101] LSTM 파이썬으로 구현하기 (feat.훈민정음서문)
7강. [Deep Learning 101] Cross Entropy 크로스엔트로피 손실함수를 알아보자
이 영상은 크로스엔트로피 손실함수를 ‘정보·기대값·엔트로피’라는 세 가지 개념으로 풀어 가며, 분류 문제에서 왜 크로스엔트로피가 널리 쓰이는지 직관적으로 설명하는 강의이다. 단순 공식 설명을 넘어서 일상적인 비유와 예시를 통해, 수식을 처음 접하는 사람도 개념 흐름을 따라가기 좋게 구성되어 있다.
정보·놀람도와 기대값
· 영상은 크로스엔트로피 공식을 바로 보여준 뒤, 이를 이해하려면 먼저 ‘정보(놀람도)’ 개념을 알아야 한다고 하며, 낮은 확률의 사건이 발생할수록 더 많이 놀란다는 일상적 직관에서 출발한다.
· 동전·주사위 예제와 함께 “확률이 높을수록 덜 놀라고, 낮을수록 더 놀란다”는 점을 강조하고, 정보이론에서 놀람을 log ( 1 / p ( x ) ) log(1/p(x)), 즉 − log p ( x ) −logp(x)로 정의한다는 사실을 소개한다.
· 이어 축구팀 전력과 컨디션을 예로 들어, ‘값 × 확률’을 모두 더한 것이 기대값(예상 전력)이라는 점을 설명하며, 기대값이 “확률을 고려한 평균적 결과”라는 의미임을 자연스럽게 연결한다.
엔트로피와 예측 가능성
· 기대값의 틀을 이용해, “객관적인 전력 대신 놀람도(정보)를 넣으면 그것이 엔트로피”라는 식으로 엔트로피를 정의한다.
· 두 축구팀의 기량과 컨디션 분포가 다르지만 기대값은 같은 상황을 설정한 뒤, 어떤 팀이 더 예측 가능한지 비교하는 과정에서 엔트로피의 역할을 설명한다.
· 확률이 0.9나 0.1처럼 극단적일수록 플레이가 예측 가능하고 엔트로피는 낮으며, 0.5처럼 애매할수록 예측이 어렵고 엔트로피가 높아진다는 예시로 “엔트로피는 예측 불가능성의 척도”라는 직관을 잡을 수 있게 해 준다.
크로스엔트로피의 의미와 직관
· 여기까지의 내용을 바탕으로, 엔트로피 공식에서 확률 p ( x ) p(x) 대신 한쪽을 p ( x ) p(x), 다른 쪽을 q ( x ) q(x)로 바꾼 것이 크로스엔트로피임을 보여 준다.
· 실제 분포 p ( x ) p(x)는 ‘정답 레이블’, 모델이 예측한 분포 q ( x ) q(x)는 ‘신경망 출력 확률’로 두고, 두 분포가 다를수록 크로스엔트로피 값이 커져 “우리가 느끼는 불편함, 괴리”가 커지는 것으로 해석한다.
· 치킨 맛집 리뷰 예시를 통해, 리뷰 점수(사람들이 느낀 평균적 맛에 대한 확률 정보)와 실제로 먹어 본 맛이 크게 다를 때 느끼는 불편함이 곧 크로스엔트로피 손실의 직관적 의미와 유사하다고 비유한다.
신경망 학습에서의 활용
· 분류 문제에서 정답을 원-핫 벡터로 두면, 크로스엔트로피는 사실상 정답 클래스의 예측 확률에만 − log −log를 취하는 형태로 단순화되며, 정답 확률이 낮을수록 손실이 커진다는 점을 강조한다.
· 신경망은 이 손실을 최소화하는 방향으로 가중치를 업데이트하며, 사용되는 최적화 방법은 다른 딥러닝 모델과 마찬가지로 경사하강법과 역전파라는 점을 짚어 준다.
· 여러 샘플의 크로스엔트로피 값을 평균 내어 전체 배치 손실을 정의하고, 이를 반복적으로 줄여 나가며 모델이 실제 분포 p ( x ) p(x)에 가까운 q ( x ) q(x)를 예측하도록 학습된다는 설명으로 흐름을 마무리한다.
MSE와의 비교: 왜 크로스엔트로피인가
· 마지막으로, 분류 문제에서 평균제곱오차(MSE) 대신 크로스엔트로피를 더 선호하는 이유를 그래프와 함께 설명한다.
· 정답이 1인 이진 분류 상황에서, 예측값이 0에 가까울수록 크로스엔트로피는 MSE보다 훨씬 큰 손실과 기울기를 주어, “심하게 틀린” 예측에 더 강한 페널티를 부여한다는 점을 보여 준다.
· 이 덕분에 분류 문제에서는 크로스엔트로피가 MSE보다 손실과 그래디언트 측면에서 더 민감하게 반응하여, 잘못된 예측을 빠르게 수정하는 데 유리하다는 점을 강조하며 강의를 마무리한다.
전체적으로 이 영상은 교과서적인 정의와 정보이론의 맥락을 유지하면서도, 제비뽑기·축구·배달앱 같은 비유를 통해 직관을 쌓게 해 주는 구성이라, 크로스엔트로피 입문용 글을 쓰거나 개념 정리를 할 때 곁들여 참고하기 좋은 콘텐츠이다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 7강. Cross Entropy 크로스엔트로피 손실함수를 알아보자 | Deep Learning 101
딥러닝 101 - 7강. Cross Entropy 크로스엔트로피 손실함수를 알아보자 | Deep Learning 101
이 영상은 크로스엔트로피 손실함수를 ‘정보·기대값·엔트로피’라는 세 가지 개념으로 풀어 가며, 분류 문제에서 왜 크로스엔트로피가 널리 쓰이는지 직관적으로 설명하는 강의이다. 단순
inner-game.tistory.com
8강. [Deep Learning 101] 확률적 경사하강법을 소개합니다
이 영상은 경사하강법의 세 가지 변형인 배치 경사하강법, 확률적 경사하강법(SGD), 미니배치 경사하강법의 개념을 직관적인 비유와 간단한 수식, 파이썬 코드로 설명하는 입문 강의이다. 특히 “데이터를 어떤 순서·단위로 학습시키느냐”에 초점을 맞추어, 최적화 알고리즘의 큰 그림을 잡고 싶은 학습자에게 잘 맞는 구성이다.
로컬 미니마와 데이터 스케줄링
· 강의는 먼저 신경망 학습에서 손실 함수의 전역 최소값(글로벌 미니멈)이 아닌 지역 최소값(로컬 미니마)에 갇히는 문제가 존재한다는 점을 짚는다.
· 초기값 설정, 학습률 조정, 데이터 스케줄링 등 여러 대응 가운데, 이번 영상에서는 “학습 데이터의 사용 순서와 묶는 방식”을 바꾸는 전략이 곧 배치·SGD·미니배치 경사하강법의 차이임을 강조한다.
배치 경사하강법: 모든 데이터를 한 번에
· 간단한 선형 회귀 예제를 두고, 모든 데이터 포인트에 대해 오차를 계산한 뒤 평균을 내어 MSE 손실을 구하고, 그에 대한 기울기를 계산해 가중치 w w를 한 번 업데이트하는 과정을 보여준다.
· 이처럼 전체 데이터셋을 한 번에 사용해 기울기를 구하는 방식을 배치 경사하강법이라고 정의하며, 업데이트가 안정적이고 진동이 적다는 장점을 갖지만, 데이터가 많을수록 계산 비용이 매우 커진다는 단점을 지적한다.
확률적 경사하강법(SGD): 샘플 하나씩 업데이트
· 이어 동일한 예제에서, 매 업데이트마다 하나의 데이터 포인트만 랜덤으로 골라 손실과 기울기를 계산하고 바로 가중치를 업데이트하는 방식을 소개한다.
· 이 방식을 확률적 경사하강법이라고 부르며, 매번 적은 계산량으로 빠르게 업데이트할 수 있어 효율적이지만, 개별 샘플에 매우 민감해 손실 곡선이 요동치고 경로가 불안정해질 수 있다는 점을 설명한다.
· 다만 이러한 “노이즈 섞인 이동”이 오히려 로컬 미니마에 빠졌다가도 빠져나올 가능성을 어느 정도 높여 주는 효과가 있어, 완전히 나쁜 것만은 아니라는 해석도 덧붙인다.
미니배치 경사하강법: 안정성과 효율성의 절충
· 배치의 안정성과 SGD의 효율성을 동시에 어느 정도 누리는 방식으로, 미니배치 경사하강법을 제시한다.
· 이는 전체 데이터에서 임의로 일정 개수(예: 5개)의 샘플을 뽑아 그들에 대한 평균 손실과 평균 기울기를 계산해 가중치를 업데이트하는 방법이며, 배치보다 계산이 가볍고, SGD보다 기울기 추정이 안정적이라는 장점이 있다.
· 영상에서는 예제 데이터에서 두 개씩 묶어 기울기를 계산하고 업데이트하는 과정을 보여주며, 실제 딥러닝 학습에서 거의 항상 미니배치 방식이 사용된다는 실무적 맥락도 함께 언급한다.
파이썬 코드 예제와 정리
· 후반부에서는 동일한 회귀 데이터셋을 가지고 배치, SGD, 미니배치 각각에 대한 파이썬 코드 스니펫을 차례대로 소개한다.
· 배치 코드에서는 모든 x x와 ( y − y ^ ) (y− y ^ )를 한 번에 묶어 평균 기울기를 구하고, SGD 코드에서는 단 하나의 샘플을 선택해 기울기를 구한 뒤 업데이트하는 차이를 명확히 보여준다.
· 미니배치 코드에서는 전체 데이터에서 배치 크기만큼 인덱스를 샘플링해 그 하위 집합만 사용하여 기울기를 구하는 부분이 핵심이며, 나머지 업데이트 로직은 동일하다는 점을 강조한다.
이 영상은 수식, 숫자 예제, 코드가 함께 등장하지만 핵심 초점은 “데이터를 어떤 단위로, 어떤 순서로 사용할 것인가”라는 직관적 관점에 있어, 경사하강법의 변형들을 글 한 편으로 정리하기에 좋은 출발점이 되는 강의다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 8강. 확률적 경사하강법을 소개합니다 | Deep Learning 101
딥러닝 101 - 8강. 확률적 경사하강법을 소개합니다 | Deep Learning 101
이 영상은 경사하강법의 세 가지 변형인 배치 경사하강법, 확률적 경사하강법(SGD), 미니배치 경사하강법의 개념을 직관적인 비유와 간단한 수식, 파이썬 코드로 설명하는 입문 강의이다. 특히
inner-game.tistory.com
9강. [Deep Learning 101] 오토인코더 Autoencoder를 소개합니다
이 영상은 오토인코더의 개념·학습 방식·수식 수준의 학습 알고리즘·대표 활용까지를 짧고 간결하게 정리해 주는 입문 강의이다. 인코더–디코더 구조와 “입력과 거의 같은 출력을 내는데도 왜 쓸모가 있는지”를 잠재공간과 차원 축소 관점에서 설명해 주는 점이 특징이다.
오토인코더의 기본 아이디어
· 오토인코더는 입력 데이터를 더 작은 차원의 잠재공간(latent space, 코딩)으로 압축한 뒤, 다시 원본과 최대한 비슷하게 복원하도록 학습하는 신경망이다.
· 구조는 크게 인코더(압축)와 디코더(복원) 두 부분으로 나뉘며, 인코더가 “핵심 특징만 뽑아 요약본을 만드는 역할”, 디코더가 “요약본으로부터 원문을 재구성하는 역할”을 한다는 비유로 이해를 돕는다.
셀프지도·비지도 학습으로서의 오토인코더
· 개·고양이 분류처럼 입력–정답 라벨 쌍을 사용하는 지도 학습과 달리, 오토인코더는 “입력 = 정답”으로 두고 원본과 복원본의 차이(재구성 손실)를 최소화하는 방식으로 학습한다.
· 즉 별도의 라벨이 없는 데이터만으로도, 데이터 분포와 구조를 반영한 압축 표현을 배우는 비지도/셀프지도 학습 모델이라는 점을 강조한다.
잠재공간과 차원 축소의 의미
· 강의에서는 200페이지 책을 3페이지 요약본으로 줄이는 비유를 통해, 차원 축소가 불필요한 세부를 버리고 중요한 정보만 남기는 과정이라는 점을 직관적으로 설명한다.
· 입력보다 훨씬 작은 잠재공간으로 정보를 통과시키면, 네트워크는 “복원에 꼭 필요한 핵심 특징”만 통과시키도록 압박받게 되고, 이 과정에서 자연스럽게 데이터의 유용한 표현을 학습하게 된다고 설명한다.
순전파·역전파와 학습 알고리즘
· 예제에서는 작은 차원의 인코더–디코더 가중치 행렬을 설정하고, 단일 입력에 대해 순전파로
· · 1. 인코더 출력 z z 계산
· · 2. 디코더 출력 x ^ x ^ 계산
· · 3. 원본 x x와 출력 x ^ x ^ 의 차이를 MSE로 정의해 손실을 구하는 과정을 실제 숫자로 보여준다.
· 이어 체인 룰을 사용해 디코더 가중치, 인코더 가중치에 대한 손실의 기울기 ∂ L / ∂ W decoder , ∂ L / ∂ W encoder ∂L/∂W decoder ,∂L/∂W encoder 를 단계별로 전개하고, 시그모이드 미분까지 포함해 직접 값을 계산한다.
· 마지막에는 경사하강법 업데이트 W ← W − α ∇ W L W←W−α∇ W L를 적용해 가중치가 아주 조금씩 변하는 모습을 보여 주면서, 이런 과정을 반복하면 잠재공간이 점차 입력의 핵심 특성을 잘 표현하게 된다고 정리한다.
오토인코더의 대표 활용
· 영상 마지막 부분에서는 오토인코더의 특성을 “차원 축소 + 복원 능력”으로 요약하며, 이를 활용할 수 있는 대표 응용으로 차원 축소·특징 추출·노이즈 제거·복원·생성 등을 소개한다.
· 특히 스캔 문서나 디지털 이미지에서 노이즈를 제거하거나(Denoising Autoencoder), 흑백 이미지를 컬러로 복원하는 작업, 데이터의 압축·이상 탐지 등에 널리 응용된다는 점을 간략히 언급한다.
결국 이 강의는 “입력을 그대로 따라 그리게 만드는 모델이 어떻게 유용한지”를, 잠재공간과 재구성 손실, 수식 흐름, 그리고 실제 활용 예까지 연결해 한 번에 정리해 주는 오토인코더 입문용 콘텐츠라고 정리할 수 있다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 9강. 오토인코더 Autoencoder를 소개합니다 | Deep Learning 101
딥러닝 101 - 9강. 오토인코더 Autoencoder를 소개합니다 | Deep Learning 101
이 영상은 오토인코더의 개념·학습 방식·수식 수준의 학습 알고리즘·대표 활용까지를 짧고 간결하게 정리해 주는 입문 강의이다. 인코더–디코더 구조와 “입력과 거의 같은 출력을 내는데도
inner-game.tistory.com
10강. [Deep Learning 101] 오토인코더 PyTorch로 구현하기
11강. [Deep Learning 101] GAN 생성적 적대 신경망 Generative Adversarial Network
이 영상은 생성적 적대 신경망(GAN)의 아이디어와 구조, 그리고 제너레이터·디스크리미네이터가 이진 크로스엔트로피 손실을 두고 서로 경쟁하며 학습하는 과정을 직관적 비유와 간단한 수식 예제로 설명하는 입문 강의이다. 특히 “위조 화가 vs 감별사” 비유와 실제 숫자를 이용한 손실·기울기 계산으로, 적대적 학습의 흐름을 감각적으로 이해하기 좋다.
생성 모델로서의 GAN 개념
· 강의는 먼저 딥러닝 모델을 판별 모델(분류·회귀)과 생성 모델로 나누고, 인간이 “개념을 분류도 하지만 새로운 이미지를 그려 내기도 한다”는 점에서 생성 모델의 중요성을 짚는다.
· StyleGAN 얼굴 생성, 스타일 변환(말↔얼룩말, 모네↔사진), 초해상도(SRGAN)처럼 실제 애플리케이션 사례들을 보여 주며, GAN이 생성 모델 붐의 출발점이 된 역사적 의미를 간략히 소개한다.
제너레이터와 디스크리미네이터 구조
· GAN은 “위조 화가” 역할의 제너레이터(Generator)와 “감별사” 역할의 디스크리미네이터(Discriminator), 두 개의 신경망으로 이루어진다.
· 제너레이터는 랜덤 잠재 벡터 z z를 입력으로 받아, 실제 데이터(예: 사람 얼굴, RGB 벡터 등)와 구분하기 어려운 샘플을 생성하는 것이 목표다.
· 디스크리미네이터는 입력이 진짜(real)인지 가짜(fake)인지 구분하는 이진 분류기이며, 출력은 0~1 사이의 스칼라(“진짜일 확률”)로 시그모이드를 사용해 표현한다.
손실 함수와 학습 목표
· 디스크리미네이터는 진짜 샘플에 대해서는 1, 제너레이터가 만든 가짜 샘플에 대해서는 0을 출력하도록 학습되며, 이 때 이진 크로스엔트로피(Binary Cross Entropy) 손실을 사용한다.
· 영상에서 제시하는 손실은
· · 진짜 데이터에 대한 손실: − log D ( x ) −logD(x)
· · 가짜 데이터에 대한 손실: − log ( 1 − D ( G ( z ) ) ) −log(1−D(G(z)))
를 합한 형태로, 디스크리미네이터는 이 합을 최소화(또는 로그 항을 최대화)하도록 학습된다.
· 반대로 제너레이터는 G ( z ) G(z)가 디스크리미네이터에게 “진짜처럼” 보이도록, − log D ( G ( z ) ) −logD(G(z))를 최소화(혹은 log D ( G ( z ) ) logD(G(z))를 최대화)하는 방향으로 학습된다고 설명한다.
숫자로 따라가는 순전파·역전파 예제
· 강의에서는 입력·가중치 차원을 극단적으로 줄인 장난감 GAN을 설정해,
· · 제너레이터가 단순한 RGB 벡터를 출력하고
· · 진짜 빨간색 RGB를 타깃으로 학습하는 상황을 가정한다.
· 이때 진짜·가짜 각각에 대해 디스크리미네이터의 출력과 손실 값을 직접 계산하고, 이진 크로스엔트로피의 미분과 시그모이드의 도함수 σ ′ ( x ) = σ ( x ) ( 1 − σ ( x ) ) σ ′ (x)=σ(x)(1−σ(x))를 이용해 디스크리미네이터 가중치의 기울기를 체인 룰로 전개해 나간다.
· 이어 제너레이터 쪽에서는 손실이 디스크리미네이터 출력 D ( G ( z ) ) D(G(z))를 거쳐 G G의 가중치까지 어떻게 역전파되는지, 중간 항들을 하나씩 계산해 실제 수치로 보여 줌으로써 “제너레이터는 디스크리미네이터를 속이는 방향으로 업데이트된다”는 흐름을 명확히 드러낸다.
적대적 학습의 직관과 의의
· 위조 화가와 감별사가 서로의 실력을 끌어올리는 비유를 GAN 학습에 대응시키면서, 디스크리미네이터가 정교해질수록 제너레이터도 더 현실적인 샘플을 만들도록 압박받는, 상호 경쟁 구조를 강조한다.
· 이런 적대적 학습 덕분에 GAN은 명시적으로 확률밀도함수 p ( x ) p(x)를 모델링하지 않으면서도, 실제 데이터 분포와 매우 비슷한 샘플을 생성해 내는 강력한 생성 모델로 자리 잡았다는 점을 간단히 언급한다.
결국 이 영상은 “GAN이 무엇을, 왜, 어떻게 학습하는지”를 직관적 비유–구조도–이진 크로스엔트로피 수식–간단한 수치 예제까지 한 흐름으로 연결해 주는, 생성 모델 입문자용 GAN 개념 정리 강의라고 정리할 수 있다.
딥러닝 101 - 11강. GAN 생성적 적대 신경망 Generative Adversarial Network | Deep Learning 101
이 영상은 생성적 적대 신경망(GAN)의 아이디어와 구조, 그리고 제너레이터·디스크리미네이터가 이진 크로스엔트로피 손실을 두고 서로 경쟁하며 학습하는 과정을 직관적 비유와 간단한 수식
inner-game.tistory.com
12강. [Depp Learning 101] GAN (Generative Adversarial Network) 코드 구현
13강. [Deep Learning 101] Softmax와 Cross-Entropy의 미분
이 영상은 소프트맥스–크로스엔트로피 조합의 역전파에서 늘 등장하는 “기울기가 y ^ − y y ^ −y로 단순화된다”는 결과를 처음부터 끝까지 미분으로 직접 도출해 주는 이론 중심 강의이다. RNN·LSTM·다중 분류 신경망에서 반복해서 쓰이는 핵심 공식의 유도 과정을 한 번은 꼼꼼히 보고 싶을 때 참고하기 좋다.
소프트맥스의 편미분 정리
· 영상은 먼저 소프트맥스 출력을 y i = e o i ∑ k e o k y i = ∑ k e o k e o i 로 두고, 세 개의 출력 노드를 예로 들어 ∂ y i ∂ o j ∂o j ∂y i 를 구하는 것부터 시작한다.
· i = j i=j인 경우에는 ∂ y i ∂ o i = y i ( 1 − y i ) ∂o i ∂y i =y i (1−y i ), i ≠ j i =j인 경우에는 ∂ y i ∂ o j = − y i y j ∂o j ∂y i =−y i y j 로 정리되며, 이를 통해 소프트맥스의 야코비안 구조를 직관적으로 이해할 수 있게 한다.
크로스엔트로피와 체인 룰 결합
· 이어 다중 클래스 크로스엔트로피 손실 L = − ∑ k y k log y ^ k L=−∑ k y k log y ^ k 를 두고, ∂ L ∂ o j ∂o j ∂L 를 체인 룰로 전개한다.
· 먼저 ∂ L ∂ y ^ k = − y k y ^ k ∂ y ^ k ∂L =− y ^ k y k , 그리고 앞에서 구한 ∂ y ^ k ∂ o j ∂o j ∂ y ^ k 를 곱해 모두 더한 뒤, k = j k=j인 항과 k ≠ j k =j인 항을 나누어 정리한다.
원-핫 인코딩과 y ^ − y y ^ −y의 도출
· 원-핫 인코딩된 레이블을 가정하면, 한 클래스만 y j = 1 y j =1, 나머지는 0 0이므로 합 안의 많은 항들이 자연스럽게 사라진다.
· 정리 과정을 거치면 결국 ∂ L ∂ o j = y ^ j − y j ∂o j ∂L = y ^ j −y j 로 깔끔하게 수렴하며, 이것이 딥러닝 라이브러리들이 내부에서 사용하는 대표적인 그래디언트 형태임을 보여 준다.
실전에서 이 조합이 중요한 이유
· 소프트맥스–크로스엔트로피 조합은 RNN·LSTM·CNN·MLP 등 거의 모든 다중 분류 모델에서 출력층의 표준 조합으로 쓰이며, 기울기가 단순한 덕분에 역전파 구현이 쉬워지고 수치적으로도 안정적이다.
· 영상은 수식 전개 자체는 다소 길지만, 최종 결과가 “예측 확률 벡터에서 원-핫 레이블 벡터를 빼면 된다”로 끝나기 때문에, 이 조합이 현대 딥러닝에서 가장 널리 사랑받는 이유를 이해하는 데 큰 도움이 된다고 강조한다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 13강. Softmax와 Cross-Entropy의 미분 | Deep Learning 101
딥러닝 101 - 13강. Softmax와 Cross-Entropy의 미분 | Deep Learning 101
이 영상은 소프트맥스–크로스엔트로피 조합의 역전파에서 늘 등장하는 “기울기가 y ^ − y y ^ −y로 단순화된다”는 결과를 처음부터 끝까지 미분으로 직접 도출해 주는 이론 중심 강의이다. R
inner-game.tistory.com
14강. [Deep Learning 101] L1, L2 Regularization
이 영상은 L1, L2 정규화(regularization)가 왜 과적합을 줄이는지, 손실 함수에 어떤 형태로 들어가고 경사하강법에서 가중치가 어떻게 업데이트되는지까지 수식으로 보여주는 입문 강의다. 특히 “가중치에 페널티를 더해 학습을 일부러 방해하지만, 오히려 일반화 성능이 좋아진다”는 역설적인 아이디어를 직관과 미분 계산으로 함께 설명해 준다.
Regularization과 과적합 직관
· 강의는 먼저 모의고사 유형만 과도하게 외운 학생이 실제 시험에서 새로운 유형을 잘 못 푸는 비유로 과적합(overfitting)을 설명한다.
· 영화 추천 시스템 예시에서, 장르·감독처럼 중요한 특성과 개봉연도·상영시간처럼 덜 중요한 특성이 모두 모델에 들어가면 학습 데이터에는 잘 맞지만 새로운 데이터에서는 성능이 떨어질 수 있음을 보여 준다.
· 이런 상황에서 regularization은 “불필요한 가중치의 영향을 줄이거나 없애” 모델이 더 단순한 해를 택하도록 유도하는 방법이라고 정의한다.
L1 정규화: 절댓값 페널티와 희소성
· L1 정규화는 손실 함수에 λ ∑ i ∣ w i ∣ λ∑ i ∣w i ∣를 더하는 형태로, 모든 가중치의 절댓값 합을 페널티로 추가한다.
· 단순 1차 회귀 y = w x + b y=wx+b에 MSE 손실과 L1 항을 합친 뒤 ∂ L / ∂ w ∂L/∂w를 미분하면, 절댓값의 도함수 때문에 기울기에 부호(sgn)가 등장하고, 업데이트식이 “가중치의 부호 방향으로 일정량을 밀어 0에 더 가깝게 만드는” 꼴로 정리된다.
· 이 때문에 작은 가중치들은 반복 업데이트 과정에서 실제로 0까지 떨어지기 쉬워지고, 중요하지 않은 특성이 자동으로 제거된 희소(sparse) 모델이 되는 경향이 있다.
L2 정규화: 제곱 페널티와 weight decay
· L2 정규화는 손실 함수에 λ ∑ i w i 2 λ∑ i w i 2 를 더하며, 가중치 제곱 합을 페널티로 추가한다.
· 같은 설정에서 미분하면, ∂ L / ∂ w ∂L/∂w에 2 λ w 2λw 항이 추가되어, 업데이트식이 “기존 경사하강 업데이트 + 가중치를 비율로 줄이는 weight decay” 형태가 됨을 보여 준다.
· L1이 가중치의 크기와 상관없이 ‘일정량’을 깎는 데 비해, L2는 가중치가 클수록 더 큰 페널티를 주고, 작을수록 작은 페널티를 주기 때문에 전체 가중치를 부드럽게 줄이며 보다 안정적인 정규화 효과를 낸다고 설명한다.
L1 vs L2: 특징과 활용 차이
· L1: 절댓값 페널티로 인해 작은 가중치들을 0으로 만드는 경향이 강해, 특성 선택·차원 축소가 필요한 상황이나 희소한 표현을 선호할 때 유리하다.
· L2: 가중치의 제곱에 비례하는 페널티로, 특정 가중치만 0으로 만들기보다는 전체를 작게 유지해 모델 복잡도를 줄이고, 과적합을 완화하는 데 널리 사용된다.
· 강의는 마지막에 “카페의 적당한 소음이 오히려 공부에 도움될 때도 있다”는 비유를 들며, regularization이 학습을 방해하는 것처럼 보이지만 실제로는 더 일반화 잘 되는 모델을 만드는 ‘좋은 방해’가 될 수 있다고 정리한다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 14강. L1, L2 Regularization | Deep Learning 101
딥러닝 101 - 14강. L1, L2 Regularization | Deep Learning 101
이 영상은 L1, L2 정규화(regularization)가 왜 과적합을 줄이는지, 손실 함수에 어떤 형태로 들어가고 경사하강법에서 가중치가 어떻게 업데이트되는지까지 수식으로 보여주는 입문 강의다. 특히 “
inner-game.tistory.com
15강. [Deep Learning 101] Word2Vec 쉬운 예제로 개념잡기
이 영상은 Word2Vec의 기본 아이디어, CBOW·Skip-gram 구조, 그리고 “단어 의미를 벡터 공간에 어떻게 새기는지”를 작은 숫자 예제로 보여주는 입문 강의다. 원-핫 인코딩에서 시작해 임베딩과 학습 메커니즘까지 자연스럽게 이어져, NLP 초입을 다지기에 좋다.
원-핫 인코딩과 임베딩의 필요성
· 강의는 “I love 피자” 같은 예로 각 단어를 원-핫 벡터로 표현할 때,
· · 단어 간 의미 관계를 전혀 반영하지 못하고
· · 단어 수가 늘수록 차원이 폭증하는 문제가 있다고 짚는다.
· 이를 해결하는 기법이 단어 임베딩(word embedding) 이며, 단어를 더 낮은 차원의 실수 벡터로 매핑해
· · 의미가 비슷한 단어는 가까이, 다른 단어는 멀어지게 하고
· · 계산 효율성도 높이는 것을 목표로 한다고 설명한다.
Word2Vec 구조: 작은 신경망으로 임베딩 학습
· Word2Vec은 “단어 의미를 잘 보존하는 임베딩 벡터를 학습하는 매우 얇은 신경망”으로 소개된다.
· 예제에서는 단어 4개짜리 작은 어휘를 가정해
· · 입력층: 원-핫(차원 4)
· · 은닉층: 2차원 (임베딩 차원)
· · 출력층: 다시 4차원 구조를 두고, 실제 Word2Vec에서는 단어 수 수만, 임베딩 차원 300 정도로 확장된다고 덧붙인다.
· 은닉층에는 활성화 함수를 쓰지 않는 선형 층만 두는데, 이는
· · 방대한 데이터에서 계산 효율을 높이고
· · 단어들 간 관계를 비선형으로 “찌그러뜨리지 않고” 공평하게 표현하려는 의도일 수 있다고 해석한다.
CBOW(Continuous Bag of Words)의 학습 방식
· CBOW는 “주변 단어들(문맥, context)로 중앙 단어를 맞추는 빈칸 추론 문제”로 설명된다.
· 예를 들어 “I love 피자”에서 중앙 단어 love를 맞추기 위해, 양옆 단어 I, 피자를 입력으로 쓰는 식이다.
· 작은 예제에서는 I와 피자의 원-핫 벡터를 더해 평균을 내어(합이 1이 되도록) 은닉층으로 보낸 뒤,
· · 은닉층에서 선형변환을 거쳐 출력층 로짓을 만들고
· · softmax로 확률을 얻은 다음
· · 크로스엔트로피로 손실을 계산한다.
· 역전파와 경사하강법으로 두 가중치 행렬을 반복해서 업데이트하는데, 여기서는 수식만 간단히 제시하고 세부 계산은 생략한다.
학습이 만드는 의미 공간: 벡터 위치의 변화
· 은닉층 차원이 2라서, 각 단어의 은닉층 출력(=임베딩)을 2D 평면에 점으로 찍어 볼 수 있다고 설명한다.
· 초기에는 가중치가 랜덤이므로 “I, love, like, 피자” 같은 단어들이 아무렇게나 흩어져 있다.
· 그러나 CBOW/Skip-gram 학습을 반복하면,
· · 문맥이 비슷한 love, like는 같은 문장 패턴에서 자주 중앙 단어로 등장해 비슷한 업데이트를 받으므로 점점 가까워지고
· · 문맥 역할이 다른 I, 피자는 다른 위치로 멀어지는 경향을 보이게 된다.
· 이 과정을 수십·수백만 문장에 대해 수행하면 “동일 문맥에 자주 등장하는 단어일수록 벡터 공간에서도 가까워진다”는 Word2Vec의 핵심이 자연스럽게 성립한다.
Skip-gram: 중심 단어로 주변 단어 예측
· 영상 후반부에서는 Word2Vec의 두 학습 방식, CBOW와 Skip-gram을 짝으로 정리한다.
· Skip-gram은 CBOW의 반대로,
· · 중앙 단어를 입력으로 주고
· · 그 주변(윈도우 내)의 단어들을 맞추도록 학습하는 구조다.
· “I love 피자”에서 window=1이라면
· · love의 주변: I, 피자
· · I의 주변: love
· · 피자의 주변: love
식으로 (중앙, 주변) 쌍들을 많이 만들고, 중앙 단어 임베딩이 그 주변 단어들을 잘 예측하도록 학습한다.
· CBOW/Skip-gram 모두, 결국 같은 문장에서 자주 함께 등장하는 단어쌍으로부터 임베딩을 업데이트하기 때문에, 의미적으로 유사한 단어는 결국 벡터 공간에서 서로 가까이 위치하게 된다.
이 강의는 원-핫 인코딩의 한계에서 출발해, Word2Vec이 어떻게 저차원 임베딩 공간 안에 단어 의미와 문맥을 녹여 넣는지, 그리고 CBOW·Skip-gram의 학습 과정을 직관 위주로 이해하는 데 특히 도움이 되는 콘텐츠다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 15강. Word2Vec 쉬운 예제로 개념잡기 | Deep Learning 101
딥러닝 101 - 15강. Word2Vec 쉬운 예제로 개념잡기 | Deep Learning 101
이 영상은 Word2Vec의 기본 아이디어, CBOW·Skip-gram 구조, 그리고 “단어 의미를 벡터 공간에 어떻게 새기는지”를 작은 숫자 예제로 보여주는 입문 강의다. 원-핫 인코딩에서 시작해 임베딩과 학습
inner-game.tistory.com
16강. [Deep Learning 101] KL Divergence
이 영상은 KL Divergence를 “크로스엔트로피에서 엔트로피를 뺀 값”이라는 정보이론 관점과, 치킨집·맛집 비유를 활용한 직관적 설명으로 풀어내는 짧은 입문 강의다. VAEs 등 생성 모델에서 KL 항이 왜 등장하는지 이해할 때 기초가 되는 내용에 초점을 맞추고 있다.
KL Divergence의 정의와 직관
· KL Divergence는 두 확률분포 P P와 Q Q 사이의 정보량 차이를 재는 척도로, 공식은 D K L ( P ∥ Q ) = ∑ x P ( x ) log P ( x ) Q ( x ) D KL (P∥Q)=∑ x P(x)log Q(x) P(x) 꼴로 정의된다.
· 식을 전개하면 D K L ( P ∥ Q ) = H ( P , Q ) − H ( P ) D KL (P∥Q)=H(P,Q)−H(P), 즉 “크로스엔트로피(타 분포로 측정했을 때의 평균 놀람)에서 원래 분포의 엔트로피(자체 불확실성)를 뺀 값”이 되어, 기준 분포 자체의 난이도를 제거한 순수한 분포 차이로 해석할 수 있다.
맛집 비유로 보는 의미
· 강의에서는 치킨집 리뷰 예시를 활용해, P ( x ) P(x)를 많은 사람의 평가가 만든 실제 맛 분포, Q ( x ) Q(x)를 본인의 체감 맛 분포로 비유한다.
· 크로스엔트로피가 “맛집 리뷰를 믿고 갔다가 크게 실망했을 때의 평균 놀람”이라면, KL Divergence는 여기서 해당 음식(예: 엄마손맛 치킨)이 원래 가진 조리·맛의 불확실성(엔트로피)을 뺀 값이어서, **가게의 솜씨/평가와 실제 경험 사이의 ‘순수한 괴리’**를 측정한다고 설명한다.
계산 예제와 값의 해석
· 영상에서는 단순한 이산 분포 두 개를 가정해 KL Divergence를 직접 계산해 보며, 두 분포가 더 비슷해질수록 값이 0에 가까워짐을 확인해 준다.
· 반대로 분포가 많이 다르면 KL 값이 커지며, 값의 범위가 0 0에서 ∞ ∞까지 뻗어 있다는 점, 두 분포가 같으면 0이 된다는 성질을 짚어 준다.
비대칭성과 Jensen-Shannon Divergence
· KL Divergence는 일반적인 ‘거리’가 아니라 비대칭 척도라서, D K L ( P ∥ Q ) D KL (P∥Q)와 D K L ( Q ∥ P ) D KL (Q∥P)가 서로 다르며, 어느 쪽을 기준 분포로 둘지에 따라 값과 의미가 달라진다는 점을 강조한다.
· 이 비대칭성과 값의 스케일(0~무한대) 때문에, 두 분포 차이를 보다 대칭적이고 부드럽게 보고 싶을 때는 Jensen–Shannon Divergence(JSD)를 사용한다고 소개한다.
· JSD는 두 분포의 중간 분포 M = 1 2 ( P + Q ) M= 2 1 (P+Q)를 둔 뒤, 1 2 ( D K L ( P ∥ M ) + D K L ( Q ∥ M ) ) 2 1 (D KL (P∥M)+D KL (Q∥M))으로 정의하며, 0~1 사이로 정규화되고 대칭인 점 때문에 GAN 등에서 자주 활용된다고 덧붙인다.
이 영상을 통해 KL Divergence가 “엔트로피·크로스엔트로피와 연결된, 두 분포 간 평균 정보량 차이”라는 점과, 비대칭성과 JSD로의 확장이 어떤 의미를 갖는지 직관적으로 정리할 수 있다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 16강. KL Divergence | Deep Learning 101
딥러닝 101 - 16강. KL Divergence | Deep Learning 101
이 영상은 KL Divergence를 “크로스엔트로피에서 엔트로피를 뺀 값”이라는 정보이론 관점과, 치킨집·맛집 비유를 활용한 직관적 설명으로 풀어내는 짧은 입문 강의다. VAEs 등 생성 모델에서 KL 항
inner-game.tistory.com
17강. [Deep Learning 101] 시퀀스-투-시퀀스, Seq2seq 모델을 소개합니다
이 영상은 시퀀스-투-시퀀스(seq2seq) 모델의 구조와 작동 원리를 LSTM·Word2Vec과 연결해 설명하면서, 기계번역을 중심으로 인코더–컨텍스트 벡터–디코더 흐름을 잡아 주는 입문 강의이다. 특히 “길이가 다른 입력·출력 시퀀스를 어떻게 다루는가”를 직관적으로 이해하는 데 초점을 두고 있다.
Seq2seq가 필요한 이유
· 영상은 먼저 기계번역에서 단어 수, 어순이 언어마다 일대일로 대응하지 않는다는 점을 지적하며, 단순 RNN/LSTM만으로는 이 문제를 풀기 어렵다는 맥락을 제시한다.
· LSTM이 장기 의존성 문제를 완화해 주긴 하지만, “문장 전체를 하나의 의미 벡터로 압축하고 다시 새로운 문장으로 풀어내는 구조”가 필요해 등장한 것이 seq2seq 모델이라고 설명한다.
인코더: 입력 문장을 컨텍스트 벡터로
· 예시 문장 “thank you”를 영어→한국어 번역하는 상황을 두고, 우선 각 단어를 Word2Vec 임베딩으로 변환한 뒤 LSTM 인코더에 순차적으로 넣는 과정을 그려 보인다.
· LSTM은 각 시점마다 셀 상태 C t C t 와 히든 상태 h t h t 를 업데이트하며, 마지막 단어(EOS 포함)를 처리한 뒤 얻어지는 ( C T , h T ) (C T ,h T )가 입력 전체를 요약한 벡터가 된다.
· seq2seq에서는 이 ( C T , h T ) (C T ,h T )를 합쳐 컨텍스트 벡터(context vector) 라 부르고, 인코더의 출력이자 디코더의 입력으로 사용한다.
디코더: 컨텍스트에서 출력 시퀀스 생성
· 디코더 역시 별도의 LSTM으로 구성되며, 인코더와 가중치를 공유하지 않고 독립된 파라미터를 가진다.
· 디코더의 첫 시점에서는 인코더가 만든 컨텍스트 벡터를 초기 상태로 주고, 동시에 문장 시작 토큰(EOS/SOS)을 입력하여 첫 한국어 단어(예: “고마워”)를 예측한다.
· 이때 디코더의 히든 상태는 다시 Word2Vec(한국어 임베딩)과 출력층, softmax를 거쳐 다음 단어의 확률 분포를 생성하고, 선택된 단어를 다음 시점의 입력으로 반복적으로 사용하여 “고마워요”, “고마워요 EOS”처럼 문장을 완성한다.
학습과 역전파의 흐름
· 학습 시에는 디코더에서 예측한 각 단어의 분포와 실제 정답 문장을 원-핫 벡터로 비교하여, 크로스엔트로피 손실을 시퀀스 길이만큼 누적한다.
· 역전파는 디코더의 마지막 시점부터 시작해 softmax–크로스엔트로피 층을 거쳐 LSTM 가중치까지 전달되고, 이후 BPTT를 통해 컨텍스트 벡터를 경유하여 인코더 쪽 LSTM의 가중치까지 거슬러 올라간다.
· 이렇게 인코더·디코더 두 LSTM이 함께 업데이트되면서, 인코더는 “잘 압축된 의미 벡터”를, 디코더는 “그 벡터에서 자연스러운 번역을 펼치는 규칙”을 점점 더 잘 학습하게 된다.
Seq2seq의 의의와 확장
· 영상은 seq2seq가 인코더–컨텍스트–디코더 구조 덕분에 “입·출력 길이가 달라도 되는” 번역·요약·챗봇 등 다양한 시퀀스 변환 문제에 적용된다는 점을 강조한다.
· 이어 이 구조 위에 어텐션 메커니즘이 추가되면 긴 문장에서도 더 안정적인 성능을 내게 되고, 더 나아가 트랜스포머로 발전했다는 계보를 언급하며, 딥러닝·NLP 공부에서 반드시 짚고 넘어가야 할 기본 모델로 정리한다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 17강. 시퀀스-투-시퀀스, Seq2seq 모델을 소개합니다 | Deep Learning 101
딥러닝 101 - 17강. 시퀀스-투-시퀀스, Seq2seq 모델을 소개합니다 | Deep Learning 101
이 영상은 시퀀스-투-시퀀스(seq2seq) 모델의 구조와 작동 원리를 LSTM·Word2Vec과 연결해 설명하면서, 기계번역을 중심으로 인코더–컨텍스트 벡터–디코더 흐름을 잡아 주는 입문 강의이다. 특히
inner-game.tistory.com
18강. [Deep Learning 101] 시퀀스-투-시퀀스 나만의 챗봇 모델을 만들어보자
19강. [Deep Learning 101] Seq2seq+Attention 모델을 소개합니다
이 영상은 기존 seq2seq에 어텐션 메커니즘을 더해, 긴 입력 문장에서 디코더가 “어떤 단어를 얼마나 참고해야 하는지”를 동적으로 계산하는 과정을 직관적으로 보여 주는 강의다. 인코더–컨텍스트–디코더 구조 위에 dot-product 기반 어텐션을 얹는 기본 형태를 이해하기에 적합하다.
Seq2seq 한계와 어텐션의 필요성
· 기본 seq2seq는 인코더가 입력 전체를 고정 길이 컨텍스트 벡터 하나로 압축하기 때문에, 입력 시퀀스가 길어질수록 모든 정보를 이 한 벡터에 담기 어렵다는 문제가 있다.
· 어텐션은 디코더가 출력 각 시점마다 “인코더의 어떤 시점(hidden state)에 더 집중할지”를 학습해, 긴 문장이나 복잡한 구조에서도 번역 품질과 장기 의존성 처리를 개선한다.
인코더 출력 보존과 어텐션 스코어 계산
· 어텐션을 쓰는 seq2seq에서는 인코더의 마지막 상태만 쓰지 않고, 각 시점의 은닉 상태 h 1 e n c , h 2 e n c , … h 1 enc ,h 2 enc ,…를 모두 저장해 둔다.
· 디코더에서 어떤 시점 t t의 은닉 상태 h t d e c h t dec 가 있을 때, 이 벡터를 기준으로 인코더의 각 은닉 상태와의 유사도를 attention score로 계산한다.
· 영상에서는 가장 단순한 dot-product 방식을 사용해, 예를 들어 인코더 상태 ( 0.8 , 0.2 ) (0.8,0.2), 디코더 상태 ( 0.7 , 0.3 ) (0.7,0.3)이면 내적 0.8 ⋅ 0.7 + 0.2 ⋅ 0.3 = 0.62 0.8⋅0.7+0.2⋅0.3=0.62와 같은 식으로 점수를 구한다.
소프트맥스 정규화와 가중합 컨텍스트 벡터
· 이렇게 얻은 attention score들을 softmax에 통과시켜 확률 분포(어텐션 가중치)로 만든다.
· 각 인코더 은닉 상태에 이 가중치를 곱해 “중요한 입력일수록 값이 증폭되도록” 만들고, 이 가중치가 적용된 은닉 상태들을 모두 더해 새로운 컨텍스트 벡터를 구성한다.
· 이 컨텍스트 벡터는 기존 seq2seq의 고정 컨텍스트 벡터보다 훨씬 “현재 디코더 시점에 맞춰진 요약정보”이므로, 디코더의 다음 LSTM 입력이나 출력층에 함께 사용되어 더 정확한 예측을 돕는다.
디코더에서의 반복 적용과 효과
· 디코더는 각 시점마다 자신의 은닉 상태를 기준으로 새로운 attention score를 계산하고, 그에 따라 매번 다른 컨텍스트 벡터를 만들어 사용한다.
· 출력 토큰이 EOS가 나올 때까지 이 과정을 반복하며, 매번 “현재 생성하려는 단어와 가장 관련이 높은 입력 위치”에 더 많은 주의를 기울이게 된다.
· 이 메커니즘 덕분에 모델은 단순 seq2seq보다 긴 문장에 강하고, 어느 입력 단어를 참조해 어떤 출력 단어를 만들었는지 attention 분포를 통해 해석 가능하다는 장점도 얻는다.
영상은 수식을 최소화하고, dot-product·softmax·가중합이라는 세 단계만으로 “어텐션이 seq2seq에 어떻게 붙고, 무엇이 달라지는지”를 감각적으로 파악하게 해 주는 입문용 설명이라고 볼 수 있다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 19강. Seq2seq+Attention 모델을 소개합니다 | Deep Learning 101
딥러닝 101 - 19강. Seq2seq+Attention 모델을 소개합니다 | Deep Learning 101
이 영상은 기존 seq2seq에 어텐션 메커니즘을 더해, 긴 입력 문장에서 디코더가 “어떤 단어를 얼마나 참고해야 하는지”를 동적으로 계산하는 과정을 직관적으로 보여 주는 강의다. 인코더–컨
inner-game.tistory.com
20강. [Deep Learning 101] Seq2seq+Attention 코드로 챗봇을 업그레이드 합시다.
21강. [Deep Learning 101] 트랜스포머, 스텝 바이 스텝
이 영상은 트랜스포머의 인코더–디코더 구조, 위치 인코딩, 멀티헤드 셀프 어텐션, 잔차 연결·정규화, 피드포워드 네트워크, 마스크드 디코더까지를 작은 장난감 예제로 “끝까지 손으로 따라갈 수 있게” 보여주는 스텝바이스텝 강의입니다. 특히 Q·K·V 계산과 어텐션 행렬, 마스크드 어텐션의 동작이 수치 수준에서 펼쳐지는 것이 장점입니다.
전체 구조와 임베딩·위치 인코딩
· 트랜스포머는 크게 인코더 스택과 디코더 스택으로 구성되며, 각 블록 안에는 멀티헤드 어텐션, Add & Norm, 피드포워드, 다시 Add & Norm이 반복되는 모듈형 구조를 갖습니다.
· 입력 문장은 먼저 단어 인덱스로 토크나이즈되고, 단어 임베딩 레이어를 거쳐 고정 길이 벡터(영상에선 6차원)로 변환됩니다.
· 여기에 사인·코사인 기반 위치 인코딩(positional encoding) 을 더해, 동일한 단어라도 위치에 따라 다른 벡터가 되도록 만들어 어순 정보를 반영합니다.
인코더: 멀티헤드 셀프 어텐션과 피드포워드
· 인코더 블록에서는 “입력 + 위치 인코딩”을 복사해 Q, K, V 세 행렬을 만들고, 각각 다른 가중치 행렬과 곱해 선형 변환된 Q , K , V Q,K,V를 얻습니다.
· 셀프 어텐션은 Q K ⊤ QK ⊤ 을 계산해 토큰 간 유사도 스코어를 만들고, 차원 수의 제곱근으로 나누어(scale) softmax를 취함으로써 각 토큰이 다른 토큰에 얼마나 주의를 줄지 나타내는 확률 행렬을 만듭니다.
· 이 어텐션 행렬에 V V를 곱해 “입력 문맥을 반영한 새로운 표현”을 얻고, 여러 헤드에서 얻은 결과를 concat 후 선형층을 통과시키면 멀티헤드 어텐션의 출력이 됩니다.
· 이후 원래 입력(임베딩+포지션)을 더하는 잔차 연결(skip connection) 과 레이어 정규화(Add & Norm)를 거쳐, 두 층짜리 ReLU 피드포워드 네트워크를 통과시킨 뒤 다시 잔차+정규화를 적용하면 인코더 출력이 완성됩니다.
디코더: 마스크드 셀프 어텐션과 인코더–디코더 어텐션
· 디코더 입력도 마찬가지로 단어 임베딩+위치 인코딩으로 시작합니다.
· 첫 번째 멀티헤드 어텐션은 마스크드 셀프 어텐션 으로, Q K ⊤ QK ⊤ 행렬의 미래 위치(아직 생성되지 않은 토큰 위치)에 − ∞ −∞를 더해 softmax 후 해당 위치의 가중치가 0이 되게 하여, 디코더가 미래 단어를 미리 보지 않도록 합니다.
· 두 번째 멀티헤드 어텐션은 인코더–디코더 어텐션으로, 디코더의 은닉 상태에서 나온 Q Q와 인코더 출력에서 온 K , V K,V를 사용해 “출력 각 시점이 입력 문장의 어떤 위치에 주목할지”를 학습합니다.
· 이 뒤에도 인코더와 같은 구조의 피드포워드·잔차·정규화를 거치며, 최종적으로 선형층을 통해 단어장 크기(예: 11)로 차원을 펼친 뒤 softmax로 다음 토큰 확률을 출력합니다.
마스크와 자기어텐션의 의미
· 인코더의 셀프 어텐션은 “하나의 시퀀스 안에서 단어들끼리 서로 얼마나 관련 있는지”를 병렬적으로 계산하기 때문에, 긴 문장에서도 모든 단어쌍 의존성을 한 번에 포착할 수 있습니다.
· 디코더의 마스크드 셀프 어텐션은 오토레그레시브(autoregressive) 생성 조건을 만족시키기 위해, 현재까지 생성된 단어들만 보고 다음 단어를 예측하도록 제한합니다.
· 이런 설계 덕분에 트랜스포머는 RNN 계열과 달리 시퀀스를 순차적으로 처리하지 않고 완전히 병렬화된 어텐션 연산으로 긴 문맥을 다루면서도 높은 효율을 유지하는 모델이 되었고, 이후 다양한 대형 언어모델과 멀티모달 모델의 기반이 되었다고 영상은 강조합니다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 21강. 트랜스포머, 스텝 바이 스텝 | Deep Learning 101
딥러닝 101 - 21강. 트랜스포머, 스텝 바이 스텝 | Deep Learning 101
이 영상은 트랜스포머의 인코더–디코더 구조, 위치 인코딩, 멀티헤드 셀프 어텐션, 잔차 연결·정규화, 피드포워드 네트워크, 마스크드 디코더까지를 작은 장난감 예제로 “끝까지 손으로 따라
inner-game.tistory.com
22강. [Deep Learning 101] 트랜스포머로 (또) 챗봇만들기
23강. [Deep Learning 101] Variational Autoencoder, 변분오토인코더 VAEs를 알아보자
이 영상은 오토인코더에서 한 단계 더 나아가, 잠재공간을 확률분포(정규분포) 로 모델링해 새로운 데이터를 생성할 수 있게 해 주는 변분 오토인코더(VAE)의 구조와 동작을 직관적 비유와 수치 예제로 설명한다. 특히 평균·분산, 재파라미터라이제이션 트릭, 재구성 손실+KL 발산으로 이루어진 손실까지 한 번에 개념을 잡을 수 있다.
오토인코더 vs VAE: 잠재공간의 차이
· 일반 오토인코더는 입력을 잠재 벡터 z z 하나로 압축했다가 다시 복원하며, 이 z z는 “블랙박스” 같은 고정 벡터라서 사용자가 의미 있게 조절하거나 새로운 샘플을 만들기는 어렵다.
· VAE는 잠재공간을 “평균 μ μ와 분산 σ 2 σ 2 ”로 표현되는 정규분포로 모델링해, 각 데이터가 잠재공간의 분포로 매핑되도록 강제하고, 이 분포에서 샘플링한 z z로 새로운 데이터를 생성할 수 있도록 설계된다.
치킨 소스 비유로 보는 잠재공간
· 영상은 치킨 프랜차이즈 비유를 사용한다. 오토인코더의 잠재공간은 “본사가 준 비법 소스”처럼 레시피를 알 수 없고 그대로 재현만 가능한 상태로, 사람이 조절해 새로운 맛을 만들기 어렵다.
· VAE의 잠재공간은 “특제 소스의 재료 비율(평균·분산)을 공개한 상태”에 비유되어, 레시피를 이해하고 비율을 조절해 새로운 양념치킨(새 샘플)을 만들어 볼 수 있는 구조라고 설명한다.
인코더: μ μ, log σ 2 logσ 2 와 재파라미터라이제이션 트릭
· 인코더는 입력 벡터를 받아 은닉층을 거친 뒤, 두 개의 선형층을 통해 잠재공간의 평균 μ μ와 로그 분산 log σ 2 logσ 2 를 출력한다.
· 여기서 분산 대신 log σ 2 logσ 2 를 쓰는 이유는 분산을 항상 양수로 유지하기 쉽고, 수치 안정성이 좋기 때문이다.
· 샘플링 단계에서는 재파라미터라이제이션 트릭을 사용해
σ = exp ( log σ 2 ) , z = μ + σ ⊙ ϵ , ϵ ∼ N ( 0 , I ) σ= exp(logσ 2 ) ,z=μ+σ⊙ϵ,ϵ∼N(0,I)
꼴로 z z를 만든다. 이 방식 덕분에 샘플링 연산을 통해서도 μ , σ μ,σ에 대한 그래디언트를 역전파할 수 있다.
디코더와 손실: 재구성 + KL 발산
· 디코더는 샘플링된 z z를 입력으로 받아, 일반 오토인코더처럼 복원 벡터 x ^ x ^ 를 출력한다.
· 손실은 두 부분으로 구성된다.
· · 재구성 손실: 원본 x x와 복원 x ^ x ^ 사이의 차이(MSE나 BCE 등)를 측정해, 데이터 정보를 잘 보존하도록 유도한다.
· · KL Divergence: 인코더가 만든 잠재분포 q ( z ∣ x ) = N ( μ , σ 2 ) q(z∣x)=N(μ,σ 2 )가 표준 정규분포 N ( 0 , I ) N(0,I)에 가까워지도록,
D K L ( q ( z ∣ x ) ∥ N ( 0 , I ) ) = 1 2 ∑ i ( μ i 2 + σ i 2 − log σ i 2 − 1 ) D KL (q(z∣x)∥N(0,I))= 2 1 i ∑ (μ i 2 +σ i 2 −logσ i 2 −1)
형태의 항을 더한다.
· 최종 손실은 “재구성 손실 + KL 발산”으로, 인코더·디코더 전체에 역전파를 통해 가중치를 업데이트한다. 이렇게 학습하면 잠재공간이 자연스럽게 표준 정규분포 근처에서 잘 구조화된 형태로 정리된다.
VAE의 의의와 활용 방향
· VAE는 “데이터를 잘 복원하면서도 잠재공간이 정규분포를 따르도록” 학습하기 때문에, 학습 후에는 그저 N ( 0 , I ) N(0,I)에서 z z를 샘플링해 디코더에 넣는 것만으로도 학습 데이터와 유사한 새로운 샘플을 쉽게 생성할 수 있다.
· 영상에서는 이러한 잠재공간 제어 아이디어가 이후 언어 모델·이미지 생성 모델과 결합되어, 스테이블 디퓨전과 같은 현대적 생성 모델의 기반이 되었다는 점을 짚으며, VAE를 “잠재공간을 사람 손에 쥐여 준 첫 주요 생성 모델”로서의 의의를 강조한다.
딥러닝 101 - 23강. Variational Autoencoder, 변분오토인코더 VAEs를 알아보자 | Deep Learning 101
이 영상은 오토인코더에서 한 단계 더 나아가, 잠재공간을 확률분포(정규분포) 로 모델링해 새로운 데이터를 생성할 수 있게 해 주는 변분 오토인코더(VAE)의 구조와 동작을 직관적 비유와 수치
inner-game.tistory.com
24강. [Deep Learning 101] VAE를 만들어보자
25강. [Deep Learning 101] ResNet 잔차신경망이란? (feat.기울기소실문제)
이 영상은 기울기 소실(vanishing gradient) 문제를 간단한 3층 신경망 손계산으로 직접 보여 준 뒤, 같은 구조에 스킵 커넥션을 추가했을 때 기울기가 어떻게 달라지는지 비교하며 ResNet의 핵심 아이디어를 설명하는 강의입니다. “ResNet이 좋다더라” 수준의 직관을, 실제 숫자로 확인해 보는 데 초점이 맞춰져 있습니다.
깊은 신경망과 기울기 소실 문제
· 영상은 먼저 시그모이드/하이퍼볼릭 탄젠트 활성함수를 사용하는 심층 신경망에서, 층이 깊어질수록 역전파 과정에서 기울기가 체인 룰에 의해 계속 곱해지며 0에 가까워지는 현상이 발생함을 설명합니다.
· 실제로 3층짜리 단순 신경망을 가정하고 모든 가중치를 0.1, 활성함수를 시그모이드로 둔 뒤, 출력층에서 입력층 방향으로 ∂ L / ∂ w 3 , ∂ L / ∂ w 2 , ∂ L / ∂ w 1 ∂L/∂w 3 ,∂L/∂w 2 ,∂L/∂w 1 을 계산하면, 초기층으로 갈수록 기울기가 급격히 작아지는 것을 수치로 보여 줍니다.
스킵 커넥션 없는 경우: 급격히 줄어드는 기울기
· 시나리오 1(일반 신경망)에서는 입력 0.5, 모든 가중치 0.1로 설정하고 순전파를 통해 각 은닉층과 출력값을 구한 뒤, MSE 손실을 기준으로 역전파를 수행합니다.
· 이때 출력층 가중치 w 3 w 3 의 기울기는 비교적 크지만, ∂ L / ∂ w 2 ∂L/∂w 2 , ∂ L / ∂ w 1 ∂L/∂w 1 로 갈수록 값이 0에 근접해 가며, “입력에 가까운 가중치일수록 거의 업데이트되지 않는” 전형적인 기울기 소실 패턴이 나타난다는 점을 계산 과정으로 확인합니다.
스킵 커넥션 추가: 잔차 신경망 구조
· 시나리오 2에서는 동일한 구조에 스킵 커넥션(skip connection) 을 하나 추가해, 은닉층을 통과한 출력에 입력을 그대로 더한 형태(잔차 연결)를 갖도록 수정합니다.
· 순전파에서는 출력이 두 경로(기존 경로 + 스킵 경로)를 통해 결정되며, 손실은 여전히 MSE로 계산됩니다.
· 역전파에서는 출력이 입력까지 직접 연결되는 경로가 생기면서, ∂ L / ∂ w 1 ∂L/∂w 1 에 도달하는 기울기가 “기존 경로만 있을 때보다 덜 희미해지는” 결과가 나타나고, 실제 수치로 비교했을 때 초기층 기울기가 일반 신경망 대비 확연히 크다는 점을 보여 줍니다.
ResNet의 아이디어: 잔차 학습과 안정된 기울기 흐름
· 영상은 이러한 스킵 커넥션을 통해 각 블록이 H ( x ) H(x) 를 직접 학습하는 대신 F ( x ) = H ( x ) − x F(x)=H(x)−x, 즉 입력 대비 잔차(residual)를 학습하도록 바꾼 것이 ResNet의 핵심이라고 설명합니다.
· 이 방식은
· · 입력 x x를 그대로 다음 층으로 전달하는 대체 경로(gradient shortcut) 를 만들어, 기울기가 여러 비선형 층을 거치지 않고도 초깊은 층까지 도달할 수 있게 하고
· · 결과적으로 네트워크 깊이가 20층→50층→100층 이상으로 깊어져도 학습 성능이 떨어지지 않고 오히려 향상되는 기반을 마련했다고 정리합니다.
정리: 간단한 더하기가 만든 차이
· 영상의 마지막에서는 “가중치가 없는 단순한 더하기 연결” 하나가, 깊은 네트워크에서 기울기 소실 문제를 획기적으로 완화하고 최적화 경로를 부드럽게 만들어 준다는 점을 강조합니다.
· ResNet이 이후 대부분의 비전 모델과 다양한 변형 아키텍처(ResNeXt, DenseNet 등)에 큰 영향을 끼친 만큼, 이 손계산 예제는 스킵 커넥션의 역할을 감으로 이해하는 데 좋은 출발점이 된다고 결론짓습니다.
[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 25강. ResNet 잔차신경망이란? (feat.기울기소실문제) | Deep Learning 101
딥러닝 101 - 25강. ResNet 잔차신경망이란? (feat.기울기소실문제) | Deep Learning 101
이 영상은 기울기 소실(vanishing gradient) 문제를 간단한 3층 신경망 손계산으로 직접 보여 준 뒤, 같은 구조에 스킵 커넥션을 추가했을 때 기울기가 어떻게 달라지는지 비교하며 ResNet의 핵심 아이
inner-game.tistory.com
이 블로그의 관련 글
[AI 인공지능 머신러닝 딥러닝] - AI 공부하는 순서
AI 공부하는 순서
여기 나오는 것 중에 모르는 것이 없어야 함. 기초중의 기초.[AI 인공지능 머신러닝 딥러닝/인공지능 수학] - LEVEL 0: AI를 위한 기초 수학 | 혁펜하임 LEVEL 0: AI를 위한 기초 수학 | 혁펜하임LEVEL 0: AI
inner-game.tistory.com
'AI 인공지능 머신러닝 딥러닝/딥러닝' 의 관련글
-
딥러닝 101 - 8강. 확률적 경사하강법을 소개합니다 | Deep Learning 101 2026.01.09더보기
-
딥러닝 101 - 7강. Cross Entropy 크로스엔트로피 손실함수를 알아보자 | Deep Learning 101 2026.01.09더보기
-
딥러닝 101 - 5강. LSTM, 초보자를 위한 안내서 | Deep Learning 101 2026.01.09더보기
-
딥러닝 101 - 3강. 순환신경망 RNN, Recurrent Neural Networks | Deep Learning 101 2026.01.09더보기





