2025 인공지능·머신러닝 입문자를 위한 핵심 통계개념 완전정복 (1/2)
안녕하세요! 오늘은 최근에 시청한 유튜브 신박Ai의 “[인공지능을 위한 머신러닝101] 머신러닝을 위한 기초통계개념” 영상을 바탕으로, 인공지능과 머신러닝을 공부하는 데 꼭 필요한 통계 개념들을 정리해보았습니다. 머신러닝이나 데이터과학, 인공지능을 처음 접하는 분들에게 도움이 되면 좋겠습니다.
이 포스팅은 전반부 강의 내용 입니다.

https://youtube.com/playlist?list=PLW2RwdZfXkE9rjbyxetoxDfEx9vCvUIV2&si=vy-NMTGyoRkrtG63
인공지능을 위한 머신러닝 101 - 간단 정리
이번 영상에서는 머신러닝을 이해하기 위한 9가지 핵심 통계개념이 소개됩니다.
아래는 각 개념의 요약입니다.
변수(variable)
변하는 값, 숫자로 표현되고 상황에 따라 달라질 수 있는 모든 요소
예: 농부의 수확량, 마을 인구수, 논의 넓이
변량(variate)
변수의 실제 데이터 값들
예시) 10년의 수확량 데이터: 300kg, 500kg, 700kg 등
평균(mean)
변량의 합계 나누기 개수
데이터의 전체적인 “중심”을 나타냄
분산(variance)
각 변량이 평균에서 얼마나 떨어져 있는지
차이값의 제곱 평균
표준편차(std. deviation)
분산의 제곱근
직관적으로 데이터가 평균에서 얼마나 벗어나는지 판단
정규분포(normal distribution)
평균을 중심으로 대칭적인 종모양의 분포
자연현상, 인간 행동 등 많은 데이터가 이를 따름
독립변수(independent variable)
다른 값을 변화시키는 변수
예: 비료 양, 날씨
종속변수(dependent variable)
독립변수에 따라 값이 바뀌는 변수
예: 수확량 (비료의 양에 따라 달라짐)
p-값(p-value)
실험 결과가 우연히 나타날 확률
p값이 작으면 대립가설을 채택(인과관계가 있을 가능성 높음)
통계 개념을 통한 머신러닝 이해
강의에서는 옛날 농부의 사례로 통계 개념들을 쉽게 비유해줍니다.
농부는 수확량이 해마다 달라지는 것을 보고 수확량(변수)에 관심을 갖습니다. 10년치 데이터를 모아 평균, 분산, 표준편차를 계산해봅니다. 그리고 수확량이 평균 근처에 모여있는 정규분포 형태임을 파악합니다.
여기서 날씨·비료·씨앗질 같은 독립변수가, 최종 수확량(종속변수)에 영향을 미친다는 점도 심층적으로 설명됩니다. 핵심은 데이터 속에 숨어있는 인과관계와 상관관계, 그리고 이를 통계적으로 검증하는 과정에서 p값의 역할입니다.
특히 강의 후반에서는 가설 검정에서 ‘귀무가설’과 ‘대립가설’을 구분하고, p값(통계적 유의성)이 과학적 결론에 어떻게 적용되는지를 설명합니다.
예를 들어 비료를 많이 준다고 해서 수확량이 항상 늘어나는 것은 아니며, 여러 조건들을 고려해 확률적으로 인과관계를 판별해야 하는 이유를 사례로 들어 이해시키는 점이 인상적이었습니다.
인공지능 및 머신러닝 구조와 응용
신경망, CNN, 트랜스포머 등 최신 딥러닝 모델 소개
모델 평가, 분류/회귀 적용 실습
실제 데이터 사례 기반 머신러닝 워크플로우
배운 점 & 후기
머신러닝을 배우는 입장에서는 통계의 기본개념을 반드시 알고 넘어가야 합니다.
평균·분산·표준편차는 데이터의 특성을 파악하는 데 필수이고, 정규분포·독립·종속변수는 데이터 해석과 모델 구현 시 기초가 됩니다.
또 가설 검정과 p값 개념은 실제 인공지능 모델 평가지표에도 활용됩니다.
신박Ai의 강의는 어려운 개념도 알기 쉽게 예시와 비유로 풀어주기 때문에, 누구나 ‘데이터를 과학적으로 보는 시각’을 기를 수 있습니다. 앞으로 더 심화된 머신러닝/딥러닝 강의도 기대됩니다!
강의 목록 및 내용 정리 (머신러닝101 주요 콘텐츠)
1. [인공지능을 위한 머신러닝101] 머신러닝을 위한 기초통계개념들을 소개합니다

평균 , 뮤 = 533,6
머신러닝과 통계에서 강의에 나오는 개념들은 그리스 문자와 영어 용어를 사용해 국제적으로 표준화되어 있습니다. 평균은 μ (mu, 발음: myoo) 또는 x ˉ (x-bar)로, 전체 모집단 평균을 나타내며 영어로는 "mean" 또는 "population mean"이라고 합니다.

분산은 σ 2 (sigma squared)로 표기되며 영어로 "variance" 또는 "population variance"입니다.

표준편차는 σ (sigma)로, 분산의 제곱근이며 "standard deviation" 또는 "population standard deviation"이라고 합니다.
샘플 데이터의 경우 각각 s^2(제곱) 와 s 를 사용합니다.

정규분포와 p-값 정규분포는 종 모양 곡선으로 N ( μ , σ^2 ) 로 쓰며, 영어로 "normal distribution" 또는 "Gaussian distribution"입니다.

독립변수는 X로, 종속변수는 Y로 자주 쓰이며 영어로는 "independent variable"과 "dependent variable"입니다. 상관관계는 "correlation"으로, 인과관계와 구분됩니다
p가 0.03이면 '비료 안준밭'의 수확량이 우연히 증가할 확률이 3%

p-값은 "p-value"로 표기되며 가설 검정에서 귀무가설이 참일 때 관찰 결과의 확률을 의미합니다


과학적 보수주의 때문에.

| 한국어 용어 | 영어 용어 | 기호 | 발음 |
| 평균 | Mean | μ | 뮤 |
| 분산 | Variance | σ2 | 시그마 skwaird |
| 표준편차 | Standard Deviation | σ | 시그마 |
관련 내용 포스트(조금 더 수학 수식적으로 접근하고 싶다면..)
[AI 인공지능 머신러닝 딥러닝/인공지능 수학] - LEVEL 0: AI를 위한 기초 수학 | 혁펜하임
LEVEL 0: AI를 위한 기초 수학 | 혁펜하임
LEVEL 0: AI를 위한 기초 수학 재생목록은 딥러닝·머신러닝을 막 시작하는 학습자들이 꼭 알아야 할 최소한의 수학을, 하나의 코스로 정리해 둔 재생목록입니다.함수·극한·미분부터 확률과 분포
inner-game.tistory.com
2. [인공지능을 위한 머신러닝 101] 선형회귀란 무엇인가?
선형회귀(Linear Regression)는 집 크기(x)와 가격(y)처럼 독립변수와 종속변수 간 직선 관계를 모델링하며, 기본 방정식은 y=mx+b입니다. 여기서 m은 기울기(slope), b는 절편(intercept)으로 불립니다
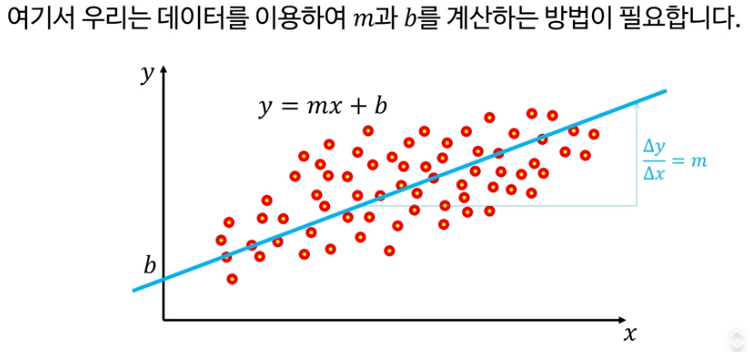
경사 하강법

비용함수는 예측한 값과 실체값의 차이를 측정하는 함수
경사하강법에서 핵심내용은 비용함수 입니다.
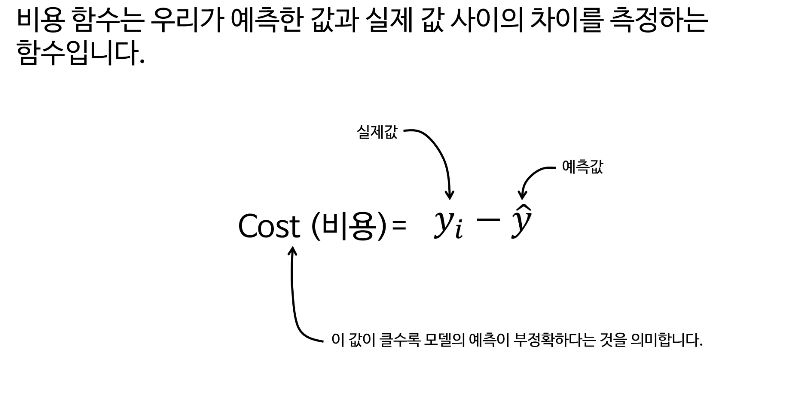
경사하강법(Gradient Descent"그라디언트 디센트")은 비용함수(cost function)의 최저점을 찾기 위해 매개변수(m, b)를 반복 업데이트하합니다.

비용함수는 평균제곱오차(MSE, Mean Squared Error)로 U자 모양(parabolic bowl)의 손실 함수(loss function)를 의미합니다.

'경사하강법 및 손실함수에 대한 자세한 내용'은 아래 포스팅의 '8. 경사하강법' 참고하세요
[AI 인공지능 머신러닝 딥러닝] - 2025 인공지능 기초 완전정복: 유튜브로 배우는 신경망·딥러닝·실습코딩 가이드
2025 인공지능 기초 완전정복: 유튜브로 배우는 신경망·딥러닝·실습코딩 가이드
안녕하세요! 오늘은 제가 최근에 시청한 유튜브 플레이리스트 “인공신경망기초-신박Ai”를 바탕으로, 인공지능(Artificial Intelligence; AI) 기초에 대해 공부한 내용을 정리하여 티스토리 블로그 포
inner-game.tistory.com
기울기 하강법 손계산 해보기
초기값을 아래 파란선으로 설정하고, 최적의 값을 찾는 과정

아래 수식의 첫째줄
이걸로 평균 제곱 오차(MSE)를 구했더니 11.125
두번째 줄은 원래의 MSE 공식이고
그 아래는 그냥 풀어준것
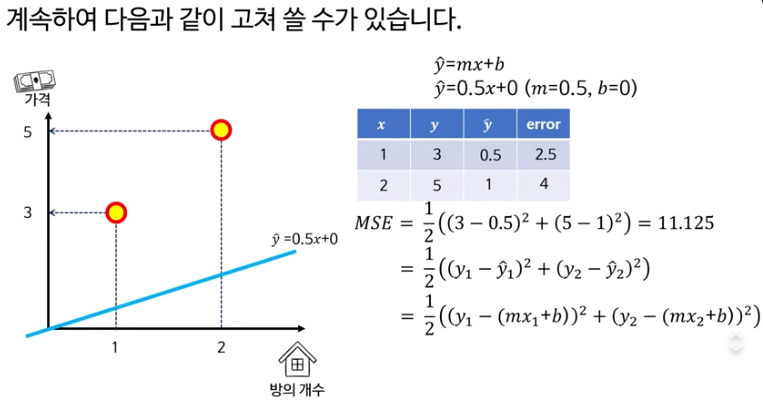
손실함수 리마인드

MSE 리마인드

MSE를 오차의 합으로 하는 이유는 데이터가 2개(y₁, y₂)라서 손실함수도 “두 점의 오차를 모두 반영한 하나의 숫자”가 되어야 해서 그렇게 정의합니다. 한 점만 쓰면 그 점에만 잘 맞고 나머지 데이터는 완전히 무시되기 때문에, 보통은 모든 샘플의 오차를 더해서(또는 평균 내서) 손실을 만듭니다.

손실이 최소가 되는 지점을 찾는것이 목표이다.
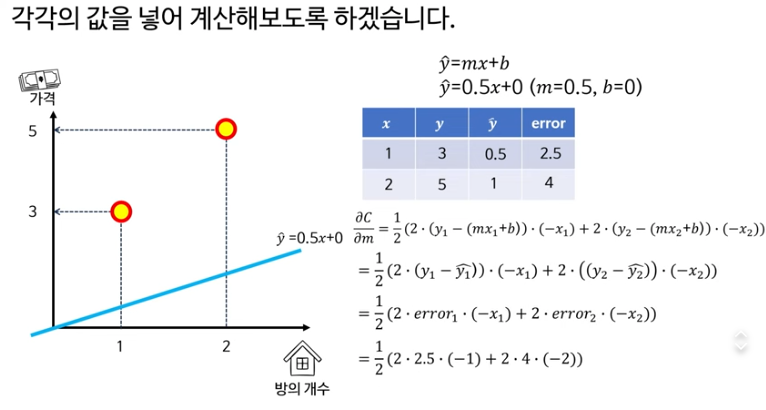
−10.5는 지금 기울기m(0.5)에서 손실 C를 m방향으로 미분한 값(gradient)이고, “기울기를 조금 키우면 손실이 얼마나 변하는지”를 뜻합니다.
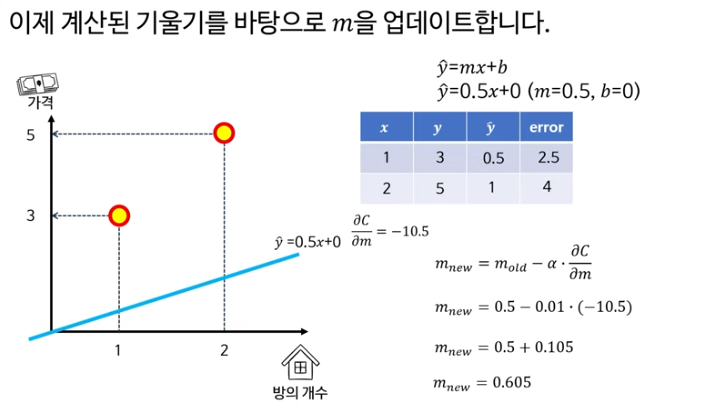
α: 러닝 레이트, 한 번에 얼마만큼 움직일지 정하는 “스텝 크기(step size)”
α가 크면 한 번에 많이 움직여서 빠르게 내려가지만, 너무 크면 최소점을 지나쳐서 튈 수 있고
α가 너무 작으면 안정적이지만 학습이 아주 느려지는 거라서, 적당한 값을 실험으로 정하는 게 일반적입니다.
바이어스 b도 업데이트 해주어야 한다.

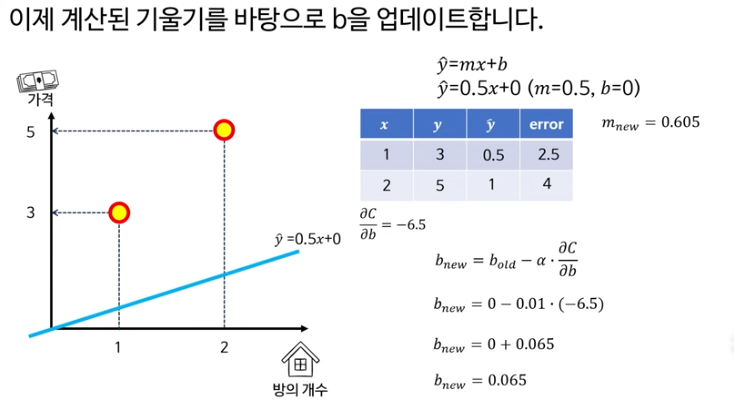
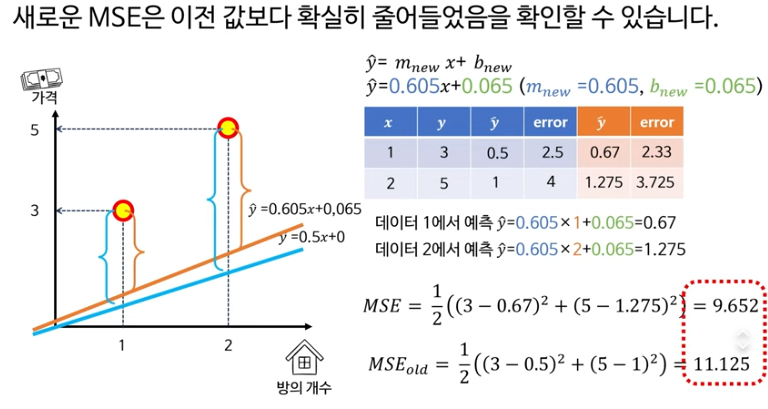
이런식으로 반복적으로 계산하여 MSE가 최소가 되는 m과 b를 찾는것이 경사하강법이다.
선형회귀에서 등분산성은 중요하다.
등분산성(Homoscedasticity)은 잔차의 분산이 x 값에 따라 일정해야 하는 선형회귀 가정으로, 영어 발음은 "호모스케다스티시티"입니다. 분산이 불균등하면(heteroscedasticity) 예측 신뢰도가 떨어집니다.
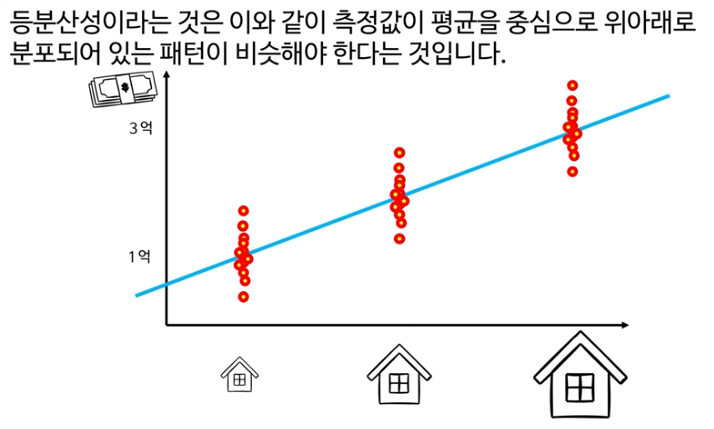
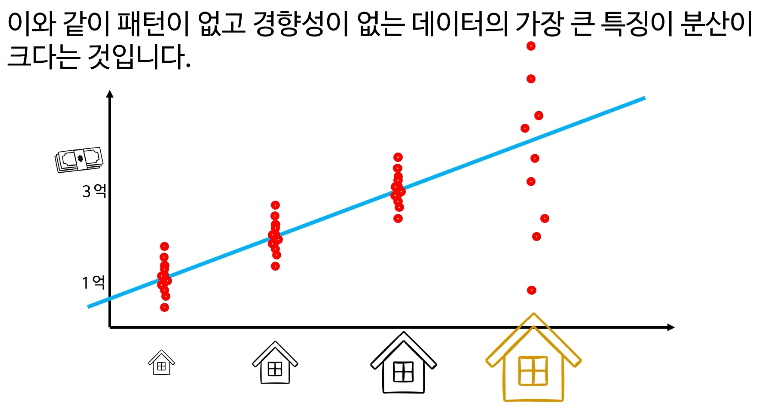
그러므로 분산이 동일, 혹은 비슷한 경우에 선형회귀의 예측력이 타당하다고 할 수 있다.

| 한국어 용어 | 영어 용어 | 기호/설명 | 영어 발음 |
| 선형회귀 | Linear Regression | y=mx+b | 리니어 리그레션 |
| 기울기 | Slope | m (또는 β1) | 슬로프 |
| 절편 | Intercept | b (또는 β0) | 인터셉트 |
| 경사하강법 | Gradient Descent | θ←θ−α∇J(θ) | 그래디언트 디센트 |
| 비용함수 | Cost Function | J(m,b) | 코스트 펑션 |
| 평균제곱오차 | Mean Squared Error (MSE) | 1/n∑(yi−yi^)2 | 민 스퀘어드 에러 |
| 등분산성 | Homoscedasticity | 잔차 분산 일정 | 호모스케다스티시티 |
3. [인공지능을 위한 머신러닝 101] 로지스틱 회귀란 무엇인가?
비어있는 값을 예측 -> 선형회귀로 가능
분류(예:이진분류,암발병 유무) -> 선형회귀로 불가능, 극단적인 데이터가 바뀌면 평균이 바귀는것 같은 원리 때문.
아래에서 실제 암인데도 암이 아닌것으로 분류된 해골근처 데이터

그래서 S자 형태의 확률분포를 생각해냈다.
시그모이드 확률분포를 p(x) 라고 한다면, x와 p(x)의 관계는 시그모이드함수


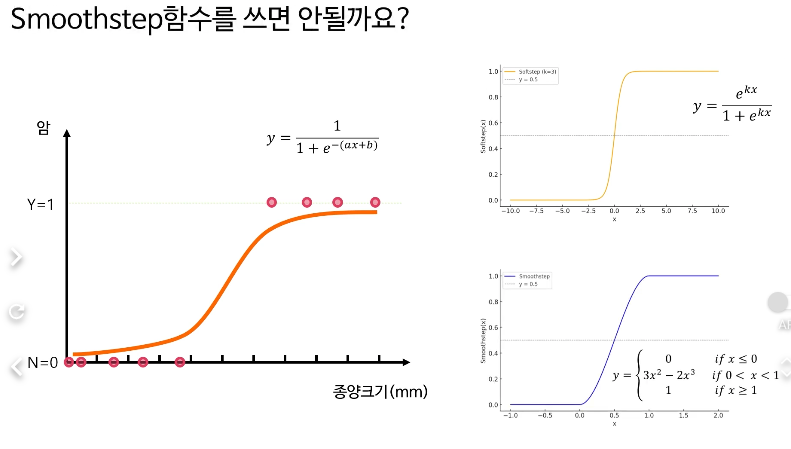
아래에 왜 꼭 시그모이드 여야 하는지 이유가 나온다.

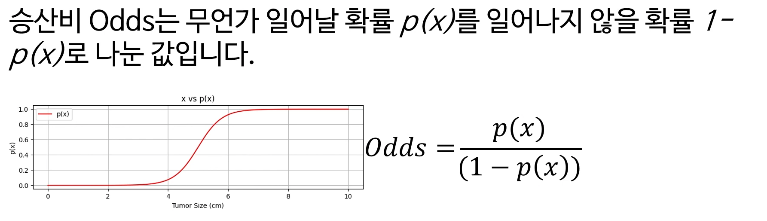




로지스틱 회귀 Logistic Regression이라는 이름 자체가, 로짓과 선형함수의 관계속에서 이 두이름을 합친 것.

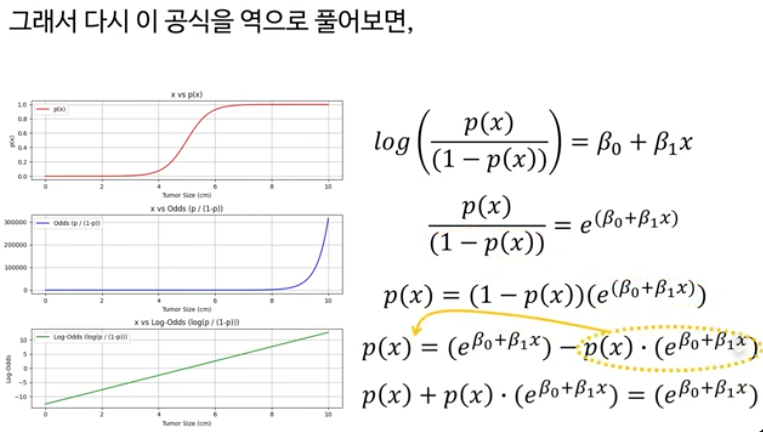
여기서 log 는 자연로그(밑이 e)라서 ln과 같다
자연로그 log의 역함수는 지수함수 e (⋅)
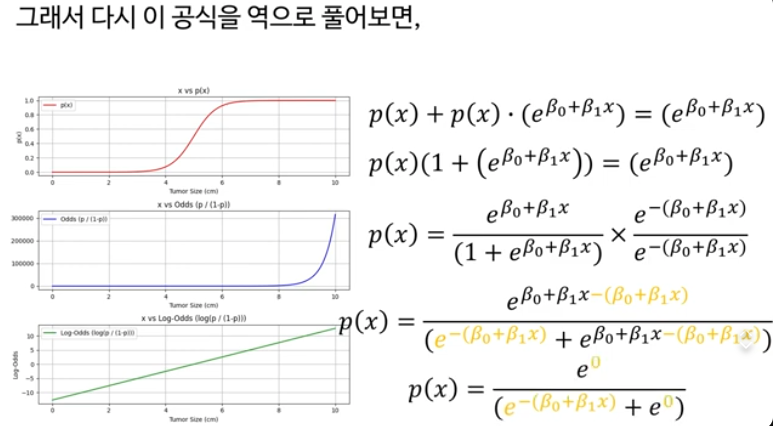

이렇게 정리한 이유

은 “두 개의 지수항을 정규화한 비율” 형태라서,
- 분자는 클래스 1의 스코어(여기서는 0),
- 분모는 두 클래스 스코어의 지수 합
처럼 보이게 돼서 소프트맥스 형태와 완전히 같은 구조가 됨.
“지수의 합으로 나눈다”는 소프트맥스 관점을 강조하려고 분자·분모에

를 곱해서 저 모양으로 바꿔준 것.
여기서 “클래스”랑 “스코어”는 로지스틱 회귀를 “2클래스 소프트맥스”로 해석할 때 쓰는 표현
클래스(class)
로지스틱 회귀는 보통 이진 분류를 할 때 쓰니까, 아래의 두 개의 클래스를 가정.
- 클래스 0: 음성 클래스 (예: 고장 아님, 스팸 아님)
- 클래스 1: 양성 클래스 (예: 고장, 스팸)
스코어(score)
스코어는 “각 클래스에 대해 모델이 계산한 실수값”이야.
- 일반적인 소프트맥스에서는 클래스 k마다 스코어

를 만들고, 확률은

로 정의.


로지스틱스 회귀의 최적화 과정을 Step-by-Step으로 알아보기
1. 문제를 간단하게 하기 위해 베타0 과 베타1은 0으로 초기화

2. 그 다음 차례: 손실함수를 활용하여 손실 Loss를 구할 차례
손실함수는 크로스엔트로피를 활용하여 구하도록 합니다.
2.77이 된다.

3. 경사하강법을 활용하여 새로운 파라미터 b0, b1을 구한다.
먼저 손실함수 L을 b0에 대해 미분하면 다음과 같이 됩니다.

미분 1단계

미분 2단계

미분 3단계

위 두개를 대입하면 최종적으로,


참고: 시그모이드와 표준편차의 기호는 모두 시그마





편미분한 값은 각각 0, -5.5가 나온다.

러닝레이트 기호 η는 그리스 문자 “eta(에타)”
한국어: “에타”
영어: “에이타 / 에타” (보통 eta 라고 발음)
b0과 b1을 시그모이드 수식에 넣어준다.


4. [인공지능을 위한 머신러닝 101] 서포트 벡터 머신에 대해 알아보자!
분류와 회귀 모두에 사용되는 알고리즘
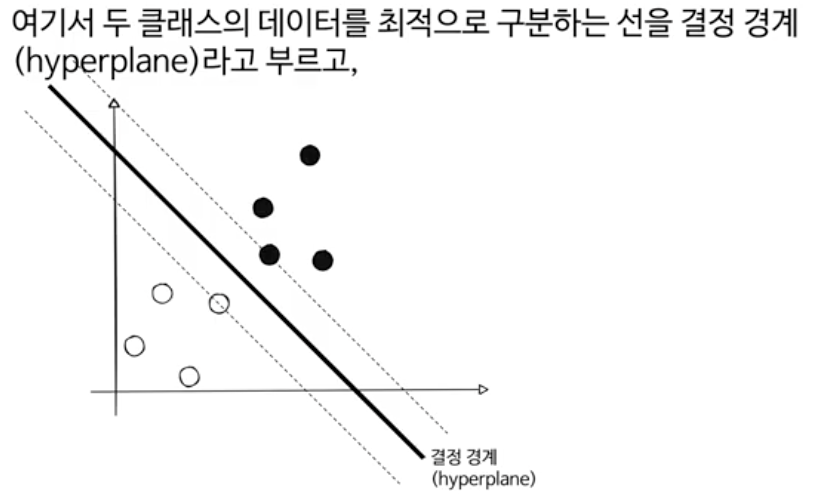
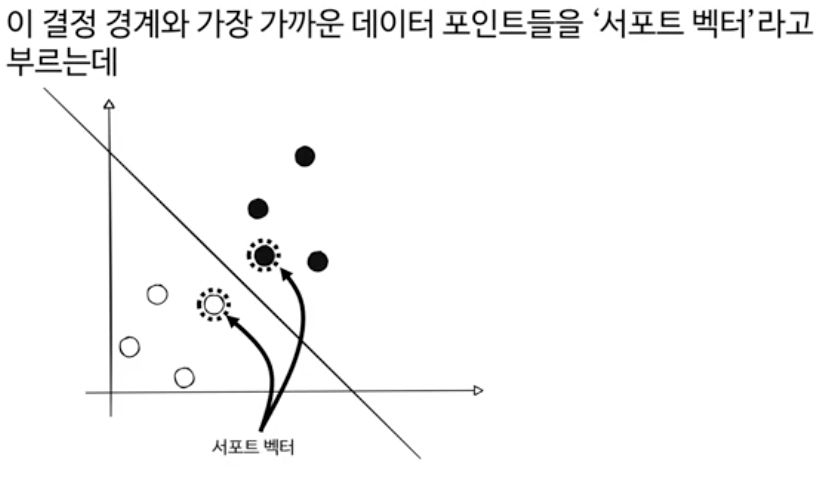
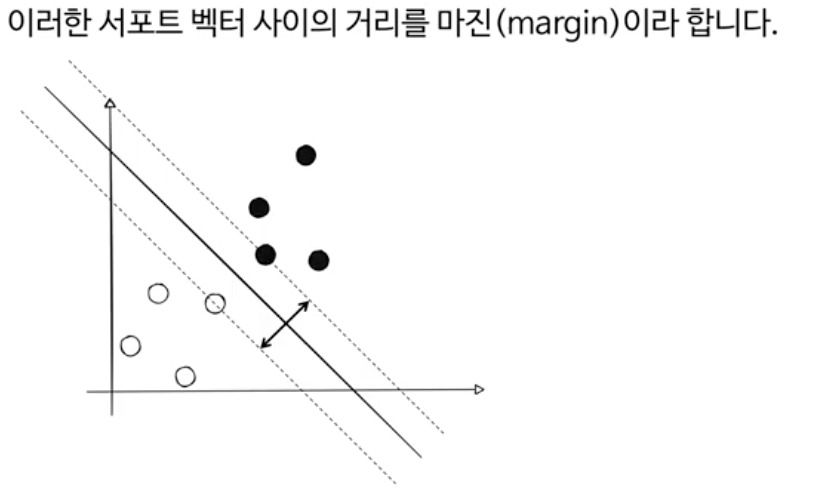

마진을 >=1, <= -1로 둔것은 그냥 계산을 편리하기 위해서 설명용으로 설정한것
그리고 이를 바탕으로, 마진의 크기를 구했다. 2/||w||
SVM 벡터 표현 이해하기


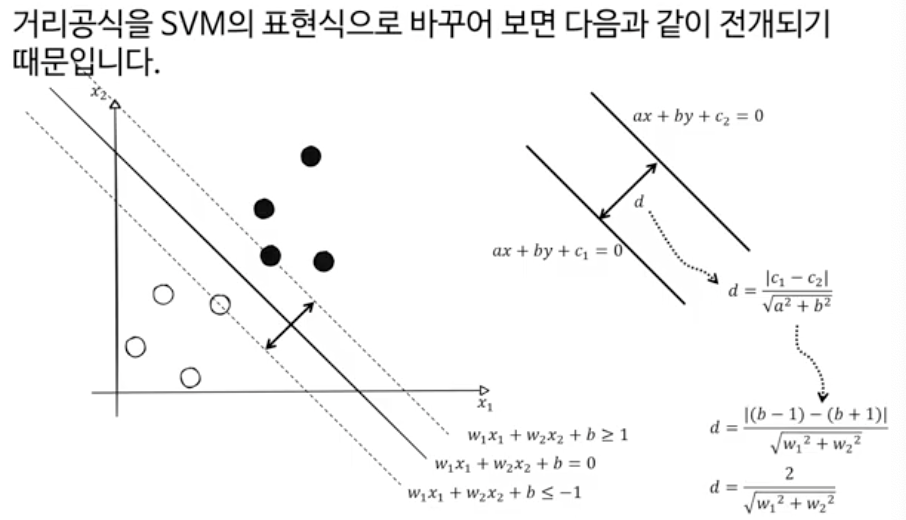
원래 벡터의 기울기는 y = ax + b에 의해 ax + b = 0은 -a/b가 되지만, 직교하는 벡터의 경우에는 기울기가 a/b가 된다.



위의 공식에 ax+by+c = 0의 ax + by = -c를 대입해주면 분자가 |-c+c| 이 되어 공식이 성립한다.

거리 d = 2 / || w ||
이때 분모인 w벡터 크기, 즉 벡터 놂이 작아지면 거리 d가 커진다.
|| w || 를 최소화 하려고 하는데, 미분의 특성상 계산의 편의를 위해 1/2 || w || 제곱 이라고 둠.
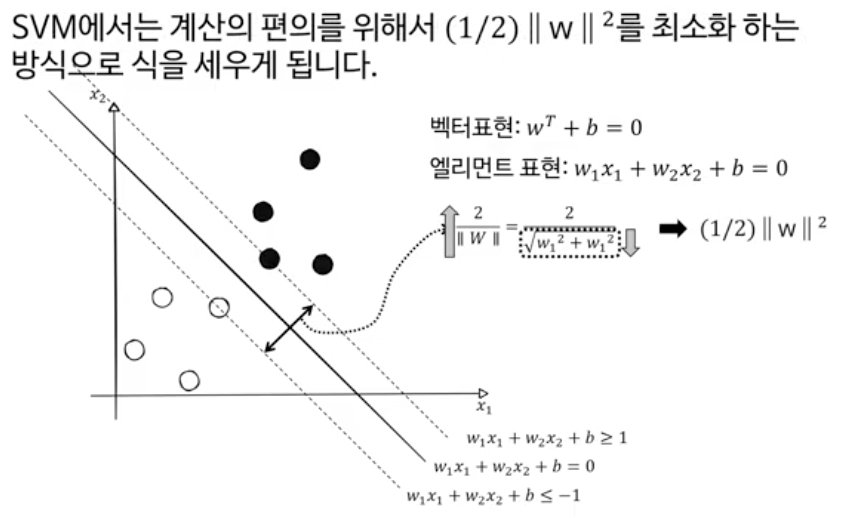
SVM에서 w가 작아질수록 마진이 커지는 이유는 마진(margin)이 초평면(하이퍼플레인)과 서포트 벡터들 사이의 거리이고, 이 거리는 2/∥w∥로 정의되기 때문입니다. 즉, 마진 값은 1/∥w∥에 비례하므로, w의 크기 ∥w∥가 작아지면 분모가 작아져 마진은 커지게 됩니다. 반대로 w가 커지면 마진은 작아집니다.
여기서 1/2∥w∥제곱는 SVM의 목적 함수에서 최소화하려는 항으로, 이는 ∥w∥제곱를 작게 만들어 마진을 최대화하는 것과 같습니다. 즉, 1/2∥w∥제곱를 최소화하는 것이 마진 ∥w∥제곱를 최대화하는 것과 동일한 목표를 가집니다.
요약하면:
- SVM 마진 = 2∥w∥2마진을 최대화하려면 ∥w∥를 최소화해야 함
- 최적화 문제로는 1/2∥w∥2(제곱)를 최소화함으로써 마진을 최대화하는 효과를 얻음
- 따라서, w의 크기가 작아질수록 마진은 커지게 되는 것입니다.

첫번째식 1과 같거나 크다, 두번째식 -1보다 같거나 작다.
+1 의 나라가 y = +1
-1의 나라가 y = -1
여기서 y는 “데이터셋에 원래 붙어 있던 클래스 라벨”이야. 갑자기 생긴 변수가 아니라, 각 샘플마다 yᵢ∈{+1,−1} 이라고 처음부터 가정한 것. 모델을 정할 때 편의를 위해 사람이 정한 규칙(스케일 선택) 임.
2, -2 혹은 3, -3 으로 정의해도 결국 수학적으로는 같은 결론에 도달한다.
y(엘리먼트식) = +1(엘리먼트식) 이라는 것의 양변에 (엘리먼트 식)을 각각 곱한것


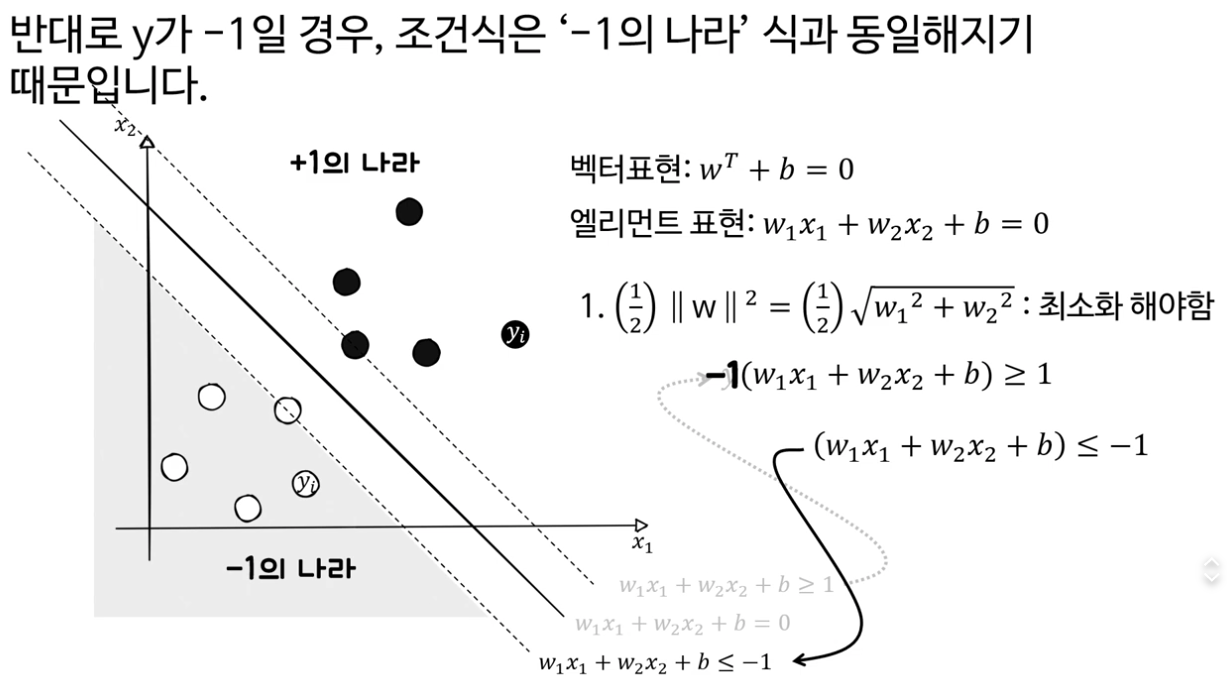

위의 1,2번 식의 의미
1번식은 마진의 크기를 보여주는것, 최소화해야함. 이것이 SVM의 주된 목적
하지만 마진이 너무 크면 2번에 위배되기 시작함

라그랑주 승수법
이러한 제약조건이 있는 최적화 문제를 일반적인 방법으로 풀기 어렵기 때문에, 제약 조건과 목적함수를 함께 고려할 수 있는 라그랑주 승수법 이라는 수학적 기법을 사용하여 해결한다.

두번째 항은, 제약 조건을 만족하는 정도,

우리는 이 식을 풀어서 과연 SVM이 결정경계를 확정할 수 있는지를 알아보도록 하겠습니다.
손계산을 간단히 하기 위해, 두 개의 서포트 벡터만 가정하여 계산하도록 하겠습니다.


KKT 조건은 “제약이 있는 최적화 문제에서, 최적해가 되려면 반드시 만족해야 하는 미분 조건들”
1. Stationarity(정지 조건): 정지 조건 ∇ w L = 0 , ∇ b L = 0 (stationarity)
2. Primal feasibility(원 문제 제약 만족)
3. Dual feasibility(라그랑주 승수 조건): 라그랑주 승수의 비음수성 α i ≥ 0 (dual feasibility)
4. Complementary slackness(상보 느슨성): 상보적 느슨성 αi [ yi ( w⊤ xi + b ) − 1 ] = 0



w1=w2=2a가 된다는것을 알수있다.
아래는, 이 아래 그림의 검은 점선사각형 = 0 에 대한 설명입니다.
슬라이드에서 >=0 이 아닌, =0 이라고 한 건 “마진 위에 딱 붙어 있는 support vector들에 대해서만 보고 있기 때문”이야.
2. Primal feasibility(원 문제 제약 만족)
4. Complementary slackness(상보 느슨성)
"제약에서 벗어나는 점이 없게, 가장 빡빡하게 y_i(w⋅x_i + b)-1 = 0이 되도록 보는 것”
즉, α i >0인 서포트벡터에 대해 y i ( w ⊤ x i + b ) − 1 = 0 이라고 두는 것
KKT에서는 제약조건에서 벗어나는 점이 없어야 합니다.
그래서 각각의 제약조건이 제일 작은 0이 된다고 할수 있는데, 그 이유는 아래와 같습니다.



아래의 대각선 x2 = -x1이 두 클래스를 최적으로 분류하는 결정경계선이다.


실제 머신러닝에서는
라그랑주 함수를 변형하여, 이차계획법 이라는 수치적 최적화 기법으로 풀고,
일반적인 수치 해석 최적화 기법(예:SMO 알고리즘, interior-point method 등)을 사용해 컴퓨터가 수치적으로 a값을 계산합니다.


선형분리가 불가능한 데이터는 어떻게 해야할까?



커널트릭을 손계산해서 알아보자
3차원에 저 제곱+제곱 값을 넣으면 확실히 두 클래스가 구분 가능해 진다.(위의 오른쪽 그림)

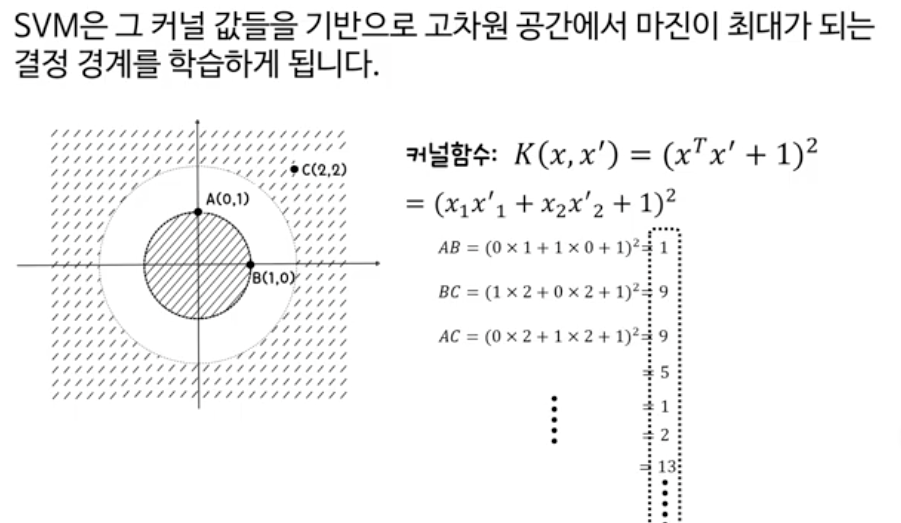
실제 커널함수는 점 하나 즉 (x1, x2) 벡터 하나를 계산하는 것이 아니라, (x'1, x'2)의 두개의 벡터(점)의 유사성을 구하기 위해 고차원으로 변환하는 것이 바로 커널함수입니다.
이 두 점간의 관계를 가장 간단히 계산할 수 있는 커널 함수가 바로 다항커널 입니다.


다항 커널함수{ k(x,x')=(xTx+1)제곱 }의 의미는,

다항 커널함수의 의미는, '단순히 두 점을 벡터곱(내적)하면, 간단한 스칼라 값(실수값, no벡터)이 되고, 거기에 c상수를 더해서 그 값(여전히 스칼라)을 단순히 제곱하는 것만으로, 2차원에 존재하는 점들을 6차원으로 바꾸는 것인데..(아래 그림 참조)', 이 계산 결과가 6차원 벡터(파이)를 벡터곱인 함수 값과 동일한 값을 갖는 것을 의미한다.
ϕ(Φ)는 영어로 보통 파이 (phi, 발음: /faɪ/, “fai”)




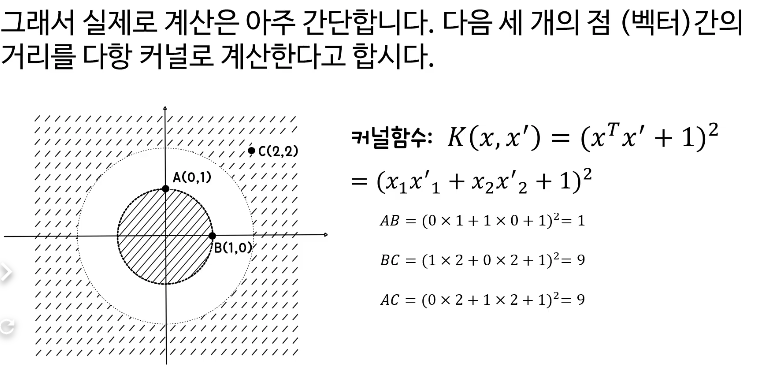
이런식으로, 아래의 세 점 말고도, 클래스 내외의 모든 점들 간의 커널함수 값을 계산한뒤,


[AI 인공지능 머신러닝 딥러닝] - 커널 트릭 설명 | Kernel Trick의 개념적 이해
커널 트릭 설명 | Kernel Trick의 개념적 이해
관련 영상 총 4개에 대한 리뷰입니다. 커널 트릭이라는 말이 어렵게 느껴지지만, 아이디어 자체는 직관적이에요. 우리는 보통 데이터를 직선이나 평면으로 나누려고 합니다. 예를 들어 2차원 좌
inner-game.tistory.com
여기까지입니다.
이어서 후반부의 내용은 아래의 포스팅을 참고하시면 됩니다.
[AI 인공지능 머신러닝 딥러닝] - 2025 인공지능·머신러닝 입문자를 위한 핵심 통계개념 완전정복 (2/2)
2025 인공지능·머신러닝 입문자를 위한 핵심 통계개념 완전정복 (2/2)
안녕하세요! 오늘은 최근에 시청한 유튜브 신박Ai의 “[인공지능을 위한 머신러닝101] 머신러닝을 위한 기초통계개념” 영상을 바탕으로, 인공지능과 머신러닝을 공부하는 데 꼭 필요한 통계 개
inner-game.tistory.com





