딥러닝 101 - 5강. LSTM, 초보자를 위한 안내서 | Deep Learning 101

이 영상은 LSTM이 등장하게 된 배경부터 구조·순전파·역전파 알고리즘까지, “왜 이렇게 설계됐는지”를 직관과 수식으로 함께 풀어 주는 이론 중심 강의입니다. 특히 RNN의 장기 의존성 문제와 LSTM의 셀 상태·게이트 메커니즘을 연결해 설명해 주기 때문에 입문자에게도 맥락이 잘 잡히는 구성입니다. ​ ​ 

 

 

딥러닝 101

 

 

[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 무료 강의 전체 소개 | Deep Learning 101

딥러닝 101 - 무료 강의 전체 소개 | Deep Learning 101

 

 

 

 

 

 

 

LSTM이 탄생한 배경: 장기 의존성 문제 

강의는 먼저 기본 RNN의 역전파 수식을 다시 꺼내와, 시간 축이 길어질수록 체인 룰로 곱해지는 항들이 1보다 작은 값이라면 기울기가 0에 가까워지는 현상을 보여 줍니다. 이로 인해 문장 번역에서 “Don’t … underestimate your inner strength” 같은 문장에서, 의미상 짝을 이루는 “Don’t–마세요”처럼 멀리 떨어진 단어들 사이의 의존성이 잘 학습되지 않는다는 예시를 듭니다. ​ ​ 

 

이렇게 시간적으로 먼 정보가 학습에 거의 기여하지 못하는 현상을 장기 의존성 문제라 부르고, 이를 해결하기 위한 RNN의 변형으로 LSTM(Long Short-Term Memory) 이 제안되었다는 역사적 맥락을 간단히 짚어 줍니다. ​ ​ 

 

 

 

 

 

 

 

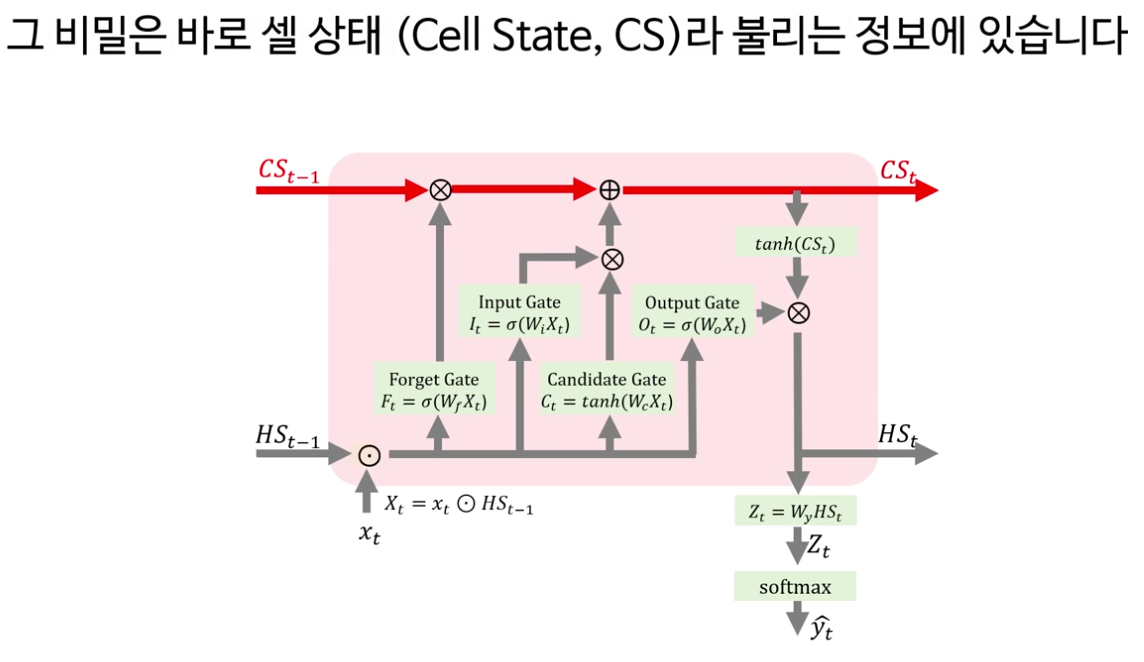
LSTM의 구조와 셀 상태의 역할 

다음으로 강의는 LSTM의 핵심을 “셀 상태(cell state)와 네 개의 게이트”로 정리합니다. LSTM은 기본적으로 RNN처럼 시계열 데이터를 처리하지만, 내부에 장기 기억에 해당하는 셀 상태 C t 와 보다 단기적인 정보를 담는 은닉 상태 h t 두 흐름을 동시에 유지한다는 점이 강조됩니다. ​ ​ 

 

 

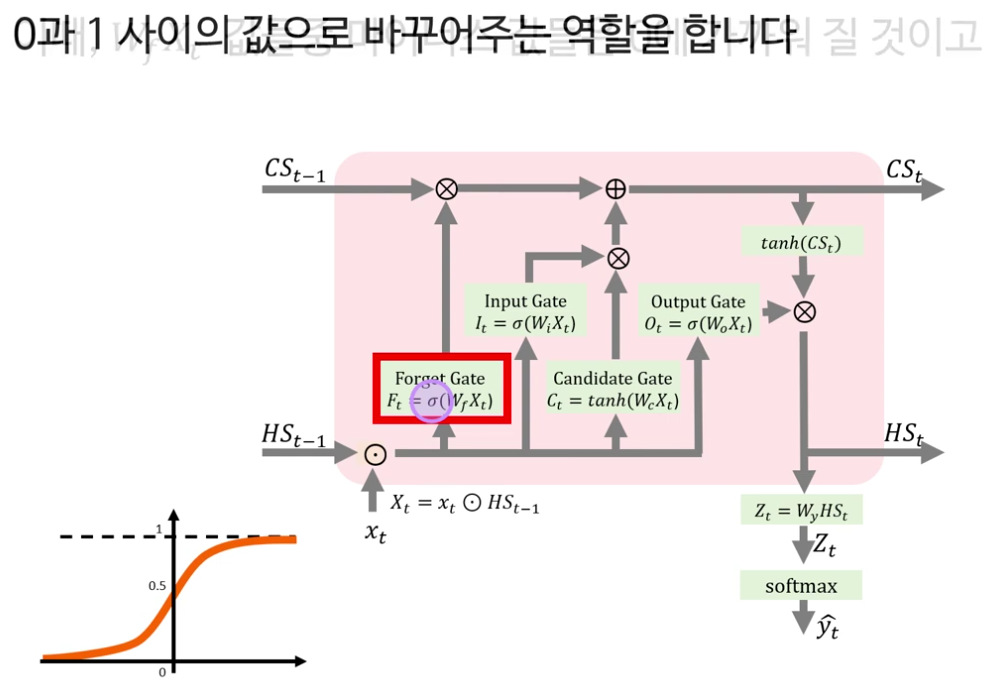
· Forget 게이트: 이전 은닉 상태 h t−1 와 현재 입력 x t 를 concat한 벡터에 가중치 W f 를 곱하고 sigmoid를 취해, 0~1 사이의 값으로 “무엇을 얼마나 지울지”를 결정합니다. 이 값이 셀 상태 C t − 1 C t−1 와 원소별 곱(element-wise)으로 결합되며, 0에 가까운 위치의 정보는 잊혀지고 1에 가까운 위치의 정보는 유지됩니다.

 

 

 

 

 

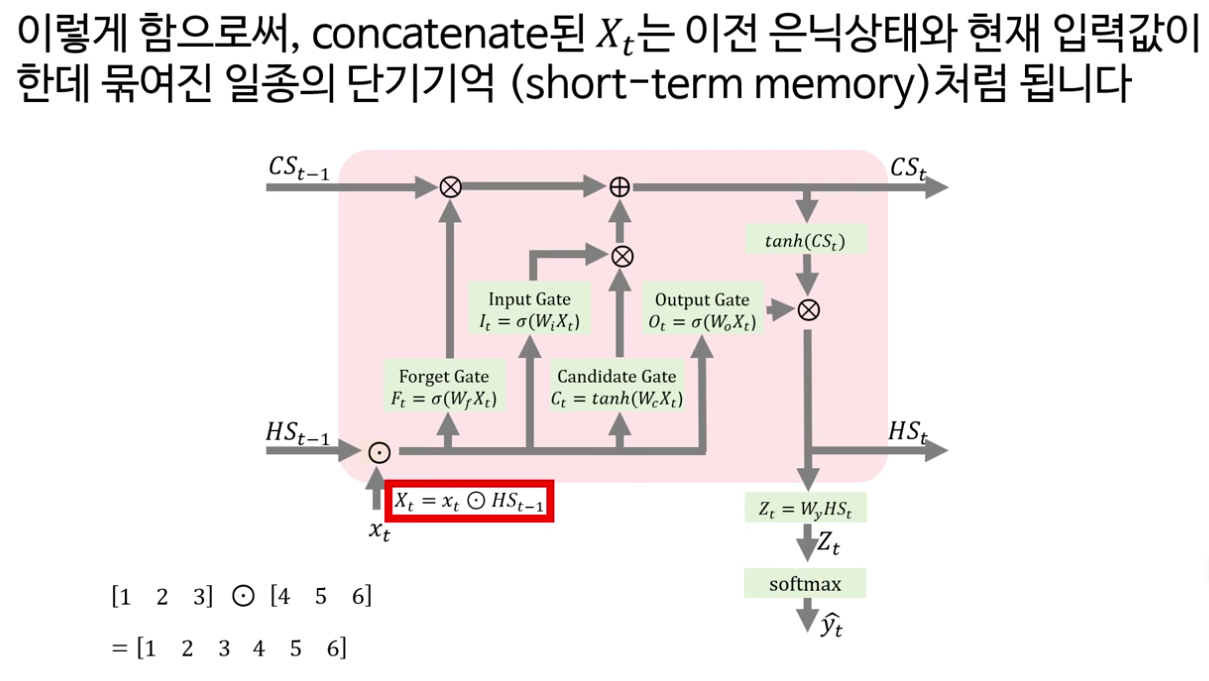
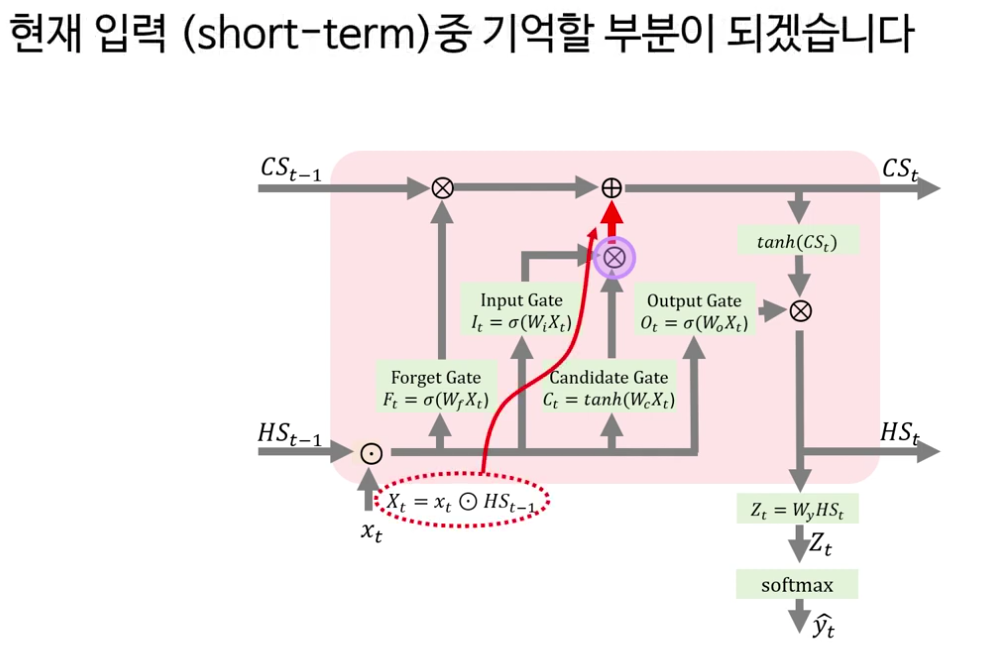
· Input 게이트와 Candidate 게이트: Input 게이트는 forget 게이트와 동일하게 sigmoid를 통해 “무엇을 새로 쓸지”를 결정하고, Candidate 게이트는 tanh를 통해 −1과 1 사이의 후보 정보 C ~ t 를 만듭니다. 두 출력의 원소별 곱을 통해 “현재 입력 중 기억할 부분”만 추려 셀 상태에 더해 장기 기억을 업데이트합니다.

 

 

 

 

· Output 게이트: 업데이트된 셀 상태 C t 를 tanh로 스케일링한 뒤, output 게이트의 sigmoid 출력과 원소별 곱을 해 새로운 은닉 상태 h t 를 만듭니다. 이 h t 는 셀 상태보다 더 단기적인 특성을 반영하며, 다음 시점의 입력이자 최종 출력층에 전달되는 특징 벡터로 사용됩니다.

 

 

 

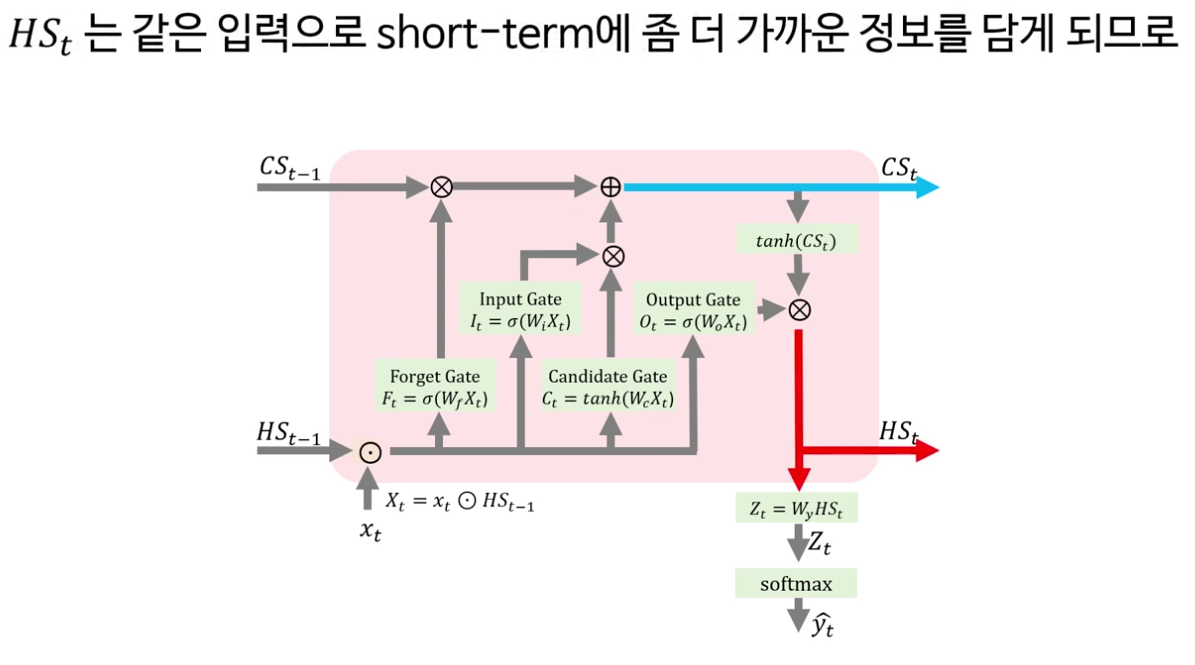
이 과정을 통해 LSTM은 셀 상태에 비교적 장기적인 정보를, 은닉 상태에 단기적인 정보를 담으면서, RNN보다 훨씬 안정적으로 긴 시퀀스를 다룰 수 있는 구조를 갖추게 됩니다. ​ ​

 

 

 

 

 

 

숫자로 따라가는 순전파 계산

영상의 중반부에서는 히든 차원을 2, 입력 차원을 3으로 두고, 가중치 행렬과 입력 시퀀스를 구체적인 숫자로 설정한 뒤 LSTM 한 타임스텝의 순전파를 끝까지 계산해 나갑니다. ​

 

1. x t 와 h t−1 를 concat하여 각 게이트의 선형 결합 W f x t ,W i x t ,W c x t ,W o x t 를 구합니다. ​

2. 각 게이트에 sigmoid 또는 tanh를 적용해  f t ,i t , C ~ t ,o t 를 얻습니다. ​ ​

3. 이전 셀 상태 C t−1 를 가정 값으로 두고,

C t =f t ⊙C t−1 +i t ⊙ C ~ t

h t =o t ⊙tanh(C t ) 를 실제 숫자를 대입해 계산합니다. ​ ​

4. 마지막으로 fully-connected 층 가중치 W y 를 통해 로짓 g t =W y h t 를 만들고, softmax를 적용해 최종 확률 벡터 y ^ t 를 구함으로써 순전파를 마무리합니다. ​

 

 

이 파트 덕분에 추상적인 블록 다이어그램이 “행렬곱과 시그모이드·tanh·원소별 곱·덧셈의 조합”이라는 사실이 더 명확해지고, 코드 없이도 손으로 계산을 따라가 보며 LSTM 연산 흐름을 체감할 수 있습니다. ​ ​

 

 

 

 

 

 

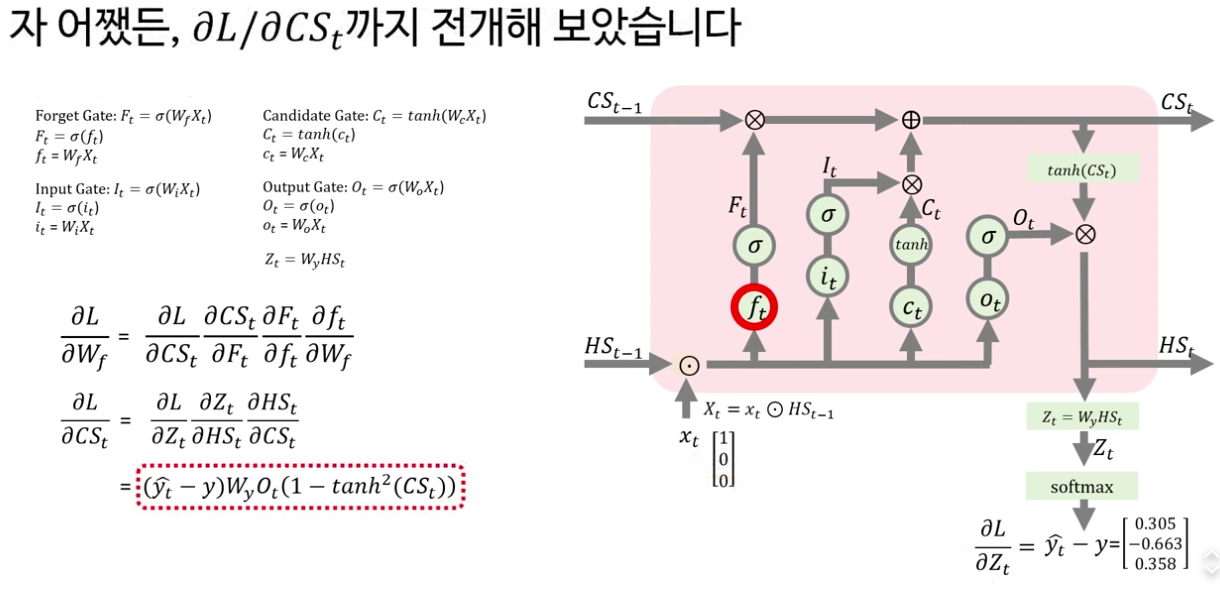
LSTM의 역전파(BPTT)와 5개 가중치의 기울기

후반부는 LSTM의 시간을 통한 역전파, 즉 BPTT를 다룹니다. 학습의 목표는 다섯 가중치 W f ,W i ,W c ,W o ,W y 각각에 대해 손실 L에 대한 기울기를 구해, 경사하강법으로 업데이트하는 것이라고 정리합니다.

 

 

 

 

· 먼저 softmax–크로스 엔트로피 조합에서 얻는 ∂L/∂g t = y ^ t −y t 를 이용해 ∂L/∂W y 를 체인 룰로 전개하고, 실제 숫자를 넣어 한 타임스텝 기준의 업데이트식을 도출합니다. ​ ​

 

 

· 이어 output 게이트의 W o 에 대한 기울기 ∂L/∂W o 를 구하기 위해, ∂L/∂h t , ∂h t /∂o t , ∂o t /∂W o 를 차례대로 계산하는 과정을 자세히 보여 줍니다. 여기서 element-wise 곱의 미분을 선형대수 관점에서 풀어 설명해, 왜 ∂h t /∂o t 에 tanh C t 만 남는지까지 짚어 줍니다. ​ ​

 

· 그 다음은 forget·input·candidate 게이트의 가중치 W f ,W i ,W c 에 대한 기울기를 비슷한 패턴으로 전개합니다. 셀 상태 공식 C t =f t ⊙C t−1 +i t ⊙ C ~ t 를 기준으로 ∂L/∂C t 를 먼저 구하고, 이를 다시 ∂L/∂f t ,∂L/∂i t ,∂L/∂ C ~ t 로 나누어 가며 각 게이트에 대한 기울기 표현을 완성합니다. ​ ​

 

 

영상에서는 시퀀스 길이를 1로 가정하고 수식을 전개하지만, 실제 다중 타임스텝에서는 RNN·LSTM에서처럼 각 시점의 기울기를 시간 방향으로 누적/전달한다는 점을 별도로 언급해, 코드 구현 시 확장 방향도 함께 안내합니다. ​ ​

 

 

 

 

 

 

 

 

 

 

LSTM이 장기 의존성을 완화하는 메커니즘

마지막 파트에서는 “왜 LSTM은 RNN보다 장기 의존성 문제가 덜 심한가?”라는 질문을, 기울기의 전달 구조를 통해 설명합니다. RNN의 경우 시간 축을 따라 1보다 작은 값들이 계속 곱해져 기울기가 급격히 0으로 수렴하는 반면, LSTM에서는 셀 상태와 은닉 상태의 기울기가 단순 곱셈만이 아니라 덧셈 형태로도 전달되기 때문에 완전히 0으로 가라앉기 어렵다는 점을 강조합니다.

 

특히 forget 게이트의 sigmoid 출력 f t 가 0~1 사이, 보통 0.5 근처의 값을 갖기 때문에, 셀 상태 변화량에 대한 기울기가 완전히 사라지지 않고 일정 수준 이상 유지될 수 있는 “안전장치” 역할을 한다고 해석합니다. 물론 LSTM도 장기 의존성 문제가 100% 사라지는 것은 아니지만, 기본 RNN과 비교하면 긴 시퀀스를 훨씬 안정적으로 학습할 수 있는 이유를 수식 구조와 함께 보여 주는 부분이 인상적입니다.

 

영상의 끝에서 강의자는 LSTM이 1990년대 제안된 이후, 트랜스포머 같은 더 강력한 모델이 등장했지만 여전히 중요한 역사적·이론적 토대라는 점을 언급하며, 다음 영상에서의 LSTM 구현 강의로 자연스럽게 이어지는 학습 경로를 제안합니다. LSTM을 처음부터 끝까지 “왜 이렇게 설계됐는지” 이해하고 싶은 학습자라면, 이 강의를 본 뒤 개념·수식 흐름을 정리해 두고 RNN·트랜스포머로 이어가는 학습 루트에 활용하기에 적합한 콘텐츠입니다.

 

 

 

[AI 인공지능 머신러닝 딥러닝/딥러닝] - 딥러닝 101 - 7강. Cross Entropy 크로스엔트로피 손실함수를 알아보자 | Deep Learning 101

딥러닝 101 - 7강. Cross Entropy 크로스엔트로피 손실함수를 알아보자 | Deep Learning 101