혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 2강

혁펜하임의 “탄탄한” 컨벡스 최적화는 머신러닝·딥러닝을 공부하는 사람들이 ‘최적화’를 진짜 수학적으로, 그러면서도 직관적으로 이해하도록 도와주는 한국어 강의 시리즈입니다.​​ 강의의 전체 구성, 수강 난이도, 어떤 수학/ML 배경이 연결되는지, 그리고 어떻게 활용하면 좋은지는 아래의 포스팅에 정리되어 있습니다.

 

[AI 인공지능 머신러닝 딥러닝] - 혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 강의 소개

혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 강의 소개

 

혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 강의

 

 

[최적화] 2-1강. 컨벡스 문제가 뭐야?

“컨벡스 최적화 문제”를 처음 정의하고 직관을 잡아 주는 강의입니다.​

1–2강에서 정리한 극대·극소와 feasible set 개념 위에, 이제 “어떤 문제가 컨벡스 문제인가?”를 공식적인 정의와 그림으로 설명하는 단계라고 보면 됩니다.​​

 

 

컨벡스 집합(convex set) 복습

강의 초반부에서는 먼저 컨벡스 집합의 정의를 다시 짚습니다.​

집합 안의 두 점 x 1 ,x 2 를 잡았을 때, 이 둘을 잇는 선분 위의 모든 점 αx 1 +(1−α)x 2 (0과 1 사이의 α)가 모두 집합 안에 포함되면 그 집합을 컨벡스라고 부른다는 조건을 그림으로 강조합니다.​

 

 

컨벡스 함수(convex function) 직관

이어서 컨벡스 함수의 정의를, “두 점에서의 함수값을 직선으로 이었을 때, 함수 그래프가 그 직선 아래에 위치하는 함수”라는 그림으로 설명합니다.​

1변수 함수에서는 이게 곡선이 ‘위로 볼록한’ 모양과 연결되고, 다변수 함수에서는 2차형식과 헤시안이 양의 준정부호인지로 판별하는 방식과도 연결된다는 점을 언급합니다.​

 

 

컨벡스 최적화 문제의 형식

그다음 이 강의의 핵심인 “컨벡스 최적화 문제”를 다음과 같은 구조로 정리합니다.​

- 목적함수 f 0 ( x ) f 0 (x)가 컨벡스 함수

- 부등식 제약 f i ( x ) ≤ 0 f i (x)≤0 들이 컨벡스 함수로 주어짐

- 등식 제약은 아핀(선형+상수) 형태로 주어짐

 

이때 이 제약들을 모두 만족하는 해들의 집합이 feasible set이 되고, 이 feasible set 자체가 컨벡스 집합이기 때문에 “컨벡스 최적화 문제”라고 부를 수 있다고 설명합니다.​

 

 

 

 

 

왜 컨벡스 문제가 중요한지 (Local = Global)

강의 후반부에서는 “왜 굳이 컨벡스 문제에 집착하느냐?”에 대한 1차 답을 줍니다.​​

컨벡스 문제에서는 local minimum이 곧 global minimum이 되기 때문에, 어떤 로컬 해만 찾아도 그게 전역 최적해라는 강력한 성질을 갖고 있고, 이 덕분에 알고리즘 설계와 이론 분석이 훨씬 쉬워진다는 점을 강조합니다.​​

 

이어서 보게 될 내용과 연결

2-1강까지 보면 “컨벡스 집합·함수·문제”라는 세 가지 축이 한 번에 연결되고, 2-2강에서는 바로 “컨벡스에 집착하는 진짜 이유: local=min global 증명”으로 넘어가게 됩니다.​​

즉 2-1강은 이후 KKT 조건, 듀얼 문제, 알고리즘들을 모두 컨벡스 프레임 안에서 다루기 위한 언어적·형식적 기반을 다지는 파트라고 볼 수 있습니다.​​

 

 

 

 

[최적화] 2-2강. 컨벡스에 집착하는 진짜 이유

이 영상은 혁펜하임 “탄탄한 컨벡스 최적화” 2-2강으로, “컨벡스면 왜 local minimum = global minimum 이 되는가?”를 정식으로 증명해 주는 내용입니다.​

 2-1강에서 컨벡스 최적화 문제를 정의했다면, 2-2강은 그 정의가 왜 그렇게 강력한지, 특히 “로컬에서만 좋아 보여도 곧 전역 최적해”가 되는 핵심 성질을 수학적으로 보여주는 강의입니다.​​ 

 

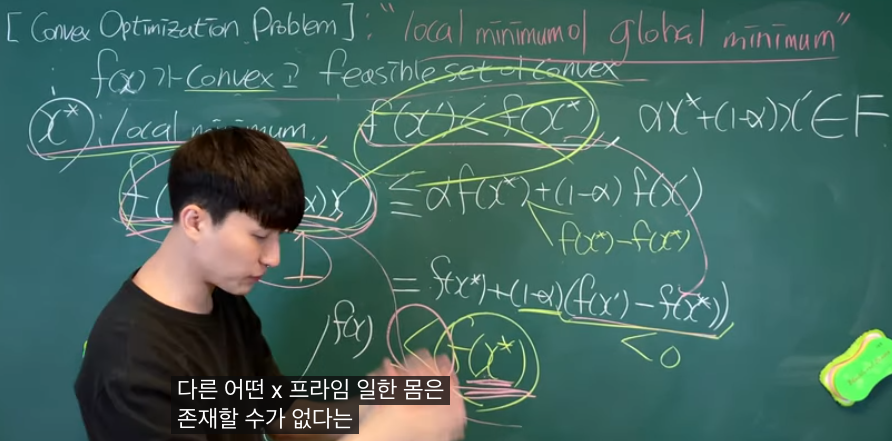
핵심 명제: Local = Global 

강의의 중심 명제는 다음과 같습니다.​ 

- 컨벡스 최적화 문제에서

-- 목적함수 f가 컨벡스이고

-- feasible set이 컨벡스 집합이면

- 어떤 점 x \* 가 feasible solution 중 하나이면서 local minimum이라면, 그 x \* 는 곧 global minimum이다.

 

즉, “로컬 미니멈에 빠졌다가 못 나오는 함정”이 컨벡스 세계에서는 사라진다는 사실을, 정의를 이용해서 직접 증명합니다.​

 

증명 아이디어 (모순법)

증명은 고전적인 모순법 구조를 따릅니다.​

 

1. x \* 가 feasible set 안의 local minimum이라고 가정

2. 그런데도 (x ′ )<f(x \* )인 다른 feasible point x ′ 가 있다고 가정

3. feasible set이 컨벡스이므로, 선분 αx \* +(1−α)x ′ (0과 1 사이 α)도 전부 feasible set 안에 들어감

4. 목적함수 f가 컨벡스이므로, 이 선분 위에서 함수값이 직선 보간보다 작거나 같은 형태의 부등식을 만족

5. 적당히 x \* 에 매우 가까운 점을 잡으면, x \* 주변에서 f 값이 f(x \* )보다 더 작아지는 점이 생김

6. 이는 “ x \* 가 주변에서 제일 작다”는 local minimum 정의와 모순

 

따라서 “더 좋은 x ′ x ′ ”가 존재한다는 가정이 틀렸고, x \* 는 global minimum일 수밖에 없다고 결론을 내립니다.​

 

왜 feasible set의 컨벡스성이 필요할까

강의 중간에서는 “왜 하필 feasible set까지 컨벡스여야 하냐”를 따로 짚습니다.​

- 위 증명에서 “선분을 따라가도 항상 feasible”이라는 사실이 꼭 필요

- feasible set이 컨벡스가 아니면, x \* 와 x ′ 사이 선분 중간에 있는 점들이 제약을 위반할 수 있고, 그 점들에서는 “local minimum”을 논할 자격 자체가 없어짐

 

즉, “local minimum은 feasible solution들 중에서만 정의된다”는 점을 강조하면서, 컨벡스 문제 정의에 왜 ‘컨벡스 집합’이 같이 들어가는지도 자연스럽게 설명합니다.​

 

 

컨벡스 최적화에서 이 성질의 의미

이 명제가 중요한 이유는, 컨벡스 최적화에서는 “어떤 로컬 해만 찾아도 그게 곧 전역 최적해”라는 강력한 보증을 주기 때문입니다.​

그래서 경사하강법 등 비교적 단순한 알고리즘으로도 잘 설계된 컨벡스 문제에서는 “수렴만 하면 곧 글로벌 솔루션”이라는 안심을 할 수 있고, 이 점이 비컨벡스 딥러닝과 대비되는 가장 큰 차이점 중 하나로 등장합니다.​

 

 

 

 

[AI 인공지능 머신러닝 딥러닝] - 혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 3강

혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 3강