혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 3강

혁펜하임의 “탄탄한” 컨벡스 최적화는 머신러닝·딥러닝을 공부하는 사람들이 ‘최적화’를 진짜 수학적으로, 그러면서도 직관적으로 이해하도록 도와주는 한국어 강의 시리즈입니다.​​ 강의의 전체 구성, 수강 난이도, 어떤 수학/ML 배경이 연결되는지, 그리고 어떻게 활용하면 좋은지는 아래의 포스팅에 정리되어 있습니다.

 

[AI 인공지능 머신러닝 딥러닝] - 혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 강의 소개

혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 강의 소개

 

혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 강의

 

 

[최적화] 3-1강. 경사하강법 (Gradient Descent) 미분만 알면 돼!

이 영상은 혁펜하임 “탄탄한 컨벡스 최적화” 3-1강으로, 제약이 없는(unconstrained) 최적화에서 가장 기본이 되는 알고리즘인 경사하강법(Gradient Descent)을 직관과 예제로 설명하는 강의입니다.​

딥러닝에서 손실 함수를 줄이는 업데이트 공식 x k + 1 = x k − α ∇ f ( x k ) x k+1 =x k −α∇f(x k )가 어디서 나오는지, 미분·기울기 관점에서 차근차근 연결해 주는 내용입니다.​

 

 

경사하강법이 하는 일

경사하강법은 “함수 값을 줄이는 방향으로 조금씩 움직이면서 최소값에 가까이 가는 반복 알고리즘”입니다.​

초기값 x 0 x 0 를 정한 뒤, 그 지점에서의 gradient(기울기)를 계산하고, 함수가 가장 빠르게 감소하는 방향인 − ∇ f ( x ) −∇f(x) 쪽으로 조금 이동하는 과정을 반복해서 로컬 혹은 글로벌 최소점을 찾습니다.​

 

 

알고리즘 업데이트 공식

강의에서 정리하는 경사하강법의 핵심 업데이트 규칙은 다음과 같습니다.​

x k + 1 = x k − α ∇ f ( x k ) x k+1 =x k −α∇f(x k )

 

- ∇f(x k ): 현재 위치에서의 가장 가파른 상승 방향

- −∇f(x k ): 가장 가파른 하강 방향

- α: step size, learning rate에 해당하는 하이퍼파라미터

 

이 공식을 반복하면서 함수 값이 줄어드는 방향으로 점들을 이동시키고, gradient가 0에 가까워지면 멈추는 식으로 구현합니다.​

 

 

 

step size(학습률)의 역할

영상에서는 step size를 너무 크게 잡으면 최소점을 지나쳐 발산하고, 너무 작게 잡으면 수렴은 하지만 “아주 느린 내려가기”만 반복된다는 점을 그림과 함께 강조합니다.​

실제로 적당한 α를 잡으면, gradient의 크기 자체가 점점 작아지기 때문에 자연스럽게 이동량도 줄어들며 최소점 근처에서 안정적으로 멈추게 된다는 직관을 설명합니다.​

 

 

 

1차원·다차원 직관

1차원 예시에서는 “기울기 부호로 왼쪽/오른쪽 어디로 가야 내려가는지”를 보는 식으로, 경사하강법을 고등학교 수준 함수 그래프에 연결해 줍니다.​

다차원에서는 gradient 벡터가 “각 좌표 방향으로 얼마나, 어느 쪽으로 변화해야 함수를 가장 빨리 줄일 수 있는지”를 알려주는 방향 벡터라는 점을 설명하며, 벡터/행렬 표기( ∇ f ( x ) ∇f(x), transpose 등)로 일반화합니다.​

 

 

 

예시: 선형 모델 + 제곱 오차

후반부에는 “머릿속의 진짜 파라미터를 노이즈 섞인 관측으로 추정한다”는 설정으로, 선형 모델에 제곱 오차(cost)를 두고 경사하강법을 적용하는 예제를 풉니다.​

이 과정에서 에러 함수가 항상 스칼라여야 하는 이유, 벡터·행렬 곱을 transpose로 정리하는 법, 그리고 실제로 gradient를 구해 업데이트 식을 구현하는 흐름까지 보여 주어, 딥러닝에서 파라미터 업데이트가 어떻게 동일한 틀로 돌아가는지를 연결해 줍니다.​

 

 

 

 

 

[최적화] 3-2강. 뉴턴법 (Newton's method) 쉬운 설명

이 영상은 혁펜하임 “탄탄한 컨벡스 최적화” 3-2강으로, 뉴턴법(Newton’s method)을 “방정식의 근 찾기 → 최적화”로 자연스럽게 연결해서 설명하는 강의입니다.​ 

3-1강의 경사하강법이 1차 미분(gradient)만 쓰는 방법이라면, 3-2강의 뉴턴법은 2차 미분(헤시안, Hessian)까지 써서 더 빠르게 최소점을 찾는 2계 방법(second-order method)입니다.​ 

 

 

뉴턴법의 기본 아이디어 

원래 뉴턴법은 f ( x ) = 0 f(x)=0 형태의 방정식에서 “해가 있는 x를 찾는 제로 파인딩 알고리즘”입니다.​ 현재 점에서의 접선(1차 테일러 근사)을 이용해 함수 그래프를 직선으로 근사하고, 그 직선이 x축과 만나는 점으로 이동하는 과정을 반복하면서 0이 되는 지점에 빠르게 근접합니다.​ 

 

 

 

제로 파인딩 → 최적화로 옮기기

최소점을 찾는다는 것은 “gradient가 0이 되는 점”을 찾는 것과 같습니다.​ 

그래서 뉴턴법을 f ( x ) f(x)가 아니라 ∇ f ( x ) ∇f(x)에 적용하면, ∇ f ( x ) = 0 ∇f(x)=0을 만족하는 지점(정지점)을 찾는 알고리즘이 되고, 이것이 최적화에서의 뉴턴법입니다.​ 

 

뉴턴 업데이트는 다음과 같은 꼴이 됩니다.​ 

x k + 1 = x k − H f ( x k ) − 1 ∇ f ( x k ) x k+1 =x k −H f (x k ) −1 ∇f(x k ) 

여기서 

- ∇f(x k ): gradient (1차 미분)

- H f (x k ): Hessian (2차 미분을 모아 만든 행렬) 입니다.

 

 

 

경사하강법과의 차이

경사하강법은 x k + 1 = x k − α ∇ f ( x k ) x k+1 =x k −α∇f(x k )처럼 gradient 방향만 보고 고정된 step size α α를 곱해 내려갑니다.​

반면 뉴턴법은 헤시안의 역행렬 H − 1 H −1 로 gradient를 “곡률에 맞게 스케일링”해서, 일종의 자동 step size + 방향 조정을 동시에 해 주기 때문에 최소점 근처에서 매우 빠른(이론적으로는 이차 수렴) 수렴 속도를 가집니다.​

 

 

 

2차 근사와 이차 수렴 직관

강의에서는 테일러 전개로 함수 f ( x ) f(x)를 2차식으로 근사한 뒤, 그 2차식의 최소점을 한 번에 푸는 과정에서 뉴턴 스텝이 자연스럽게 도출된다는 점을 보여 줍니다.​

특히 목적 함수가 진짜 2차함수(예: 최소제곱 문제)인 경우, 뉴턴법 업데이트는 일반적인 선형 least squares 정규방정식과 동일해져서 “한 번에 해를 찾아버리는” 현상이 나타난다는 점도 예제로 강조합니다.​

 

 

 

장점과 한계

- 장점: 최소점 근처에서 매우 빠른 수렴(이차 수렴), step size를 따로 튜닝하지 않아도 되는 구조, 2차 근사 기반의 ‘똑똑한’ 이동.​

- 한계: 헤시안 계산·역행렬 계산 비용이 크고, 비볼록 문제나 시작점이 좋지 않은 경우에는 발산하거나 saddle point로 갈 수 있다는 점 때문에, 실제 대규모 딥러닝에서는 변형된 quasi-Newton, L-BFGS류가 더 자주 사용됩니다.​

 

강의 후반부에서는 경사하강법, 뉴턴법, 그리고 2차 least squares 해법을 나란히 두고 “느리지만 단순한 1계 방법 vs 빠르지만 무거운 2계 방법”이라는 대비로 정리해, 이후 다른 최적화 알고리즘(가우스–뉴턴, quasi-Newton 등)을 이해할 수 있는 발판을 마련해 줍니다.​

 

 

 

[최적화] 3-3강. 가우스-뉴턴법 (Gauss-Newton method) 일반식 유도

이 영상은 혁펜하임 “탄탄한 컨벡스 최적화” 3-3강으로, 비선형 최소제곱(nonlinear least squares) 문제에 대한 가우스–뉴턴(Gauss–Newton) 방법의 일반식을 유도하는 강의입니다.​ 

3-2강의 뉴턴법을 그대로 쓰기에는 2차 미분(헤시안)이 너무 부담스러운 상황에서, “1차 미분(야코비안)만 써서 뉴턴법을 흉내 내는 방법”으로 가우스–뉴턴을 소개하는 흐름입니다.​ 

 

 

문제 설정: 비선형 최소제곱 

가우스–뉴턴법은 “잔차(residual)를 제곱해서 더한 것”을 최소화하는 비선형 최소제곱 문제를 대상으로 합니다.​ 

보통 다음과 같은 꼴로 쓰며, r ( x ) r(x)는 m m-차원 잔차 벡터, x x는 n n-차원 파라미터입니다.​

 min ⁡ x 1 2 ∥ r ( x ) ∥ 2 2 x min 2 1 ∥r(x)∥ 2 2 

 

예: 비선형 모델 y ≈ f ( x ; θ ) y≈f(x;θ)에서 관측값과 모델 출력의 차이를 모아 잔차 r ( θ ) r(θ)를 만들고, 그 제곱합을 최소화하는 문제입니다.​ 

 

 

뉴턴법을 그대로 쓰면 생기는 문제 

이 목적함수에 뉴턴법을 직접 적용하면, gradient와 Hessian을 모두 계산해야 합니다.​

 

- gradient:

∇ f ( x ) = J ( x ) ⊤ r ( x ) ∇f(x)=J(x) ⊤ r(x) (여기서 J ( x ) J(x)는 잔차 r ( x ) r(x)의 야코비안)

- Hessian:

∇ 2 f ( x ) = J ( x ) ⊤ J ( x ) + ∑ i r i ( x ) ∇ 2 r i ( x ) ∇ 2 f(x)=J(x) ⊤ J(x)+∑ i r i (x)∇ 2 r i (x) 형태로, 각 잔차의 2차 미분까지 필요해 계산과 구현이 매우 복잡해집니다.​

 

강의에서는 이 “Hessian 계산 부담”이 가우스–뉴턴이 등장하는 출발점이라는 점을 강조합니다.​

 

 

 

가우스–뉴턴 아이디어: Hessian 근사

가우스–뉴턴법은 위의 Hessian에서 “잔차에 곱해진 2차 미분 항”을 버리고, J ( x ) ⊤ J ( x ) J(x) ⊤ J(x)만 남기는 근사를 사용합니다.​

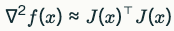
∇ 2 f ( x ) ≈ J ( x ) ⊤ J ( x ) ∇ 2 f(x)≈J(x) ⊤ J(x)

 

이 근사는 잔차가 충분히 작거나, 목적함수가 최소점 근처에서 거의 이차함수처럼 보일 때 특히 잘 맞습니다.​

이렇게 하면 2계 미분 없이도, 1계 미분(야코비안)만으로 “뉴턴에 가까운” 업데이트를 만들 수 있습니다.​

 

 

가우스–뉴턴 업데이트 일반식

뉴턴법 업데이트

x k + 1 = x k − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) x k+1 =x k −[∇ 2 f(x k )] −1 ∇f(x k )

에 위 근사를 대입하면, 다음과 같은 가우스–뉴턴 스텝이 나옵니다.​

 

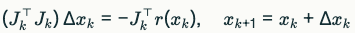
( J k ⊤ J k ) Δ x k = − J k ⊤ r ( x k ) , x k + 1 = x k + Δ x k (J k ⊤ J k )Δx k =−J k ⊤ r(x k ),x k+1 =x k +Δx k

여기서 J k = J ( x k ) J k =J(x k )입니다.​

 

즉, 매 반복마다

- 잔차를 1차로 선형화하고

- 그 선형근사에 대한 “선형 최소제곱 문제”를 푼 결과를 Δ x k Δx k 로 사용해 파라미터를 업데이트하는 방식입니다.​

 

 

직관과 활용 포인트

강의에서는 “매 step마다 비선형 문제를 ‘근처에서 선형 문제’로 바꾸고, 그 선형 least squares 해를 이용해 한 번 더 점프하는 과정”이라는 직관으로 정리합니다.​

뉴턴법보다 계산은 가벼우면서, 단순 gradient descent보다는 빠르고 구조를 잘 활용하는 방법이라, 비선형 곡선피팅, 파라미터 추정, 컴퓨터 비전·신호처리 등에서 널리 쓰이는 기법이라는 점도 함께 다룹니다.

 

 

 

 

[AI 인공지능 머신러닝 딥러닝] - 혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 4강

혁펜하임의 “탄탄한” 컨벡스 최적화 (Convex Optimization) 4강