이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 6강 시그모이드, 로지스틱 회귀, MSE, 소프트맥스
[AI 인공지능 머신러닝 딥러닝] - 이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 - 무료 강의 및 책 소개
이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 - 무료 강의 및 책 소개
한국어로 딥러닝 공부해봤다는 사람중에 안들어 본 사람이 없을것 같은 이지 딥러닝 시리즈 입니다. 이 강의는 유투브로 제공되며 책도 있습니다. 이지 딥러닝 유투브 강의이지 딥러닝 유투브
inner-game.tistory.com
[Easy! 딥러닝] 6-1강. 왜 이진 분류에서 sigmoid를 사용할까? (강의 통틀어 가장 어려운 부분)
이 강의의 핵심은 “유닛 스텝 함수로도 이진 분류는 가능한데, 너무 빡빡하고 미분이 안 되기 때문에, 이를 부드럽게 만든 시그모이드(sigmoid)를 사용해서 ‘확률’과 ‘정도의 차이’를 표현하며 학습까지 가능하게 만든다”입니다.
퍼셉트론과 유닛 스텝 함수
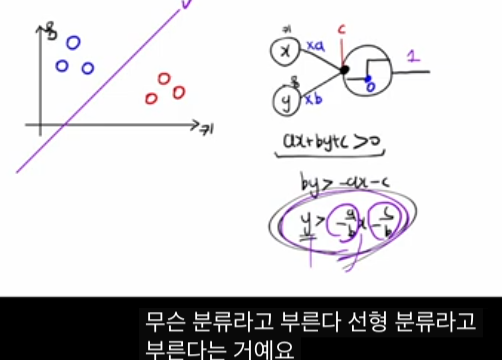
이 강의는 키·몸무게로 “지금 당장 살을 빼야 할 사람(1) vs 살을 더 찌워야 할 사람(0)”을 분류하는 이진 분류 예제로 시작합니다. 히든 레이어 없이 입력 두 개(키, 몸무게)와 출력 하나만 있는 가장 단순한 신경망에 유닛 스텝 함수(unit step function)를 activation으로 쓰면, 이것이 바로 고전적인 퍼셉트론(perceptron)입니다.
- 퍼셉트론의 출력은 z=ax+by+c 을 계산한 뒤, 0 z>0이면 1, z≤0이면 0을 내보내는 구조입니다.
- 이때 ax+by+c=0인 직선이 “분류 경계선(decision boundary)”가 되고, 이 선 위쪽은 1, 아래쪽은 0으로 나뉘기 때문에 “선형 분류(linear classification)”라고 부릅니다.
입력–출력의 관계 그래프는 계단처럼 0과 1 사이를 갑자기 점프하는 비선형 형태지만, 경계선 자체가 직선이기 때문에 선형 분류로 분류한다는 점을 강조합니다.


유닛 스텝 함수의 두 가지 문제
유닛 스텝 함수만으로 이진 분류를 하면 다음과 같은 문제가 생깁니다.
1. 미분 불가능 → 그라디언트 디센트 불가
- 스텝 함수는 경계 지점에서 갑자기 값이 튀기 때문에 도함수(기울기)가 정의되지 않습니다.
- 그래서 딥러닝에서 사용하는 그라디언트 디센트 기반 학습(역전파)을 쓸 수 없고, 고전적 퍼셉트론 룰 같은 별도의 업데이트 규칙이 필요합니다.
2. 분류가 너무 “빡빡함” (0/1밖에 없음)
- 경계선 바로 아래에 있어도 0, 바로 위에 있어도 1이라서, “얼마나 빼야/얼마나 찌워야 하는지” 정도를 표현할 수 없습니다.
- 데이터가 극단적인 경우(진짜로 심각하게 빼야 할 사람 vs 진짜로 심각하게 찌워야 할 사람)인데도, 경계선이 둘 사이에 너무 가깝게 서 있어도 스텝 함수만 보면 둘 다 “정답 100점”인 경계선이라 구분이 안 됩니다.
이 두 가지 한계를 해결하기 위해 “유닛 스텝을 부드럽게 펼친” 시그모이드 함수가 등장합니다.

시그모이드 함수의 모양과 성질
시그모이드(sigmoid)는 아래와 같은 S자 형태의 함수로, 모든 실수 입력을 0과 1 사이의 값으로 압축합니다.


- x=0이면 σ(0)=0.5라서 분류의 자연스러운 기준값(임계값)으로 쓰기 좋습니다.
- x→+∞면 1에, x→−∞면 0에 점점 가까워지기 때문에 유닛 스텝과 비슷한 모양이지만, 중간이 매끄럽게 이어지는 것이 특징입니다.
그래서 시그모이드는:
- 전 구간에서 미분 가능 → 그라디언트 디센트를 이용한 학습이 가능해짐
- 출력이 0~1 사이의 연속 값 → “확률”이나 “정도”로 해석 가능
이라는 장점을 동시에 가집니다.
왜 이진 분류에 시그모이드를 쓰는가?
영상의 논리는 “스텝의 단점을 시그모이드가 한 번에 해결한다”로 정리됩니다.
1. 부드러운 분류(soft classification)
- 경계선 근처의 점도 0.5±ε 식으로 조금씩 다른 값을 내므로, “조금만 빼면 됨(예: 0.55)”, “엄청 많이 빼야 함(예: 0.95)”처럼 강도를 숫자로 표현할 수 있습니다.
- 3D로 보면, 스텝 함수일 때는 경계선을 기준으로 0과 1이 평평하게 잘려 있는 계단 모양이지만, 시그모이드는 경계선 주변에서 완만한 언덕/비탈 형태로 이어집니다.
2. 가장 “합리적인” 경계선을 찾아줌
- 스텝 함수만 쓰면, 극단적인 두 집단 사이에 여러 개의 선형 경계선이 모두 “정답 100점”이어서 어떤 게 좋은지 구별할 수 없습니다.
- 시그모이드를 쓰면, 각 점에서 “1에 얼마나 가깝게, 0에 얼마나 가깝게” 출력되는지가 손실 함수에 반영되어, 양측 극단과 멀리 떨어진 여유 있는 경계선이 더 높은 점수를 받게 됩니다.
3. 확률로 해석 가능
- 출력을 “이 사람이 1번 클래스(예: 빼야 하는 사람)일 확률”로 해석할 수 있습니다.
- 예를 들어 0.9면 “1 클래스일 확률 90%”, 0.1이면 “10%”처럼 직관적 확률 해석이 가능하고, 0.5를 기준으로 0/1로 컷팅할 수도 있습니다.
이 때문에, 딥러닝에서 이진 분류의 출력층 activation으로 시그모이드를 사용하는 것이 표준적인 선택이며, 로지스틱 회귀(logistic regression)와도 자연스럽게 연결됩니다.

이 강의에서는 키와 몸무게로 사람을 둘 중 하나의 상태로 분류하는 단순한 예제를 통해, 퍼셉트론과 유닛 스텝 함수가 어떻게 선형 결정 경계를 만들고 이진 분류를 수행하는지 직관적으로 설명합니다. 하지만 유닛 스텝 함수는 미분이 불가능해 그라디언트 기반 학습을 사용할 수 없고, 경계선 바로 위와 아래의 점도 무조건 0 또는 1로만 처리하여 분류가 지나치게 빡빡하다는 한계를 가집니다. 이를 부드럽게 보완한 시그모이드 함수는 0과 1 사이의 연속적인 값을 출력하면서 미분 가능하다는 장점을 가져, 딥러닝에서 이진 분류 문제의 출력층에 널리 사용되는 대표적인 비선형 활성화 함수입니다.

[Easy! 딥러닝] 6-2강. 로지스틱 회귀(Logistic regression)의 모든 것 | 이진 분류 (binary classification)
이 강의의 핵심은 “시그모이드 출력 q를 ‘강아지/고양이일 확률’로 해석하고, 그 확률을 최대화하는 과정을 수식으로 정리하면 바로 Binary Cross Entropy(BCE) 로스가 되고, 이 구조 전체를 로지스틱 회귀(logistic regression)라고 부른다”입니다.



BCE 로스가 나오는 직관
강아지(레이블 y=1) 사진이 들어왔을 때는 “강아지일 확률 q”를 키우고 싶고, 고양이(y=0) 사진일 때는 “고양이일 확률 1−q”를 키우고 싶습니다. 이를 한 줄로 쓰면, 각 샘플에 대해 “정답 클래스에 해당하는 확률”을 키우면 되는 것이고, 그 값은 q^y+(1−q)^(1−y)처럼 표현됩니다.

- 여러 샘플(독립 시행)에 대해 “해당 동물일 확률”을 곱해서 전체 확률을 최대화하는 것은, 통계적으로 말하면 로그 우도(log-likelihood)를 최대화하는 것입니다.
- 곱하면 언더플로우가 나기 때문에 로그를 취해 합으로 바꾸고, “최대화”를 “최소화” 관점으로 바꾸기 위해 마이너스를 붙이면

형태의 Binary Cross Entropy (BCE) 로스가 됩니다. 로그를 써도 되는 이유는 로그가 단조 증가 함수라서, “원래 확률을 키우기”와 “로그 확률을 키우기”가 같은 방향의 최적화를 의미하기 때문입니다.
로지트, 로지스틱 회귀 해석
시그모이드 출력 q를 확률이라 두고, 이를 “승산(odds)”과 “로지트(logit)”로 다시 표현할 수 있습니다.
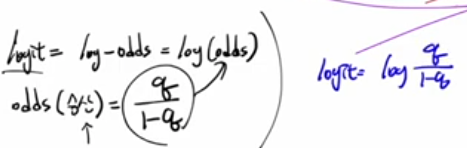
- 승산(odds):

- 로지트(logit):

이 식을 정리하면

이 되어, “로지트에 시그모이드를 씌우면 확률이 된다”는 관계가 나옵니다.

강의에서는 시그모이드 바로 직전 값을 “로지트 L”라고 보고, 이 L을 입력 x에 대한 선형 회귀식 L=w ⊤ x+b 로 모델링하면, “로지트를 선형 회귀로 구하고, 시그모이드로 확률로 변환하는” 구조가 바로 로지스틱 회귀라고 설명합니다.


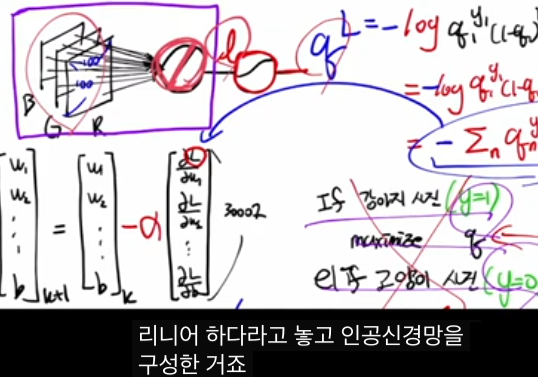
이 관점에서 보면:
- w ⊤ x+b까지는 선형 회귀(regression)
- 시그모이드는 “네트워크 내부의 액티베이션”이라기보다, 로스를 계산하기 위해 로지트를 확률로 바꾸는 링크 함수 역할로 볼 수 있습니다.
정리: 로지스틱 회귀 = “확률을 잘 맞추는 회귀”
로지스틱 회귀는 입력 x에 대해 “y=1일 확률”을 출력하는 모델이며, 내부적으로는
- 로지트 z=w ⊤ x+b를 선형으로 만들고,
- 시그모이드로 z를 0~1 확률 q로 바꾼 다음,
- BCE 로스를 최소화하도록 w,b를 학습하는 방식입니다.
즉, 이진 분류(binary classification)를 “확률을 예측하는 회귀 문제”로 바라본 것이 로지스틱 회귀이고, BCE 로스는 “정답 분포와 모델 확률 분포 사이의 차이(교차 엔트로피)”를 최소화하는 자연스러운 선택입니다.
[Easy! 딥러닝] 6-3강. MSE vs BCE 비교 분석
이 강의의 핵심은 “이진 분류에서 MSE도 쓸 수는 있지만, BCE를 쓰면 (1) 잘못된 예측에 더 민감하게 페널티를 주고, (2) 출력층 가중치에 대해 로스 함수가 convex에 가까워져 학습이 더 안정적”이라는 점입니다.


1. “강아지 1이어야 하는데 0 나왔다”에서의 민감도
강아지 사진(레이블 y=1) 한 장에 대해 예측 q 1 이 나왔다고 할 때, 두 로스는 다음처럼 정의됩니다.
- MSE: (q 1 −1) ^2
- BCE: −log(q 1 ) (이진 레이블 1이므로 −logq 1 만 남음)

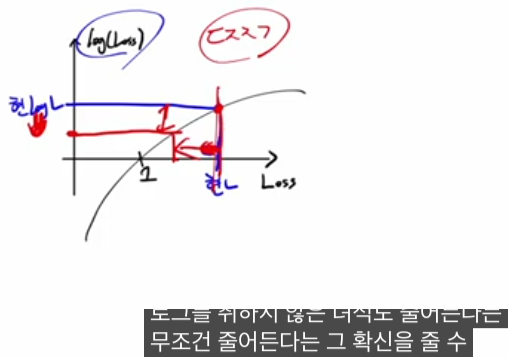
이 둘을 q 1 ∈(0,1]에서 그려보면:
- (q 1 −1) ^2 는 최대 로스가 1이고, q 1 =0일 때도 “1만큼 틀렸다”고만 평가합니다.
- −logq 1 는 q 1 →0로 갈수록 로스가 무한대로 발산하여, “1이었어야 하는데 0이라고 확신한” 최악의 경우를 훨씬 강하게 벌줍니다.
그래서 BCE는:
- 살짝 틀린 예측에는 적당한 페널티,
- 완전히 반대로 확신한 예측에는 매우 큰 페널티
를 주기 때문에, 이진 분류 문제에서 확률값의 차이를 더 섬세하게 반영합니다.
2. 출력층에서의 convex 구조
출력층의 가중치 하나 w만 남기고 나머지 가중치를 0, 그에 곱해지는 입력을 1이라고 단순화하면, 시그모이드 출력 q(w)는 w에 대한 단조 증가 함수가 됩니다.


이때 로스를 w에 대한 함수로 보면:
- BCE 로스 L BCE (w)는 w에 대해 아래로 볼록한(convex) 모양이 됩니다.
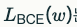
-- convex라서 출발점이 어디든, 적당한 러닝레이트만 쓰면 전역 최솟값으로 수렴합니다.
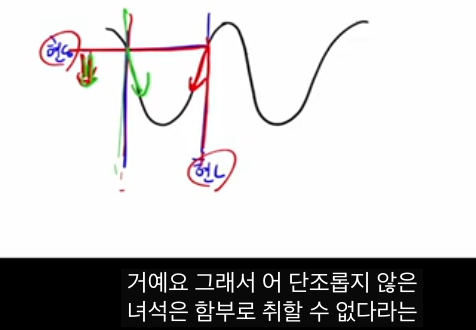
- 같은 설정에서 MSE 로스 L MSE (w)는 시그모이드와 제곱이 섞이면서 non-convex 모양이 되어, 로컬 미니마에 빠질 가능성이 있습니다.

실제 딥 네트워크(히든 레이어가 있는 경우)는 어차피 전체적으로 non-convex지만,
- BCE를 쓰면 최소한 출력층 가중치에 대해서는 보다 예쁜(convex에 가까운) 로스 지형을 얻고,
- MSE를 쓰면 출력층부터 이미 더 “울퉁불퉁한” non-convex를 가지므로, 더 깊은 층에서는 그 왜곡이 더 커질 수 있다는 직관을 줍니다.
이 강의에서는 “이진 분류에서 시그모이드를 쓴다면 MSE 대신 BCE를 사용하는 것이 왜 더 자연스러운지”를 두 가지 관점에서 비교합니다. 첫째, 강아지·고양이처럼 0과 1로 나뉘는 문제에서, MSE는 최악의 예측에도 로스를 1까지만 줄 수 있는 반면, BCE는 잘못된 확신에 대해 로스를 무한대까지 키울 수 있어 잘못된 분류에 훨씬 민감하게 반응합니다. 둘째, 출력층 가중치에 대해 로스 함수를 단순화해 살펴보면, BCE 로스는 아래로 볼록한 형태를 가져 전역 최솟값으로 수렴하기 쉬운 반면, MSE는 non-convex 구조를 만들어 로컬 최솟값에 빠질 위험이 더 크다는 점에서, 이진 분류에서는 BCE가 더 안정적이고 이론적으로도 잘 정당화된 선택입니다.
[Easy! 딥러닝] 6-4강. 이거 많이 어렵습니다.. 상위 1%만 알고 있는 딥러닝의 뿌리 이론! MLE (Maximum Likelihood Estimation)
이 강의의 핵심은 “딥러닝에서 쓰는 대표적인 손실 함수(MSE, BCE 등)는 그냥 감으로 만든 것이 아니라, 확률 모델을 세우고 최대우도추정(MLE)을 적용하면 자연스럽게 유도된다”는 것입니다.



딥러닝 = 확률모델 + MLE
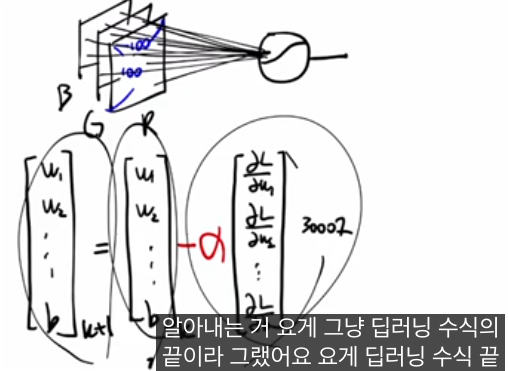
강의에서는 먼저 딥러닝을 “입력 x가 들어왔을 때 정답 y가 나올 확률 p θ (y∣x)를 모델링하는 확률모델”로 봅니다. 여기서 θ는 신경망의 모든 가중치·바이어스를 모은 파라미터이고, 학습이란 “실제 관측된 데이터들이 최대한 그럴듯하게 나오도록 θ를 고르는 과정”입니다.
- MLE(Maximum Likelihood Estimation)의 목표는

즉, 모든 데이터가 동시에 관측될 가능도(likelihood)를 최대화하는 θ를 찾는 것입니다.
- 계산 편의를 위해 로그를 취해 로그우도(log-likelihood) 합으로 바꾸고, 부호를 바꿔 “손실(loss)” 형태로 쓰면

이 됩니다.
딥러닝이 하는 일은 결국 “어떤 분포를 가정하느냐에 따라 정의된 이 손실 L을 최소화하는 θ를 찾는 것”이라는 뿌리를 보여줍니다.
MSE와 BCE가 MLE에서 어떻게 나온다고 보는가
강의 전까지 배운 MSE, BCE를 “확률분포 가정 + MLE” 관점에서 재해석합니다.
- 회귀 + MSE:
출력 y가 “모델 예측 y^햇 θ (x)를 평균으로 하는 가우시안(정규분포)”라고 가정하고, 분산은 상수로 두면, 그 분포의 음의 로그우도를 전개했을 때 MSE와 비례하는 손실이 나옵니다.
그래서 회귀에서 MSE를 쓰는 것은 “정규분포 오차 가정 하에서 MLE를 한 것”과 동치입니다.
- 이진 분류 + BCE:
레이블 y∈{0,1}를 베르누이(Bernoulli) 분포

로 보고, 여기에 MLE를 적용하면 음의 로그우도가
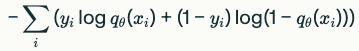
가 되어, 바로 BCE(Binary Cross Entropy) 로스가 됩니다.
즉 “왜 굳이 이런 수식을 쓰냐?”에 대한 대답이 “MLE 관점에서 가장 자연스럽기 때문”이라는 점을 강조합니다.




log, NLL, Cross-Entropy, KL과의 연결
강의에서처럼, 로그를 취해 “곱 → 합”으로 바꾸고 부호를 바꿔 손실로 쓰면, 이건 통계에서 말하는 음의 로그우도(Negative Log-Likelihood, NLL)입니다. NLL을 평균 내서 쓰면, 정보이론에서의 교차 엔트로피(cross-entropy)와 형태가 같아지고, 이는 “데이터의 실제 분포와 모델 분포 사이의 KL 발산을 최소화하는 것”과도 연결됩니다.
- MLE ↔ NLL 최소화 ↔ 교차 엔트로피 최소화 ↔ KL 발산 최소화(상수 항 제외)라는 연결 고리를 통해, “딥러닝 학습 = 데이터 분포와 모델 분포를 가깝게 만드는 과정”이라는 큰 그림을 보여주는 것이 이 강의의 포인트입니다.

이 강의에서는 딥러닝에서 사용하는 대표적인 손실 함수들이 모두 확률론적 뿌리를 가지고 있으며, 최대우도추정(MLE)이라는 공통 원리에서 자연스럽게 유도된다는 점을 설명합니다. 회귀 문제에서 MSE는 출력이 정규분포를 따른다고 가정하고 그 음의 로그우도(Negative Log-Likelihood)를 최소화한 결과이고, 이진 분류에서 BCE는 레이블을 베르누이 분포로 보고 MLE를 적용했을 때 얻어지는 로그우도 손실입니다. 더 나아가 로그우도에 마이너스를 붙인 손실은 교차 엔트로피와 KL 발산과도 연결되어, 딥러닝 학습 전체를 “데이터의 실제 분포와 모델이 만드는 확률 분포를 최대한 가깝게 만드는 과정”으로 해석할 수 있다는 점에서, MLE는 딥러닝 이론의 중요한 뿌리 개념이라고 할 수 있습니다.

[Easy! 딥러닝] 6-5강. 소프트맥스 회귀(Softmax regression)의 모든 것 | 다중 분류 (multiclass classification)
이 강의의 핵심은 “다중 분류에서는 출력층을 소프트맥스(softmax)로 확률 분포로 만들고, 멀티클래스 크로스 엔트로피(categorical cross-entropy) 로스를 최소화하는 것이 곧 소프트맥스 회귀(= 멀티노미얼 로지스틱 회귀)”라는 점입니다.


다중 분류 세팅과 원-핫 레이블
강의에서는 3×100×100 RGB 이미지가 들어오고, 강아지/고양이/소 세 클래스 중 하나로 분류하는 예시로 시작합니다.
출력층에 노드 3개를 두고 각 노드가 “강아지일 확률, 고양이일 확률, 소일 확률”을 담당하게 만들기 위해, 레이블을 one-hot 벡터 (1,0,0),(0,1,0),(0,0,1) 형태로 약속합니다.

이때 목표는 “입력 x i 가 들어가면 출력 q i =(q i1 ,q i2 ,q i3 )가 정답 레이블 y i =(y i1 ,y i2 ,y i3 )와 최대한 비슷해지도록 하는 것”이며, 이 분포 간 차이를 재는 손실로 크로스 엔트로피를 씁니다.
소프트맥스 함수와 그 역할
출력층 선형결과(로짓) L=(L 1 ,L 2 ,L 3 )에 대해 소프트맥스는

로 정의되어, 모든 q k 가 양수이고 합이 1인 확률 분포가 됩니다.
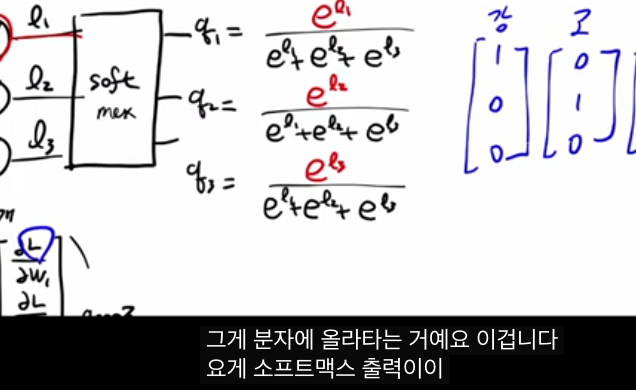


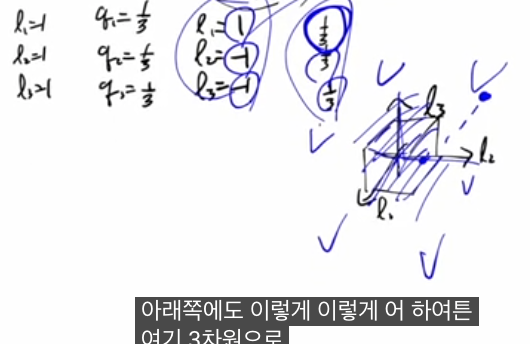

지수와 정규화를 쓰기 때문에 값의 크기 차이를 잘 반영하면서도, 각 클래스별 “신뢰도”를 해석 가능한 확률로 바꿔 줍니다.
절댓값으로 나눠 정규화하거나 각 노드에 개별 시그모이드를 쓰는 방식도 생각할 수 있지만,
- 절댓값 정규화는 부호 정보를 잃어 좌표 공간 일부만 실질적으로 쓰게 되고,
- 개별 시그모이드는 합이 1이 아니어서 “이 중 반드시 하나”라는 경쟁 구조가 약해져 멀티클래스(one-of-K)보다는 멀티레이블(여러 개 동시에 참) 문제에 더 적합하다는 점을 영상에서 비교합니다.
멀티클래스 크로스 엔트로피와 MLE
다중 분류에서는 레이블이 멀티노미얼(카테고리컬) 분포를 따른다고 가정하고, 그에 대한 최대우도추정(MLE)을 하면 소프트맥스 + 크로스 엔트로피 구조가 자연스럽게 나옵니다.






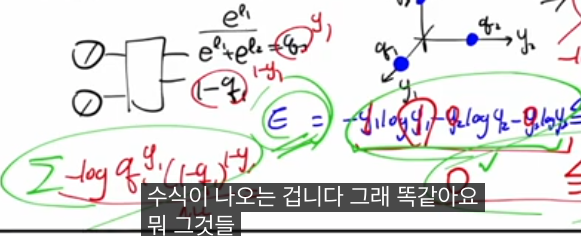
- 소프트맥스로 얻은 q=(q 1 ,…,q K )와 one-hot 레이블 y에 대해, 한 샘플의 크로스 엔트로피는

이고, one-hot이면 정답 클래스 k \* 에 대해서만 −logq k \* 가 남습니다.
- 여러 샘플에 대해 이 값을 합(또는 평균)한 것이 손실이며, 이것을 줄이면 모델 분포 q가 레이블 분포 y에 점점 가까워집니다.
흥미로운 점은, 한 샘플에서 강아지일 때는 q 1 만, 고양이일 때는 q 2 만, 소일 때는 q 3 만 직접 로스에 들어간다는 것입니다. 그러나 소프트맥스의 합 1 제약 때문에 한 값을 1에 가깝게 만들면 나머지는 자동으로 0에 가까워지므로, “정답 클래스만 때리면 나머지는 자동으로 줄어든다”는 설명이 가능합니다.


소프트맥스 회귀와 구현 관점
이렇게 소프트맥스를 거친 확률에 대해 크로스 엔트로피를 최소화하는 모델을 소프트맥스 회귀(= 멀티노미얼 로지스틱 회귀)라고 부릅니다. 로짓 L=W ⊤ x+b까지만 보면 선형 회귀이고, 그 뒤의 소프트맥스+크로스엔트로피는 “로스를 만들기 위한 변환”으로 볼 수 있다는 관점도 함께 제시합니다.
파이토치 등에서는 이 관점 때문에 nn.CrossEntropyLoss 안에 소프트맥스가 내장되어 있어, 모델에서는 마지막을 nn.Linear로만 두고 별도의 소프트맥스 레이어를 넣지 말라고 권장합니다.
이렇게 하면 분류 출력에는 크로스 엔트로피, 다른 회귀 출력에는 MSE 등 서로 다른 로스를 동시에 적용하기도 수월해집니다.

[AI 인공지능 머신러닝 딥러닝] - 이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 7강 Universal Approximation Theorem (보편 근사 정리)
이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 7강 Universal Approximation Theorem (보편 근사 정리)
[AI 인공지능 머신러닝 딥러닝] - 이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 - 무료 강의 및 책 소개 이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 - 무료 강의 및 책 소개한국어로 딥러닝 공부해봤다는 사람중
inner-game.tistory.com





