이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 5강 - linear activation, 역전파(Backpropagation)
[AI 인공지능 머신러닝 딥러닝] - 이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 - 무료 강의 및 책 소개
이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 - 무료 강의 및 책 소개
한국어로 딥러닝 공부해봤다는 사람중에 안들어 본 사람이 없을것 같은 이지 딥러닝 시리즈 입니다. 이 강의는 유투브로 제공되며 책도 있습니다. 이지 딥러닝 유투브 강의이지 딥러닝 유투브
inner-game.tistory.com
[Easy! 딥러닝] 5-1강. 인공 신경망을 바라보는 통찰력이 생긴다..! | linear activation이 중간에 들어가면??
이 강의의 핵심은 “인공 신경망은 결국 ‘행렬곱 + 벡터 덧셈 + 비선형 activation’의 반복이며, 중간에 linear activation만 쓰면 아무리 깊게 쌓아도 그냥 한 층짜리 선형 모델과 다를 바 없다”입니다.
1. MLP를 행렬·벡터로 보기
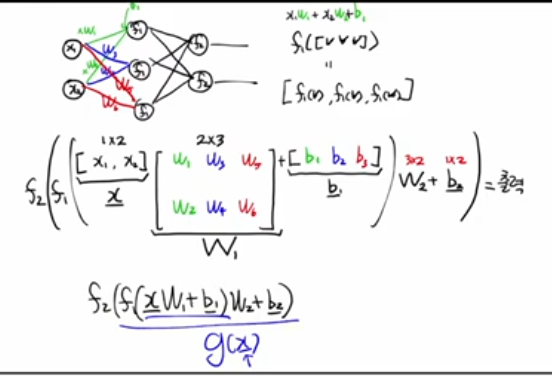
영상에서는 2–3–2 구조의 간단한 MLP를 예로 들어, 각 노드 연결을 일일이 쓰지 않고 행렬·벡터로 압축해서 표현합니다.
- 입력을 행벡터 x = [ x 1 , x 2 ] x=[x 1 ,x 2 ]로 놓고, 첫 번째 레이어의 weight를 W 1 W 1 (예: 2 × 3 2×3), bias를 b 1 b 1 (예: 1 × 3 1×3)라 두면 z 1 = x W 1 + b 1 , a 1 = f 1 ( z 1 ) z 1 =xW 1 +b 1 ,a 1 =f 1 (z 1 ) 처럼 ‘행렬곱 + 벡터 덧셈 + activation’이 하나의 레이어입니다.
- 두 번째 레이어도 동일하게 z 2 = a 1 W 2 + b 2 , a 2 = f 2 ( z 2 ) z 2 =a 1 W 2 +b 2 ,a 2 =f 2 (z 2 ) 로 표현할 수 있고, 이걸 합치면 “입력 → (선형변환 + 비선형함수)의 연속”이라는 큰 하나의 함수 g ( x ) g(x)가 됩니다.
이 관점에서 “shape(차원)”만 알고 있으면, 수식만 보고도 네트워크 구조를 다시 그려낼 수 있다는 통찰을 강조합니다.

2. 왜 비선형 activation이 꼭 필요한가?
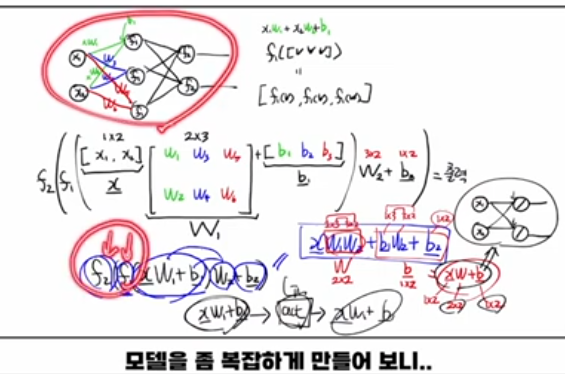
히든 레이어에서 activation이 전부 linear(예: f ( x ) = x f(x)=x)라고 가정하면, 네트워크 전체가 그냥 하나의 선형 변환으로 “압축(collapse)”됩니다.
- 예를 들어, a 1 = x W 1 + b 1 , a 2 = a 1 W 2 + b 2 a 1 =xW 1 +b 1 ,a 2 =a 1 W 2 +b 2 이고 f 1 , f 2 f 1 ,f 2 가 전부 linear라면, 전개하면 a 2 = x ( W 1 W 2 ) + ( b 1 W 2 + b 2 ) a 2 =x(W 1 W 2 )+(b 1 W 2 +b 2 ) 꼴의 하나의 선형식 x W + b xW+b가 됩니다.
- 즉, W 1 , W 2 W 1 ,W 2 두 번 곱한 것과 어떤 하나의 W W를 곱한 것이 표현력 측면에서는 동일하며, “여러 층을 쌓았다”는 이점이 사라집니다.
이건 스칼라 예시 y = A 1 A 2 x + b y=A 1 A 2 x+b vs y = A x + b y=Ax+b와 완전히 같은 논리로, 둘 다 잘 학습되었다면 성능은 똑같고, 굳이 파라미터를 쪼개 쓸 이유가 없습니다.
3. “선형 activation을 쓰면 한 층짜리가 된다” 직관
강의에서는 “레이어 사이에 linear activation만 있으면, 중간 레이어가 고속도로처럼 무시된다”는 비유를 씁니다.
- 여러 개의 linear 레이어: x → W 1 , b 1 → linear → W 2 , b 2 → linear ⋯ x W 1 ,b 1 linear W 2 ,b 2 linear ⋯ 은 항상 x W + b xW+b 하나로 합쳐집니다.
- 결과적으로, 깊이를 늘려도 표현 가능한 함수는 항상 “입력과 출력 사이의 선형 관계”뿐이라, 복잡한 비선형 결정 경계를 만들 수 없습니다.
그래서 “깊게 만들수록 표현력이 올라간다”는 말은 반드시 중간에 비선형 activation(ReLU, tanh 등)이 있을 때만 성립합니다.


4. 그럼 linear activation은 어디에 쓰는가?
영상에서는 “linear activation은 절대 쓰지 말자가 아니라, 쓸 자리가 딱 정해져 있다”는 포인트를 두 가지로 정리합니다.
1. 회귀(regression) 문제의 마지막 층
- 출력이 실수 전체 범위(대략 − ∞ ∼ + ∞ −∞∼+∞)를 가져야 할 때, 마지막 층에 linear activation을 둡니다.
- 예: 집값 예측, 온도 예측 등에서 마지막에 ReLU나 sigmoid를 쓰면 출력 범위가 제한되어 버리므로 부적절합니다.
2. 정보 손실을 줄여야 하는 ‘좁은’ 병목(bottleneck) 층
- ReLU 같은 비선형 함수는 음수 정보를 0으로 날려버려서, 차원이 축소되는 병목 구간에서는 정보가 심하게 손실될 수 있습니다.
- MobileNetV2의 “linear bottleneck” 아이디어가 대표적 예로, 축소된 저차원 표현에서는 굳이 ReLU를 넣지 말고 linear activation으로 그대로 통과시켜 정보를 보존하자는 전략입니다.
즉, 전체적으로는 “히든 레이어에는 비선형 activation을 기본으로 쓰되,
- 회귀 문제의 마지막 출력,
- 매우 좁은 병목층(특히 MobileNetV2 같은 구조) 처럼 일부 특별한 위치에서만 linear activation을 사용한다”는 식으로 정리할 수 있습니다.


정리하면, 인공 신경망은 입력 벡터에 행렬을 곱하고 벡터를 더한 뒤 비선형 activation을 통과시키는 연산을 여러 층 반복하는 구조입니다. 각 층의 연산은 x W + b xW+b 형태의 선형 변환과 그 위에 얹힌 비선형 함수로 이해할 수 있으며, 이 비선형성이 있을 때에만 깊이가 깊어질수록 더 복잡한 함수를 표현할 수 있습니다. 만약 중간 모든 층이 linear activation만 사용한다면, 아무리 많은 층을 쌓아도 전체 네트워크는 결국 하나의 선형 모델과 동일한 표현력만 가지게 되며, 이는 단순 선형 회귀와 같은 수준의 모델일 뿐입니다. 따라서 일반적으로는 히든 레이어에 ReLU와 같은 비선형 activation을 사용하고, 회귀 문제의 마지막 출력층이나 MobileNetV2에서의 linear bottleneck처럼 정보 손실을 줄여야 하는 특수한 위치에서만 linear activation을 사용하는 것이 바람직한 설계입니다.
[Easy! 딥러닝] 5-2강. 역전파(Backpropagation) 세상에서 가장 쉬운 설명!
역전파(Backpropagation): 세상에서 가장 쉬운 설명
혁펜하임 강의에서 배운 역전파는 딥러닝의 핵심으로, 그라디언트 디센트(Gradient Descent)를 통해 가중치(W)를 업데이트하기 위해 손실(Loss)을 각 가중치에 대한 편미분으로 계산하는 과정입니다. 이 과정은 체인 룰(Chain Rule)을 이용해 출력층에서 입력층으로 오차를 뒤로 전파합니다. 고등학교 합성함수 미분만 알면 충분히 이해할 수 있어요.
핵심
액웨액웨액웨액나
역전파(Backpropagation): weight를 업데이트하기 위해 loss를 각 가중치에 대해 편미분하는 과정 gradient가 weight가 나아가야 할 방향을 알려주는 guide이고 그 방향의 반대방향으로 gradient를 업데이트해준다.
왜 역전파가 필요한가?
딥러닝 네트워크가 깊어질수록 깊은 층의 가중치(W1)에 대한 손실 미분이 복잡해집니다. 순전파(Forward Propagation)로 입력을 출력까지 통과시켜 중간 값(a1, z2, a2 등)을 저장한 후, 역전파로 체인 룰을 적용해 효율적으로 계산합니다. 예를 들어, L L을 W 2 W2에 대해 미분할 때는
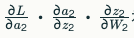
처럼 곱합니다.
가장 기억할 포인트는 "액웨 액웨 액나" 패턴: 마지막 층은 δ = a − y δ=a−y (오차), 이전 층은

(액티베이션 미분 곱하기)입니다. 여러 경로(패스)가 있으면 그라디언트를 더해야 해요.
체인 룰 예제로 이해하기
( x + 1 ) 2 (x+1) 2 미분처럼 f ( g ( x ) ) ′ = f ′ ( g ( x ) ) ⋅ g ′ ( x ) f(g(x)) ′ =f ′ (g(x))⋅g ′ (x) 원리를 네트워크에 적용합니다. 순전파로 z(선형), a(액티베이션), L(MSE: ( y p r e d − y ) 2 (y pred −y) 2 ) 계산 후
역전파:

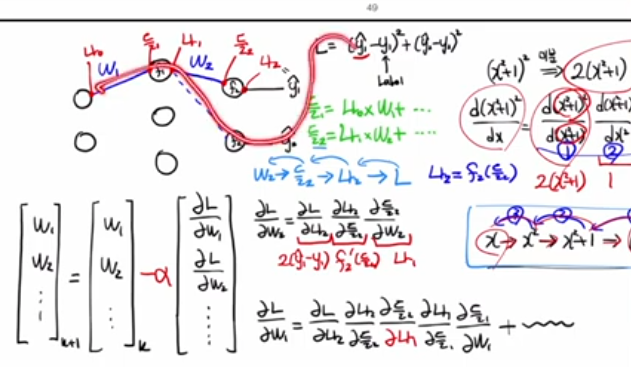


순전파 먼저 하는 이유
역전파 시 중간 값(z, a)이 필요해 순전파를 먼저 실행하고 저장합니다. 이 값을 재사용해 수치 미분 대신 해석적 미분으로 빠르게 계산하죠. 강의처럼 깊은 네트워크에서도 "액웨" 반복으로 모든 가중치 업데이트 가능합니다.


[AI 인공지능 머신러닝 딥러닝] - 이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 6강 시그모이드, 로지스틱 회귀, MSE, 소프트맥스
이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 6강
[AI 인공지능 머신러닝 딥러닝] - 이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 - 무료 강의 및 책 소개 이지 딥러닝 - 혁펜하임 | Easy! 딥러닝 - 무료 강의 및 책 소개한국어로 딥러닝 공부해봤다는 사람중
inner-game.tistory.com





