weekly-contest-212

 

leetcode.com/contest/weekly-contest-212

 

 

 

---

leetcode.com/problems/slowest-key/

class Solution:
    def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:
        #Time complexity = O(n)
        #Space complexity = O(1)
        
        maxletter = keysPressed[0]
        maxvalue = releaseTimes[0]
        
        for i in range(1, len(releaseTimes)):
            value = releaseTimes[i] - releaseTimes[i-1]
            
            if value > maxvalue:
                maxvalue = value
                maxletter = keysPressed[i]
                
            elif value == maxvalue:
                maxletter = max(maxletter, keysPressed[i])
                
        return maxletter
            

---

1630. Arithmetic Subarrays

leetcode.com/problems/arithmetic-subarrays/

 

sort 이용하지말고 정수론 이용해서 짜야할듯

 

O(m x NlogN) -> O(MN)

 

leetcode.com/problems/arithmetic-subarrays/discuss/909120/python3-using-set-no-sort-O(MN)

 

    def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:
        def isArith(n):
            st = set(n)
            if len(n) != len(st): return len(st) == 1 # take care of duplicates
            mx, mn, = max(n), min(n)
            if (mx - mn)%(len(n)-1) != 0: return False
            step = (mx - mn)//(len(n)-1)
            for i in range(mn, mx, step):
                if i not in st:
                    return False
            return True   
        
        return [isArith(nums[start:stop+1]) for start, stop in zip(l,r)]

---

1631. Path With Minimum Effort

leetcode.com/problems/path-with-minimum-effort/

구글기출

 

이 문제를 처음 봤을때 생각난 백트랙킹.. TLE .. 

 

 

Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells.

Hide Hint 2

If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost.

Show Hint 3

Binary search the k value.

 

 

Solution

---

Overview

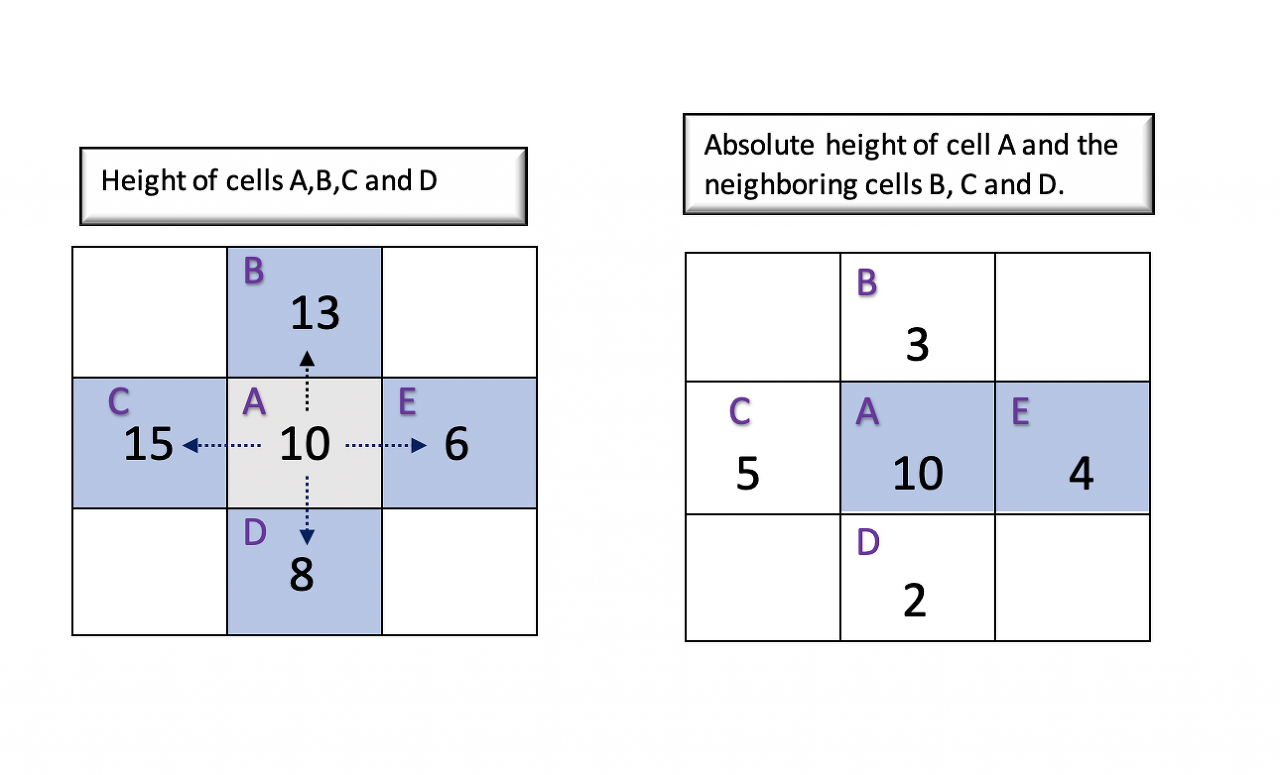
The problem is that given a 2D matrix \text{heights}heights of size \text{row} \cdot \text{col}row⋅col representing the height of each cell, we have travel from top right corner (0, 0) to bottom right corner (row-1, col-1) of the matrix and find a path with minimum effort. The effort to move from one cell to another is the absolute difference in the heights of those cells.

The following example illustrates the effort required to travel from cell A to all the neighboring cells B,C, D, and F. The first matrix represents the heights of each cell and the second represents the absolute difference from cell A to all the adjacent cells. The path with minimum effort is from cell A to cell E.

Let's understand the different approaches to implement the solution in detail.

---

Approach 1: Brute Force using Backtracking

Intuition

The brute force approach would be to traverse all the possible paths from the source cell to the destination cell and track the path with minimum efforts. To try all possible paths, the first thing that comes in our mind is Backtracking. Backtracking incrementally builds the candidates for a solution using depth first search and discards the candidates (backtrack) if it doesn't satisfy the condition.

The backtracking algorithms consists of the following steps,

• Choose: Choose the potential candidate. For any given cell A, we must choose the adjacent cells in all 4 directions (up, down, left, right) as a potential candidate.
• Constraint: Define a constraint that must be satisfied by the chosen candidate. In this case, a chosen cell is valid if it is within the boundaries of the matrix and it is not visited before.
• Goal: We must define the goal that determines if we have found the required solution and we must backtrack. Here, our goal is achieved once we have reached the destination cell. On reaching the destination cell, we must track the maximum absolute difference in that path and backtrack.

To make the algorithm more efficient, once we find any path from source to destination, we track the maximum absolute difference of all adjacent cells in that path in a variable \text{maxSoFar}maxSoFar. With this, we can avoid going into other paths in the future where effort is greater than or equal to \text{maxSoFar}maxSoFar.

In other words, if we have already found a path to reach the destination cell with \text{maxSoFar}maxSoFar, then, we would only explore other paths if it takes efforts less than \text{maxSoFar}maxSoFar.

Algorithm

We must begin the Depth First Search traversal from source cell (x = 0 and y = 0). Using the intuition discussed above, we must explore all the potential paths using the following steps,

• For a given cell (x, y), explore the adjacent cells in all the 4 directions defined by directions and choose the one with minimum effort.
• The maxDifference keeps track of the maximum absolute difference seen so far in the current path. On every move to the adjacent cell, we must update the maxDifference if it is lesser than the currentDifference (The absolute difference between current cell(x, y) and adjacent cell(adjacentX, adjacentY)).
• We must backtrack from the depth first search traversal once we reach the destination cell (row-1) and (col-1) and return the maximum absolute difference of the current path.

Thus, for each cell, we recursively calculate the effort required to reach the destination cell from all the adjacent cells and find the minimum effort.

Note

It must be noted that we mark the current cell as visited by setting the height of the current cell (x,y) as 0. We must update the height back to the previous value once we backtrack from the current path. This is necessary because the cell must be visited again for other paths.

Implementation

class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        r = len(heights)
        c = len(heights[0])
        self.max_so_far = math.inf
        
        def dfs(x, y, max_diff):
            if x == r-1 and y == c-1:
                self.max_so_far = min(self.max_so_far, max_diff)
                return max_diff
            
            curr_height = heights[x][y]
            min_effort = math.inf
            
            heights[x][y] = -1
            for dx, dy in [[0, 1], [1, 0], [0, -1], [-1, 0]]:
                next_x = x + dx
                next_y = y + dy
                if 0 <= next_x < r and 0 <= next_y < c and heights[next_x][next_y] != -1:
                    curr_diff = max(max_diff, abs(heights[next_x][next_y] - curr_height))
                    if curr_diff < self.max_so_far:
                        result = dfs(next_x, next_y, curr_diff)
                        min_effort = min(min_effort, result)
            heights[x][y] = curr_height
            return min_effort
        
        return dfs(0, 0, 0)

 

Complexity Analysis

Let mm be the number of rows and nn be the number of columns in the matrix \text{heights}heights.

• Time Complexity : \mathcal{O}(3^{m \cdot n})O(3m⋅n). The total number of cells in the matrix is given by m \cdot nm⋅n. For the backtracking, there are at most 4 possible directions to explore, but further, the choices are reduced to 3 (since we won't go back to where we come from). Thus, considering 3 possibilities for every cell in the matrix the time complexity would be \mathcal{O}(3^{m \cdot n})O(3m⋅n).

The time complexity is exponential, hence this approach is exhaustive and results in Time Limit Exceeded (TLE).

• Space Complexity: \mathcal{O}(m \cdot n)O(m⋅n) This space will be used to store the recursion stack. As we recursively move to the adjacent cells, in the worst case there could be m \cdot nm⋅n cells in the recursive call stack.

---

Approach 2: Variations of Dijkstra's Algorithm

Intuition

The previous approach is exhaustive as it traverses all the paths. If we observe, the problem is similar to finding the shortest path from a source cell to a destination cell. Here, the shortest path is the one with minimum absolute difference between every adjacent cells in that path. Also, since there is height associated with each cell, simple BFS traversal won't be sufficient.

The absolute difference between adjacent cells A and B can be perceived as the weight of an edge from cell A to cell B. Thus, we could use Dijkstra's Algorithm which is used to find the shortest path in a weighted graph with a slight modification of criteria for the shortest path.

Let's look at the algorithm in detail.

 

Algorithm

• We use a differenceMatrix of size \text{row} \cdot \text{col}row⋅col where each cell represents the minimum effort required to reach that cell from all the possible paths. Also, initialize we all the cells in the differenceMatrix to infinity \text{(MAX\_INT)}(MAX_INT) since none of the cells are reachable initially.

• As we start visiting each cell, all the adjacent cells are now reachable. We update the absolute difference between the current cell and adjacent cells in the differenceMatrix. At the same time, we also push all the adjacent cells in a priority queue. The priority queue holds all the reachable cells sorted by its value in differenceMatrix, i.e the cell with minimum absolute difference with its adjacent cells would be at the top of the queue.

• We begin by adding the source cell (x=0, y=0) in the queue. Now, until we have visited the destination cell or the queue is not empty, we visit each cell in the queue sorted in the order of priority. The less is the difference value(absolute difference with adjacent cell) of a cell, the higher is its priority.

  • Get the cell from the top of the queue curr and visit the current cell.

  • For each of the 4 cells adjacent to the current cell, calculate the maxDifference which is the maximum absolute difference to reach the adjacent cell (adjacentX, adjacentY) from current cell (curr.x, curr.y).

  • If the current value of the adjacent cell (adjacentX, adjacentY) in the difference matrix is greater than the maxDifference, we must update that value with maxDifference. In other words, we have found that the path from the current cell to the adjacent cell takes lesser efforts than the other paths that have reached the adjacent cell so far. Also, we must add this updated difference value in the queue.

Ideally, for updating the priority queue, we must delete the old value and reinsert with the new maxDifference value. But, as we know that the updated maximum value is always lesser than the old value and would be popped from the queue and visited before the old value, we could save time and avoid removing the old value from the queue.

• At the end, the value at differenceMatrix[row - 1][col - 1] is the minimum effort required to reach the destination cell (row-1,col-1).

 

 

1 / 8

Implementation

 

 

Complexity Analysis

• Time Complexity : \mathcal{O}(m \cdot n \log (m \cdot n))O(m⋅nlog(m⋅n)), where mm is the number of rows and nn is the number of columns in matrix \text{heights}heights. It will take \mathcal{O}(m \cdot n)O(m⋅n) time to visit every cell in the matrix. The priority queue will contain at most m \cdot nm⋅n cells, so it will take \mathcal{O}(\log (m \cdot n))O(log(m⋅n)) time to re-sort the queue after every adjacent cell is added to the queue. This given as total time complexiy as \mathcal{O}(m \cdot n \log(m \cdot n))O(m⋅nlog(m⋅n)).

• Space Complexity: \mathcal{O}(m \cdot n)O(m⋅n), where mm is the number of rows and nn is the number of columns in matrix \text{heights}heights. The maximum queue size is equal to the total number of cells in the matrix \text{height}height which is given by m \cdot nm⋅n. Also, we use a difference matrix of size m \cdot nm⋅n. This gives as time complexity as \mathcal{O}(m \cdot n + m \cdot n)O(m⋅n+m⋅n) = \mathcal{O}(m \cdot n)O(m⋅n)

---

Approach 3: Union Find - Disjoint Set

Intuition

Using Disjoint Set is another intuitive way to solve the problem. Each cell in the matrix is a single node/component in a graph. The path from the current cell to adjacent cells is an edge connecting the 2 cells. Using this intuition, we could use Union Find algorithm to form a connected component from the source cell to the destination cell.

Initially, every cell is a disconnected component and we aim to form a single connected component that connects the source cell to the destination cell. Each connected component connects multiple cells and is identified by a parent. We must continue connecting components until the source cell and destination cell shares the same parent.

The union find algorithm performs 2 operations,

Find(x): Returns the parent of the connected component to which x belongs.

Union(x, y): Merges the two disconnected components to which x and y belongs.

To efficiently implement the above operations, we could use Union By Rank and Path Compression strategy.

Algorithm

• Initially, each cell is a disconnected component, so we initialize each cell as a parent of itself. Also we flatten a 2D matrix into a 1D matrix of size row * col and each cell (currentRow, currentCol) in a 2D matrix can be stored at (currentRow * col + currentCol) in a 1D matrix. The below figure illustrates this idea.

• We also build an edgeList which consists of the absolute difference between every adjacent cell in the matrix. We also sort the edge list in non-decreasing order of difference. The below example illustrates the edge list of given heights matrix [[1,2,2],[3,8,2],[5,3,5]] sorted by difference.

• Start iterating over the sorted edge list and connect each edge to form a connected component using Union Find Algorithm.

• After every union, check if the source cell (0) and destination cell (row * col - 1) are connected. If yes, the absolute difference between the current edge is our result. Since we access the edges in increasing order of difference, and the current edge connected the source and destination cell, we are sure that the current difference is the maximum absolute difference in our path with minimum efforts.

Implementation

 

 

Complexity Analysis

Let mm be the number of rows and nn be the number of columns of the matrix \text{height}height.

• Time Complexity : \mathcal{O}(m\cdot n(\log(m\cdot n)))O(m⋅n(log(m⋅n))). We iterate each edge in the matrix. From the above example, it is evident that for a matrix of size 3 \cdot33⋅3, the total number of edges are 1212. Thus, for a m \cdot nm⋅n matrix, the total number of edges could be given by (m\cdot n \cdot 2)-(m+n)(m⋅n⋅2)−(m+n) (3*3*2) - (3+3)), which is roughly equivalent to m \cdot nm⋅n.

For every edge, we find the parent of each cell and perform the union (Union Find). For nn elements, the time complexity of Union Find is \log nlogn. (Refer Proof Of Time Complexity Of Union Find). Thus for m \cdot nm⋅n cells, the time taken to perform Union Find would be \log m \cdot nlogm⋅n. This gives us total time complexity as, \mathcal{O}(m\cdot n(\log(m\cdot n)))O(m⋅n(log(m⋅n))).

• Space Complexity : \mathcal{O}(m \cdot n)O(m⋅n) , we use arrays edgeList, parent, and rank of size m \cdot nm⋅n.

---

Approach 4: Binary Search Using BFS

Intuition

Our aim to find the minimum effort required to travel from source cell to destination cell. We know from the given constraints that the maximum height could be 10^6 (1000000)106(1000000). So we know that our required absolute difference values would between 00 and 10^6106. We could use Binary Search and reduce our search space by half.

Given the lower bound as 00 and upper bound as 10^6106, we could repeatedly calculate the middle value. Let this middle value be mid. We could divide our search space based on the following condition,

• If there exists a path from the source cell to the destination cell with the effort less than the value mid, we know that the required minimum effort value lies between lower bound 00 and mid.
• Similarly, if there doesn't exist any path from a source cell to destination cell with the effort less than the value mid, we know that the required minimum effort value lies between mid and upper bound 10^6106 .

To find if there exists a path from the source cell to the destination cell for a given mid value, we could use simple graph traversal. In this approach, we use Breath First Search traversal.

Algorithm

• Intialize the lower bound left as 00 and upper bound right as 10^6106. Calculate the middle value mid of the left and right value.

• Using Breath First Search, check if there exists a path from source cell (x=0, y=0) to destination cell (x=row-1, y=column-1) with effort less than or equal to mid using method canReachDestination which returns a boolean value.

• If there exists a path from the source cell to the destination cell, we must update the result value as a minimum of the current result and mid and continue the search in the range between left and mid-1. For this, we must update the value of right to mid-1.

  Otherwise, we must search in the range between mid+1 and right and update left to mid+1.

Implementation

 

 

Complexity Analysis

Let mm be the number of rows and nn be the number of columns for the matrix \text{height}height.

• Time Complexity : \mathcal{O}(m \cdot n)O(m⋅n). We do a binary search to calculate the mid values and then do Breadth First Search on the matrix for each of those values.

Binary Search:To perform Binary search on numbers in range (0.. 10^{6})(0..106), the time taken would be \mathcal{O}(\log 10^{6})O(log106).

Breath First Search: The time complexity for the Breadth First Search for vertices V and edges E is \mathcal{O}(V+E)O(V+E) (Refer) Thus, in the matrix of size m \cdot nm⋅n, with m \cdot nm⋅n vertices and m \cdot nm⋅n edges (Refer time complexity of Approach 3), the time complexity to perform Breath First Search would be \mathcal{O}(m \cdot n + m \cdot n)O(m⋅n+m⋅n) = \mathcal{O}(m \cdot n)O(m⋅n).

This gives us total time complexity as \mathcal{O}(\log10^{6}\cdot(m \cdot n))O(log106⋅(m⋅n)) which is equivalent to \mathcal{O}(m \cdot n)O(m⋅n).

• Space Complexity: \mathcal{O}(m \cdot n)O(m⋅n), as we use a queue and visited array of size m \cdot nm⋅n

---

Approach 5: Binary Search Using DFS

Intuition and Algorithm

The solution is similar to Approach 4. Except that, here, we use a Depth First Search traversal to find if there exists a path from the source cell to destination cell for a given value middle value mid.

 

Implementation

 

 

Complexity Analysis

• Time Complexity : \mathcal{O}(m \cdot n)O(m⋅n). As in Approach 4. The only difference is that we are using Depth First Search instead of Breadth First Search and have similar time complexity.

• Space Complexity: \mathcal{O}(m \cdot n)O(m⋅n), As in Approach 4. In Depth First Search, we use the internal call stack (instead of the queue in Breadth First Search).

---

 

관련문제 미디움

1102. Path With Maximum Minimum Value

 

leetcode.com/problems/path-with-maximum-minimum-value/

---

1632. Rank Transform of a Matrix

 

leetcode.com/problems/rank-transform-of-a-matrix/

구글옛날기출

 

 

 

 

---

관련문제 이지

 

1331. Rank Transform of an Array

leetcode.com/problems/rank-transform-of-an-array/

 

 

    def arrayRankTransform(self, A):
        rank = {}
        for a in sorted(A):
            rank.setdefault(a, len(rank) + 1)
        return map(rank.get, A)

 

    def arrayRankTransform(self, A):
        return map({a: i + 1 for i, a in enumerate(sorted(set(A)))}.get, A)