weekly-contest-220
leetcode.com/contest/weekly-contest-220
class Solution:
def reformatNumber(self, number: str) -> str:
ans = ""
chunk = ""
for n in number:
if n.isdigit():
chunk += n
if len(chunk) % 3 == 0:
if len(ans) != 0:
ans += '-'
ans += chunk
chunk = ""
if len(chunk) == 1:
chunk = ans[-1] + chunk
ans = ans[:-1]
if len(chunk) > 0:
if len(ans) != 0:
ans += '-'
ans += chunk
return ans
1695. Maximum Erasure Value
leetcode.com/problems/maximum-erasure-value/
class Solution:
def maximumUniqueSubarray(self, nums: List[int]) -> int:
left = 0
u = set()
u.add(nums[left])
max_sum = u_sum = nums[left]
for i in range(1, len(nums)):
while nums[i] in u:
u.remove(nums[left])
u_sum -= nums[left]
left += 1
u.add(nums[i])
u_sum += nums[i]
max_sum = max(max_sum, u_sum)
return max_sum
1696. Jump Game VI
leetcode.com/problems/jump-game-vi/
Jump game series 점프게임 시리즈
점프게임 시리즈 공부하기: leetcode.com/problemset/all/?search=jump%20game 6개나 있네 2,4 가 구글 기출문제이다. leetcode.com/problems/jump-game/ 내 코드 class Solution: def canJump(self, nums: List[i..
inner-game.tistory.com
1697. Checking Existence of Edge Length Limited Paths
leetcode.com/problems/checking-existence-of-edge-length-limited-paths/
구글기출
An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes.
Given an array queries, where queries[j] = [pj, qj, limitj], your task is to determine for each queries[j] whether there is a path between pj and qj such that each edge on the path has a distance strictly less than limitj .
Return a boolean array answer, where answer.length == queries.length and the jth value of answer is true if there is a path for queries[j] is true, and false otherwise.
Example 1:
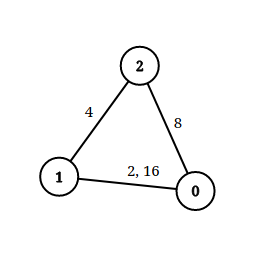
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]] Output: [false,true] Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16. For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query. For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
Example 2:
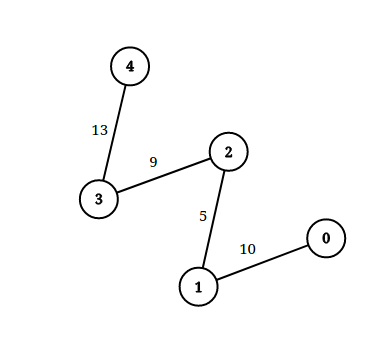
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]] Output: [true,false] Exaplanation: The above figure shows the given graph.
Constraints:
- 2 <= n <= 105
- 1 <= edgeList.length, queries.length <= 105
- edgeList[i].length == 3
- queries[j].length == 3
- 0 <= ui, vi, pj, qj <= n - 1
- ui != vi
- pj != qj
- 1 <= disi, limitj <= 109
- There may be multiple edges between two nodes.
All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations?
Sort queries based on weight and sort edges based on weight as well. Scan through queries from lowest to highest weight and connect the edges whose weight strictly fall below this limit. Check if the queried nodes p and q are connected in Union-Find structure. If so, put True in the relevant position; otherwise put False.
class UnionFind:
def __init__(self, N: int):
self.parent = list(range(N))
self.rank = [1] * N
def find(self, p: int) -> int:
if p != self.parent[p]:
self.parent[p] = self.find(self.parent[p])
return self.parent[p]
def union(self, p: int, q: int) -> bool:
prt, qrt = self.find(p), self.find(q)
if prt == qrt: return False
if self.rank[prt] > self.rank[qrt]:
prt, qrt = qrt, prt
self.parent[prt] = qrt
self.rank[qrt] += self.rank[prt]
return True
class Solution:
def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:
queries = sorted((w, p, q, i) for i, (p, q, w) in enumerate(queries))
edgeList = sorted((w, u, v) for u, v, w in edgeList)
uf = UnionFind(n)
ans = [None] * len(queries)
ii = 0
for w, p, q, i in queries:
while ii < len(edgeList) and edgeList[ii][0] < w:
_, u, v = edgeList[ii]
uf.union(u, v)
ii += 1
ans[i] = uf.find(p) == uf.find(q)
return ans Analysis
Time complexity O(NlogN) + O(MlogM)
Space complexity O(N)





