941. Valid Mountain Array

leetcode.com/problems/valid-mountain-array/

 

941. Valid Mountain Array

Easy

57981Add to ListShare

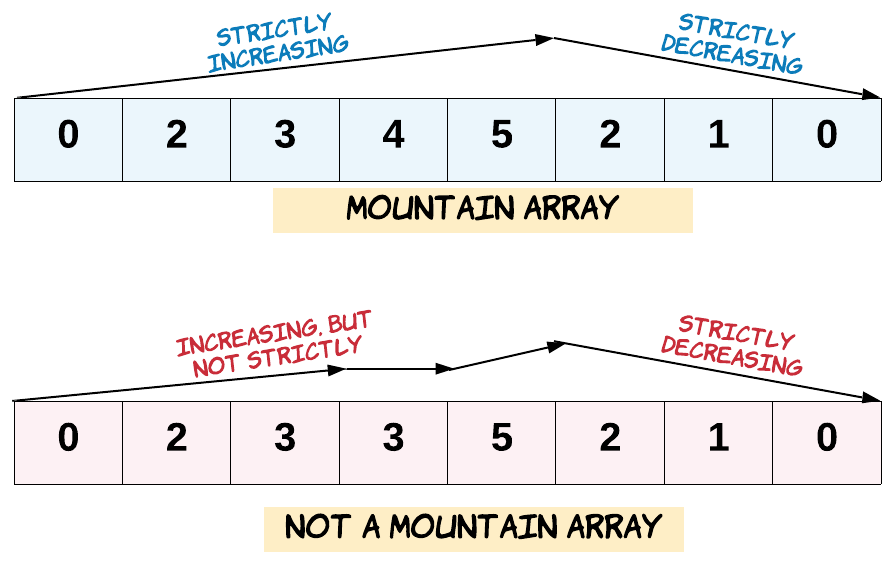
Given an array of integers arr, return true if and only if it is a valid mountain array.

Recall that arr is a mountain array if and only if:

• arr.length >= 3
• There exists some i with 0 < i < arr.length - 1 such that:
  • arr[0] < arr[1] < ... < arr[i - 1] < A[i]
  • arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

 

Example 1:

Input: arr = [2,1] Output: false

Example 2:

Input: arr = [3,5,5] Output: false

Example 3:

Input: arr = [0,3,2,1] Output: true

 

Constraints:

• 1 <= arr.length <= 104
• 0 <= arr[i] <= 104

 

 

Solution

---

Approach 1: One Pass

Intuition

If we walk along the mountain from left to right, we have to move strictly up, then strictly down.

Algorithm

Let's walk up from left to right until we can't: that has to be the peak. We should ensure the peak is not the first or last element. Then, we walk down. If we reach the end, the array is valid, otherwise its not.

 

 

class Solution {
    public boolean validMountainArray(int[] A) {
        int N = A.length;
        int i = 0;

        // walk up
        while (i+1 < N && A[i] < A[i+1])
            i++;

        // peak can't be first or last
        if (i == 0 || i == N-1)
            return false;

        // walk down
        while (i+1 < N && A[i] > A[i+1])
            i++;

        return i == N-1;
    }
}

 

 

Complexity Analysis

• Time Complexity: O(N)O(N), where NN is the length of A.

• Space Complexity: O(1)O(1).

 

 

 

위 솔루션의 방법은 추가 스테이터스가 필요없어서 더 좋은듯

 

class Solution {
    public boolean validMountainArray(int[] arr) {
        if(arr.length < 3) return false;
        
        int status = -1;
        for(int i = 0; i < arr.length-1; i++) {
            if((status == -1 || status == 0) && arr[i] < arr[i+1]) {
                status = 0;
            } else if((status == 0 || status == 1) && arr[i] > arr[i+1]) {
                status = 1;
            } else {
                return false;
            }
        }
        
        return (status == 1);
    }
}