80. Remove Duplicates from Sorted Array II

leetcode.com/problems/remove-duplicates-from-sorted-array-ii/

2번 방법으로 풀어야함.

Given a sorted array nums, remove the duplicates in-place such that duplicates appeared at most twice and return the new length.

Do not allocate extra space for another array; you must do this by modifying the input array in-place with O(1) extra memory.

Clarification:

Confused why the returned value is an integer, but your answer is an array?

Note that the input array is passed in by reference, which means a modification to the input array will be known to the caller.

Internally you can think of this:

// nums is passed in by reference. (i.e., without making a copy) int len = removeDuplicates(nums); // any modification to nums in your function would be known by the caller. // using the length returned by your function, it prints the first len elements. for (int i = 0; i < len; i++) { print(nums[i]); }

Example 1:

Input: nums = [1,1,1,2,2,3] Output: 5, nums = [1,1,2,2,3] Explanation: Your function should return length = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively. It doesn't matter what you leave beyond the returned length.

Example 2:

Input: nums = [0,0,1,1,1,1,2,3,3] Output: 7, nums = [0,0,1,1,2,3,3] Explanation: Your function should return length = 7, with the first seven elements of nums being modified to 0, 0, 1, 1, 2, 3 and 3 respectively. It doesn't matter what values are set beyond the returned length.

Constraints:

0 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums is sorted in ascending order.

Solution

Approach 1: Popping Unwanted Duplicates

Intuition

The input array is already sorted and hence, all the duplicates appear next to each other. The problem statement mentions that we are not allowed to use any additional space and we have to modify the array in-place. The easiest approach for in-place modifications would be to get rid of all the unwanted duplicates. For every number in the array, if we detect > 2 duplicates, we simply remove them from the list of elements and we do this for all the elements in the array.

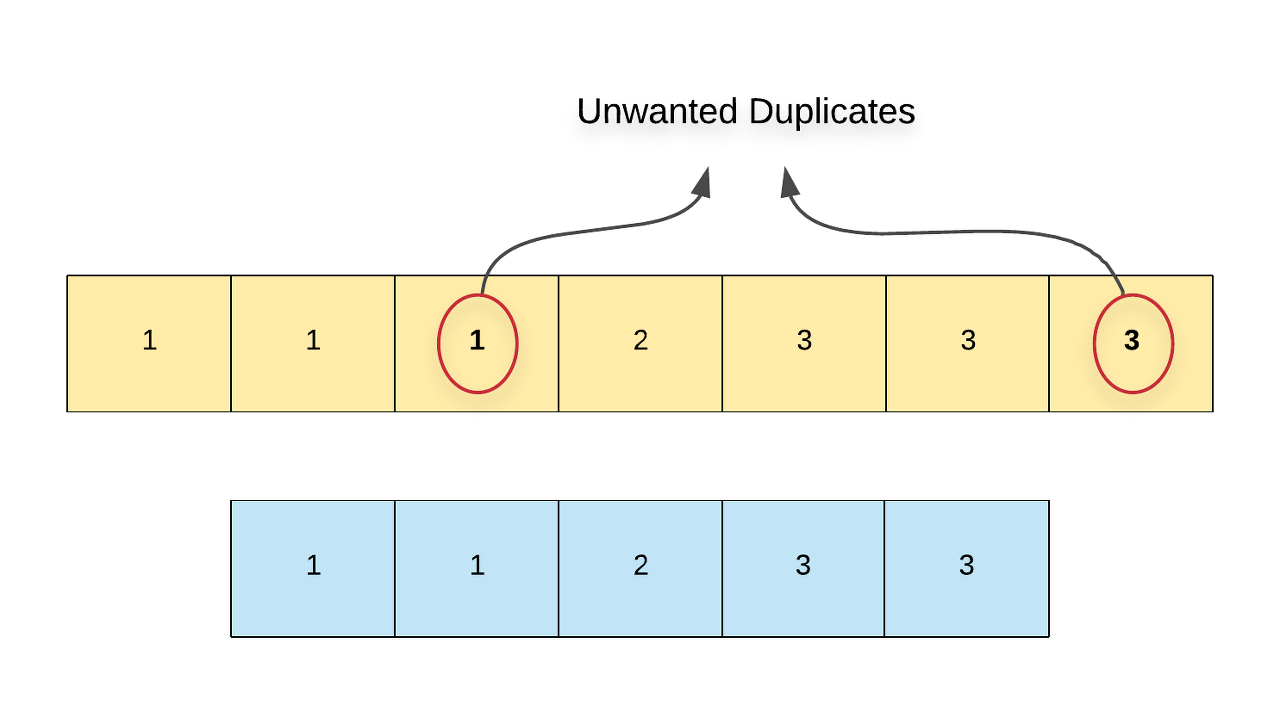
Algorithm

The implementation is slightly tricky so to say since we will be removing elements from the array and iterating over it at the same time. So, we need to keep updating the array's indexes as and when we pop an element else we'll be accessing invalid indexes.
Say we have two variables, i which is the array pointer and count which keeps track of the count of a particular element in the array. Note that the minimum count would always be 1.
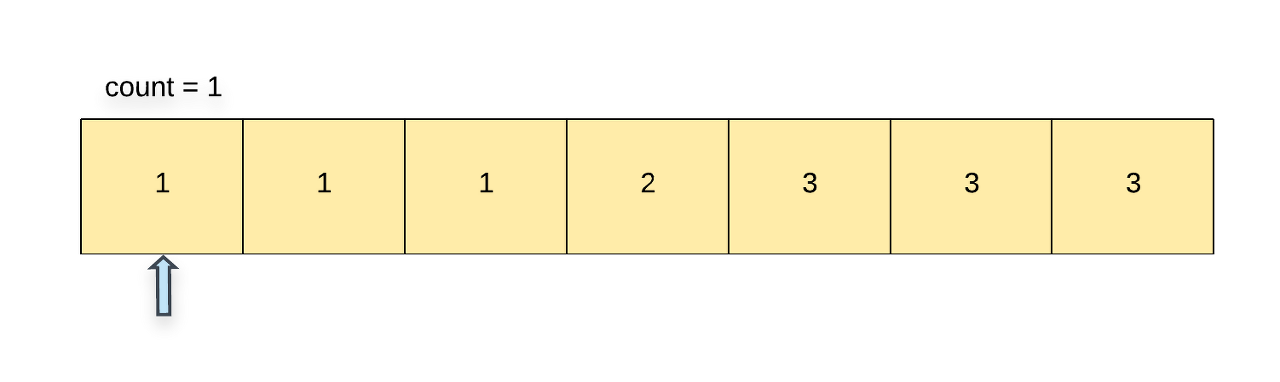
We start with index 1 and process one element at a time in the array.
If we find that the current element is the same as the previous element i.e. nums[i] == nums[i - 1], then we increment the count. If the value of count > 2, then we have encountered an unwanted duplicate element and we can remove it from the array. Since we know the index of this element, we can use the del or pop or remove operation (or whatever corresponding operation is supported in your language of choice) to delete the element at index i from the array. Since we popped an element, we decrement the index by 1 as well.
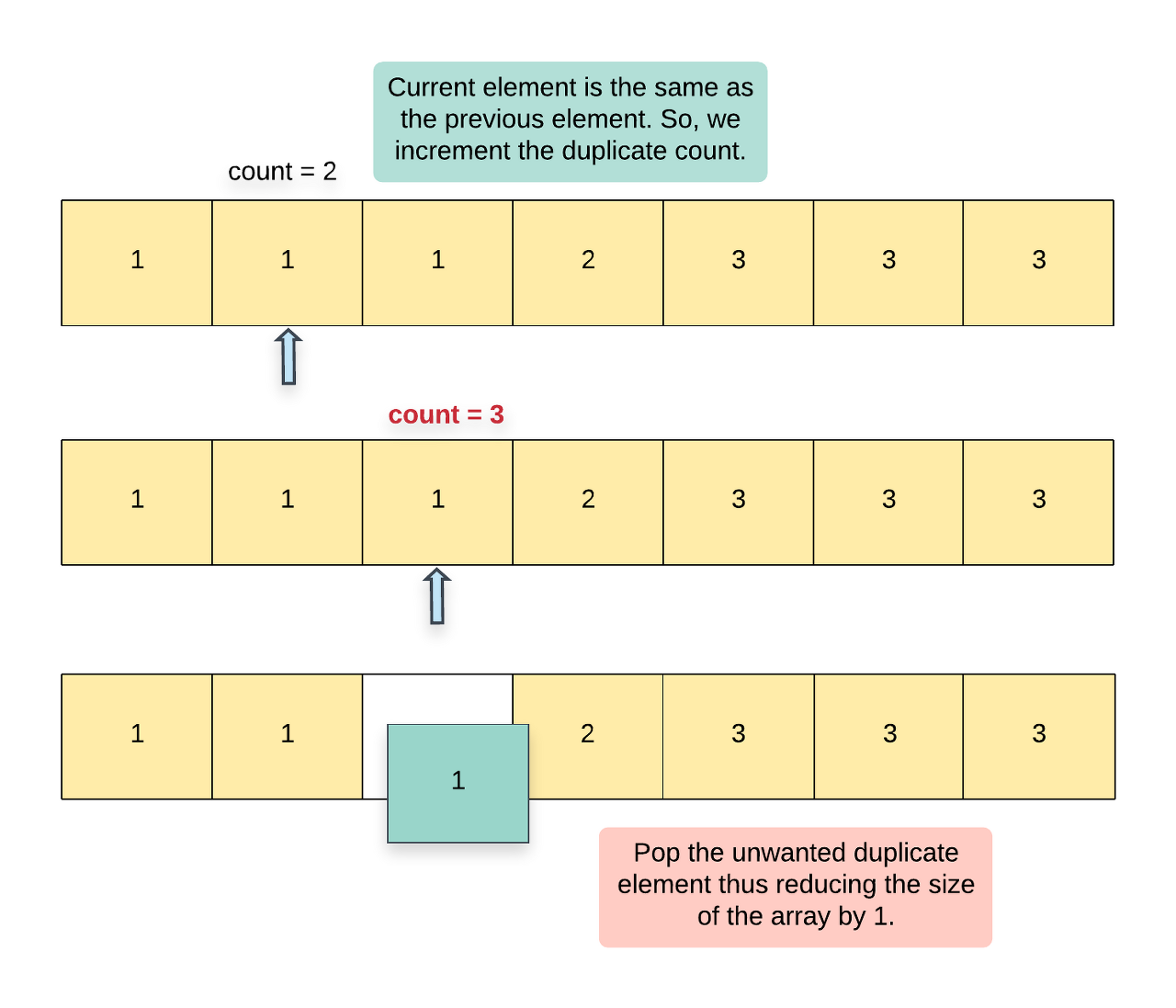
If we encounter that the current element is not the same as the previous element i.e. nums[i] != nums[i - 1], then it means we have a new element at hand and so accordingly, we update count = 1.
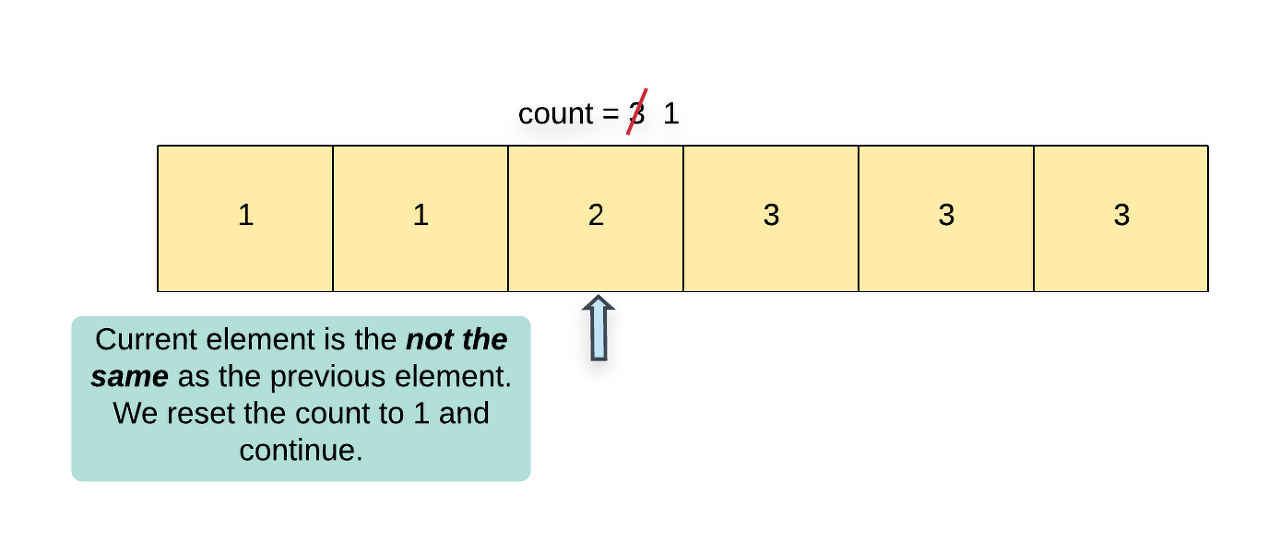
Since we are removing all the unwanted duplicates from the original array, the final array that remains after process all the elements will only contain the valid elements and hence we simply return the length of this array.

Complexity Analysis

Time Complexity: Let's see what the costly operations in our array are:
- We have to iterate over all the elements in the array. Suppose that the original array contains N elements, the time taken here would be O(N).
- Next, for every unwanted duplicate element, we will have to perform a delete operation and deletions in arrays are also O(N).
- The worst case would be when all the elements in the array are the same. In that case, we would be performing N - 2 deletions thus giving us O(N^2) complexity for deletions
- Overall complexity = O(N) + O(N^2) \equiv O(N^2).
Space Complexity: O(1) since we are modifying the array in-place.

Approach 2: Overwriting unwanted duplicates

Intuition

The second approach is really inspired by the fact that the problem statement asks us to return the new length of the array from the function. If all we had to do was remove elements, the function would not really ask us to return the updated length. However, in our scenario, this is really an indication that we don't need to actually remove elements from the array. Instead, we can do something better and simply overwrite the duplicate elements that are unwanted.

We won't be able to achieve this using a single pointer. We will be using a two-pointer approach where one pointer iterates over the original set of elements and another one that keeps track of the next "empty" location in the array or the next location that can be overwritten in the array.

Algorithm

We define two pointers, i and j for our algorithm. The pointer i iterates of the array processing one element at a time and j keeps track of the next location in the array where we can overwrite an element.
We also keep a variable count which keeps track of the count of a particular element in the array. Note that the minimum count would always be 1.
We start with index 1 and process one element at a time in the array.
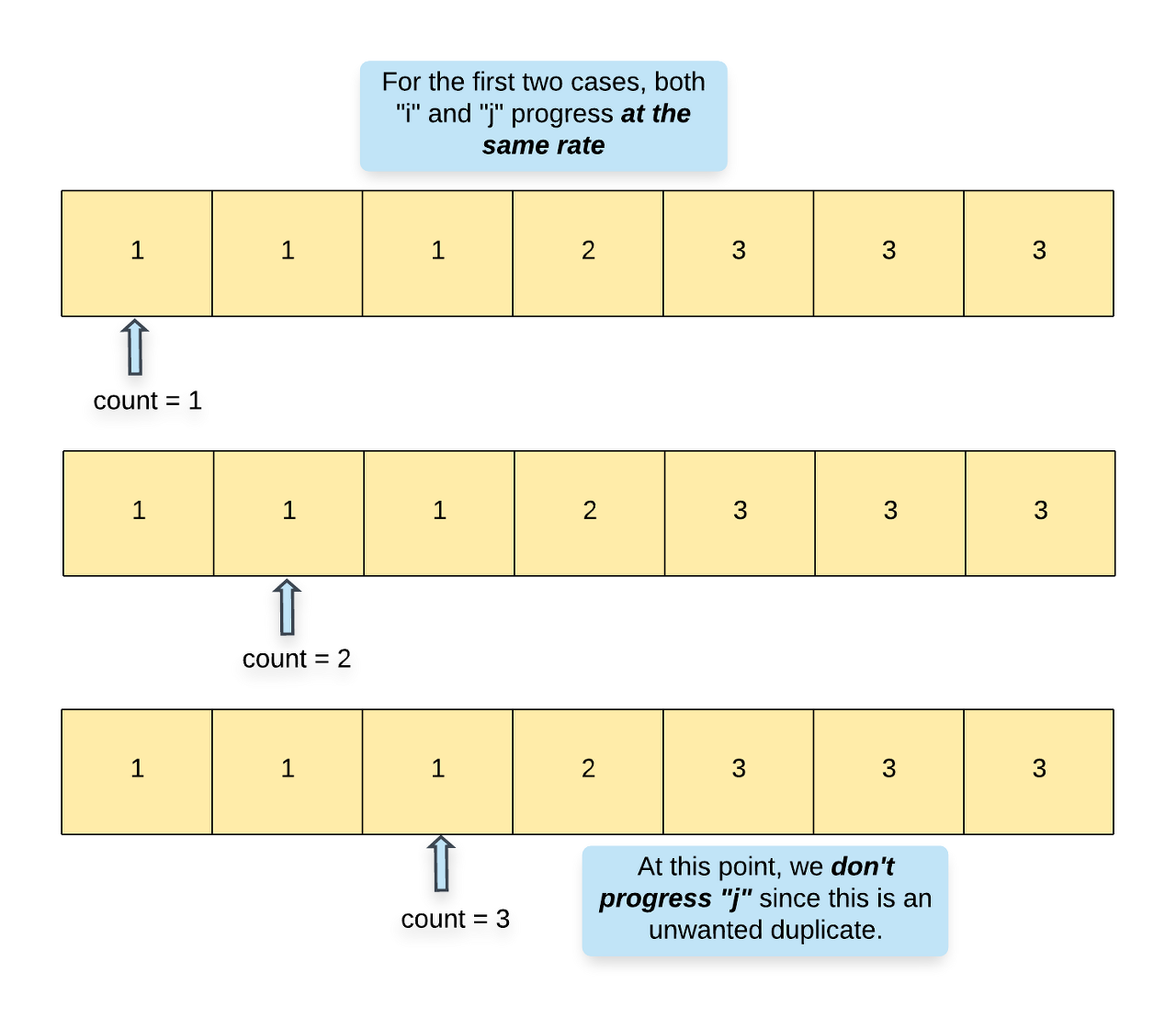
If we find that the current element is the same as the previous element i.e. nums[i] == nums[i - 1], then we increment the count. If the value of count > 2, then we have encountered an unwanted duplicate element. In this case, we simply move forward i.e. we increment i but not j.
However, if the count is <= 2, then we can move the element from index i to index j.
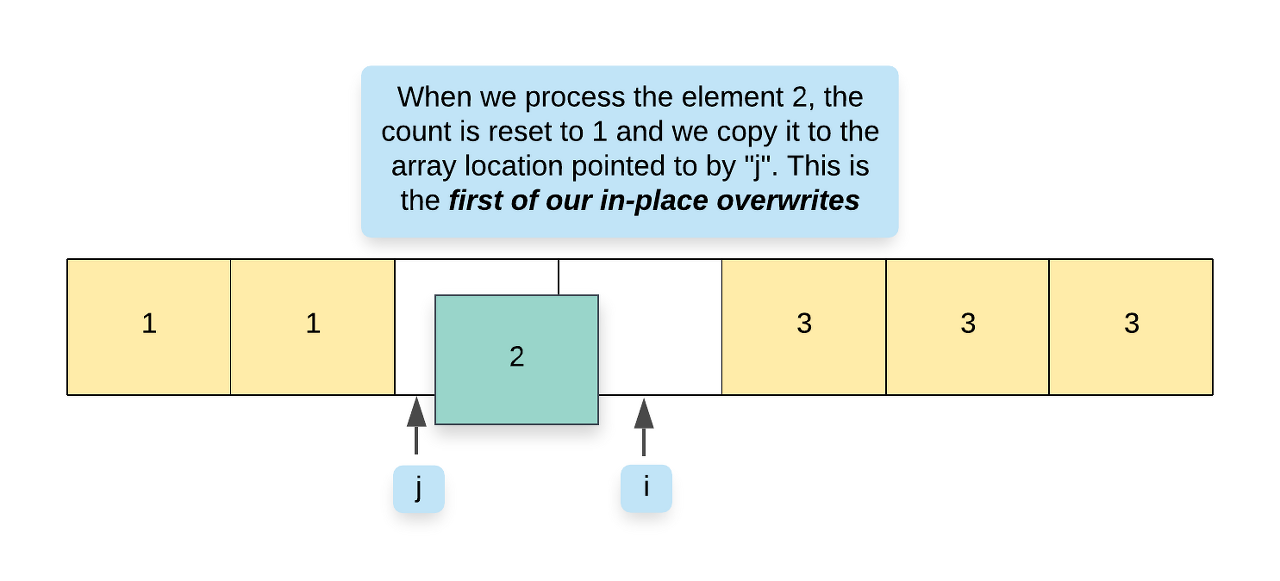
If we encounter that the current element is not the same as the previous element i.e. nums[i] != nums[i - 1], then it means we have a new element at hand and so accordingly, we update count = 1 and also move this element to index j.
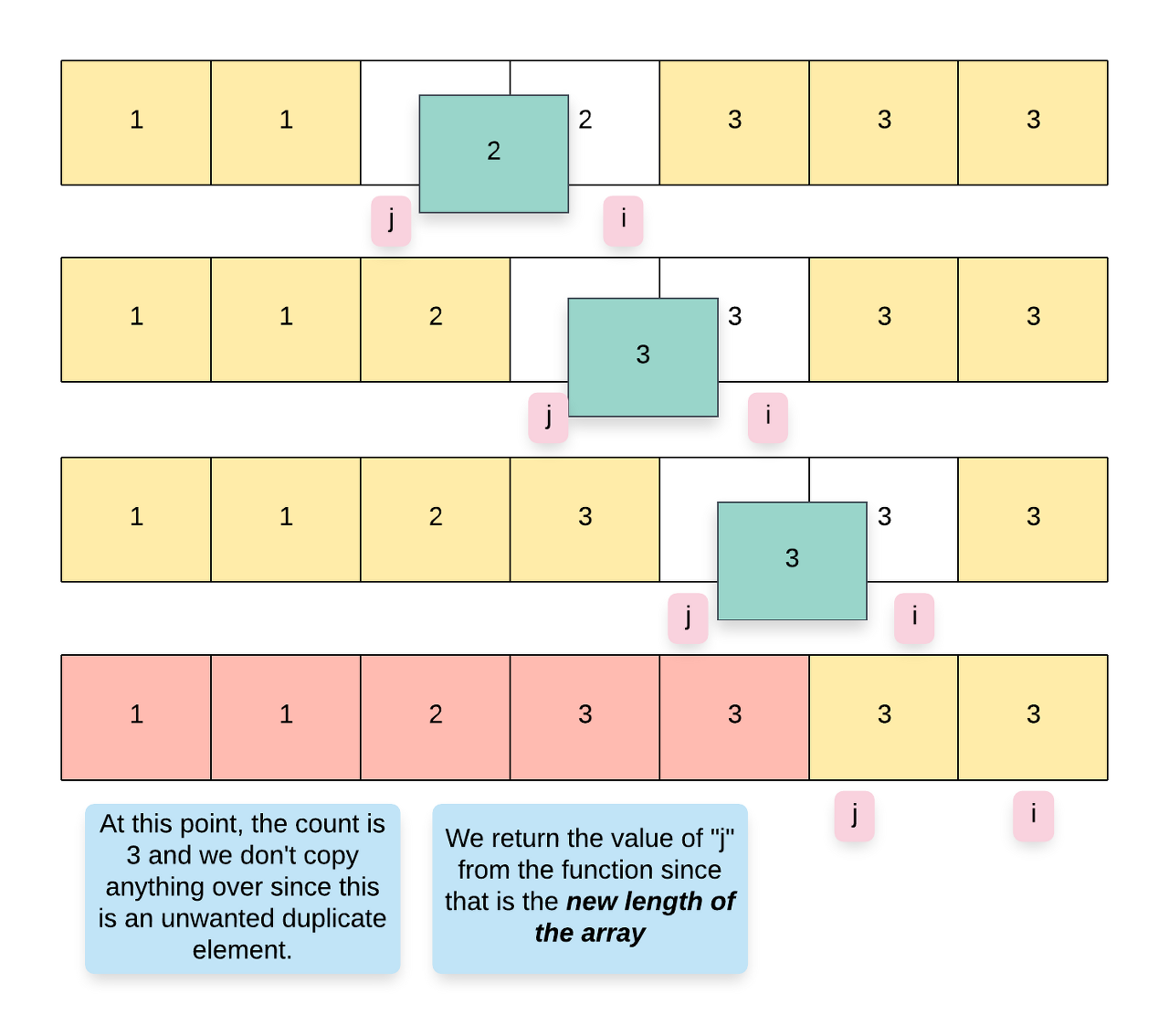
It goes without saying that whenever we copy a new element to nums[j], we have to update the value of j as well since j always points to the location where the next element can be copied to in the array.

class Solution {
    
    public int removeDuplicates(int[] nums) {
        
        //
        // Initialize the counter and the second pointer.
        //
        int j = 1, count = 1;
        
        //
        // Start from the second element of the array and process
        // elements one by one.
        //
        for (int i = 1; i < nums.length; i++) {
            
            //
            // If the current element is a duplicate, increment the count.
            //
            if (nums[i] == nums[i - 1]) {
                
                count++;
                
            } else {
                
                //
                // Reset the count since we encountered a different element
                // than the previous one.
                //
                count = 1;
            }
            
            //
            // For a count <= 2, we copy the element over thus
            // overwriting the element at index "j" in the array
            //
            if (count <= 2) {
                nums[j++] = nums[i];
            }
        }
        return j;
    }
}

Complexity Analysis

Time Complexity: O(N) since we process each element exactly once.
Space Complexity: O(1).

class Solution {
    public int removeDuplicates(int[] nums) {
        int cnt = 0;
        
        int diff = -1;
        for(int i = 1; i < nums.length; i++) {
            if(nums[i] - nums[i-1] == 0 && diff == 0) {
                cnt++;
            }
            diff = nums[i] - nums[i-1];
            nums[i-cnt] = nums[i];
        }
        
        return nums.length-cnt;
    }
}

내 코드를 정답과 비교해 볼때, for문은 잘 구성하였다.

diff라는 status를 이용하기 보단, 그냥 똑같은 문자의 count가 더 깔끔한거 같긴하다.

j와 count변수의 관계 설정이 조금 어려웠던듯.