딥러닝 - 크로스 엔트로피(Cross Entropy) 손실함수

728x90

크로스 엔트로피(Cross Entropy)는 딥러닝과 머신러닝 분류 문제에서 가장 많이 쓰이는 손실 함수입니다. 이 손실 함수는 모델의 예측이 실제 정답과 얼마나 차이가 나는지를 수치로 측정합니다. 크로스 엔트로피 손실의 원리를 이해하려면 '정보', '기대값', '엔트로피' 세 가지 개념을 먼저 알아야 합니다.

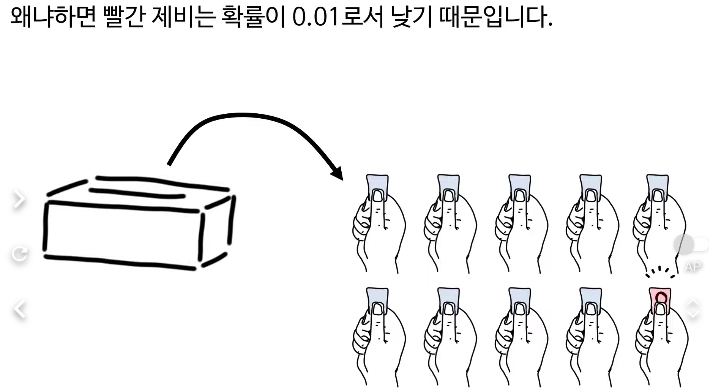
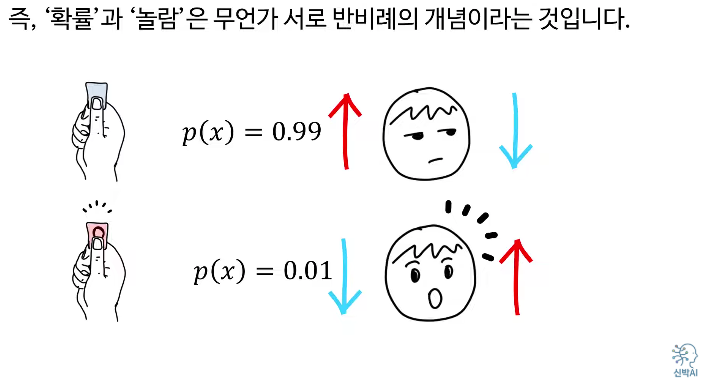
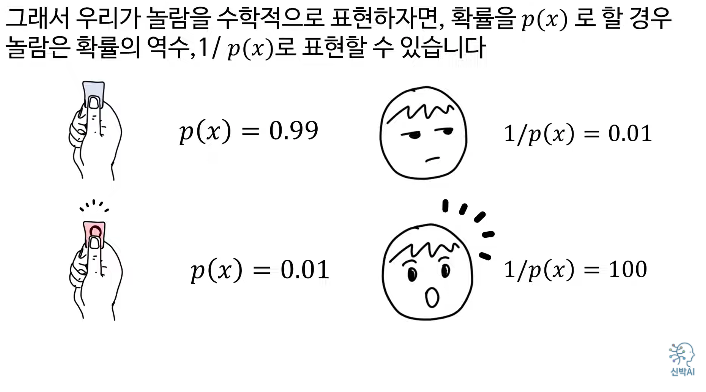
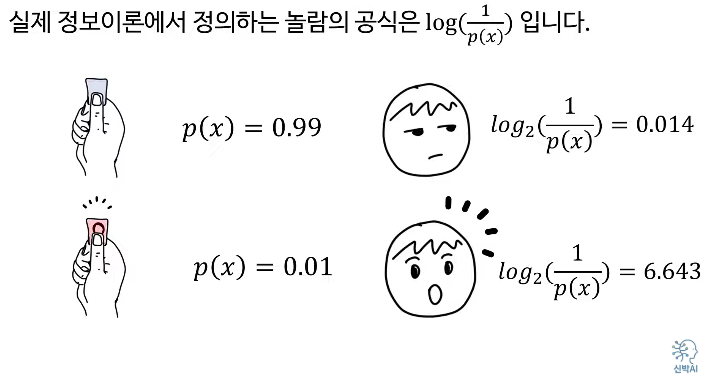
'놀람'은 상당히 주관적이고 심리적인 현상이기에 이 표현보다는 '정보'라는 단어를 쓴다.

이름이 어찌 되었든, 그 의미가 확률의 반비례 라는 것이 여기서는 중요하다.

x 대신 놀람도를 넣으면 엔트로피 공식이 된다.

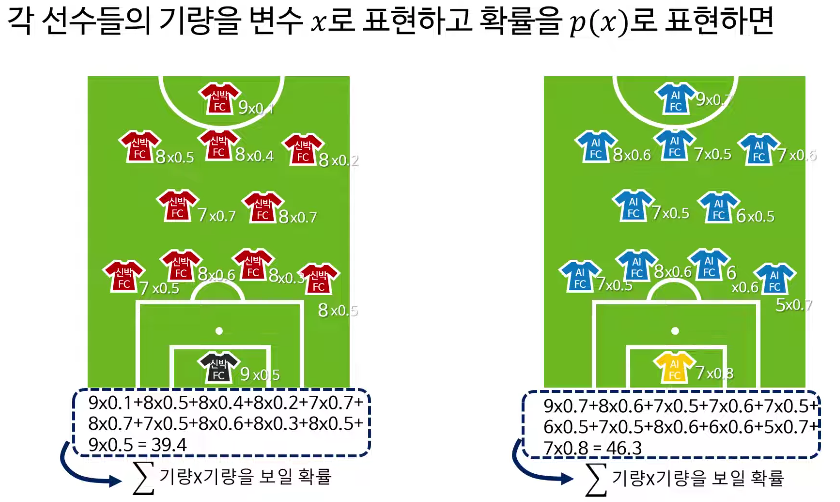
전력도 같고, 예상 기대값도 같다면, 엔트로피를 고려해 볼 수 있다.

왼쪽 팀 - 확률이 안정적(높거나 낮음)-> 낮은 수로 수렴 , 오른쪽 팀 - 놀랄 수 있다... 0.5인 절반에 가까울수록 -> 높은수로 수렴?

왼쪽 팀을 선택하는게 좋은 선택이다.

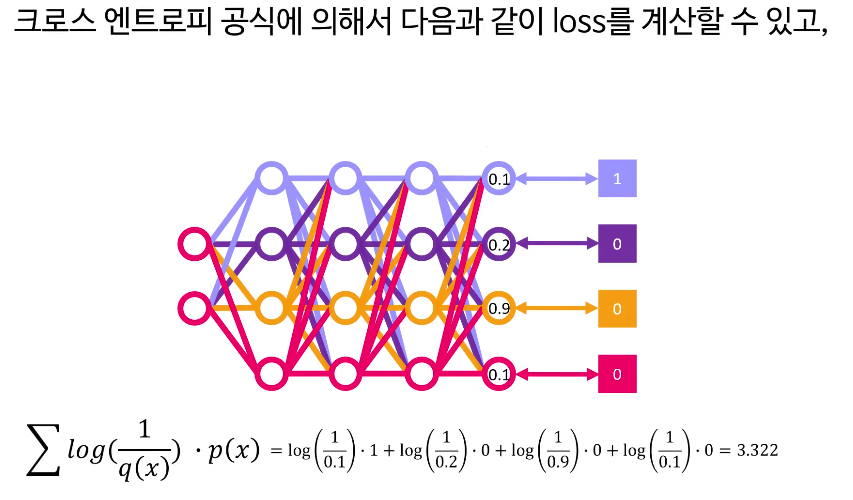
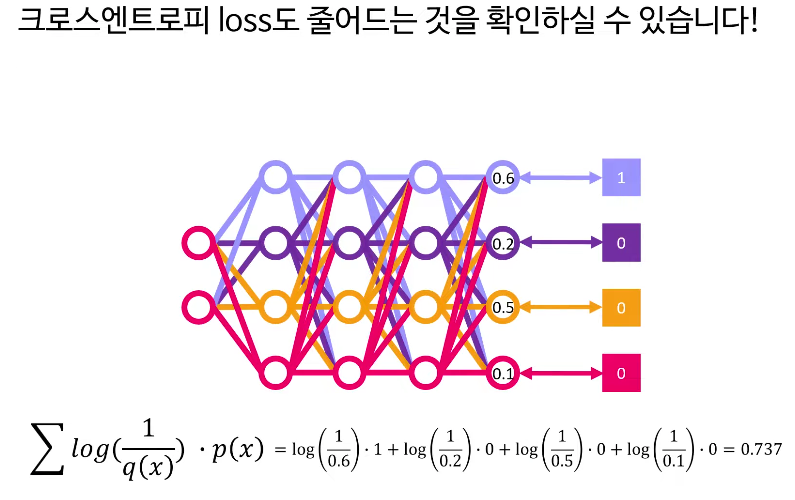
경사하강법과 역전파를 이용하여 이 loss가 작아지는 방향으로 신경망의 연결가중치들을 업데이트 하면된다.

업데이트 하고 나면, 신경망의 아웃풋이 다음과 같이 업데이트가 되고 실제값가 가까워진다면, 그에 따라

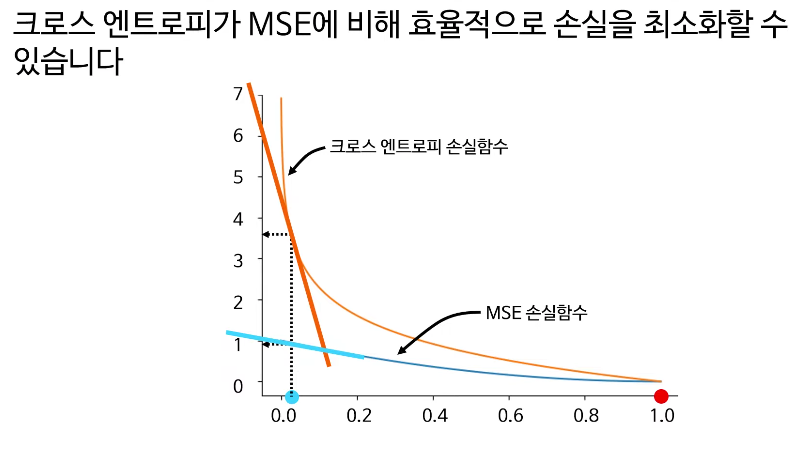
★★★★★ 크로스엔트로피가 MSE(Mean Square Error) 손실함수 보다 더 좋은 이유

MSE는 좋은 손실함수이고 직관적이고 쓰기 쉽다. 그러나 크로스 엔트포리가 손실을 더 잘보여준다.

실제값, 즉, Ground truth가 1 일때,

1에 가까우면 잘 예측

0에 가까오면 예측력이 떨어진다.

이 때,(0일때) 크로스엔트로피의 기울기도 훨씬 커서 효율적으로 손실을 최소화할 수 있다.

정보(Information) 공식

\[
I(x) = -\log P(x)
\]

기대값(Expected Value) 공식
\[
E[X] = \sum_x x \cdot P(x)
\]

엔트로피(Entropy) 공식
\[
H(P) = -\sum_x P(x) \log P(x)
\]

크로스 엔트로피(Cross Entropy) 공식
\[
H(P, Q) = -\sum_x P(x) \log Q(x)
\]

% 분류 신경망의 one-hot 정답 벡터를 기준으로 크로스 엔트로피 손실 함수

\[
\mathcal{L}(y, p) = -[y \log p + (1-y) \log (1-p)]
\]

정보란 무엇인가요?
어떤 일이 발생할 확률 P(x)P(x)가 높으면 그 사건이 일어나도 별로 놀랍지 않지만, 확률이 낮은 일이 발생하면 많이 놀라게 됩니다. 이 놀람의 정도(정보)는 수학적으로

\[정보=log⁡(1P(x))=−log⁡P(x)\text{정보} = \log\left(\frac{1}{P(x)}\right) = -\log P(x)정보=log(P(x)1)=−logP(x)

로 표현합니다.

기대값이란?
기대값은 어떤 값에 해당 확률을 곱해 모두 더한 것입니다. 예를 들어, 축구 경기에서 선수들이 기량을 발휘할 확률을 각각 곱하고 더하면 팀의 예상 승리값(기대값)을 구할 수 있습니다. 이를 수식으로 나타내면,

기대값=∑xx⋅P(x)\text{기대값} = \sum_x x \cdot P(x)

엔트로피란?
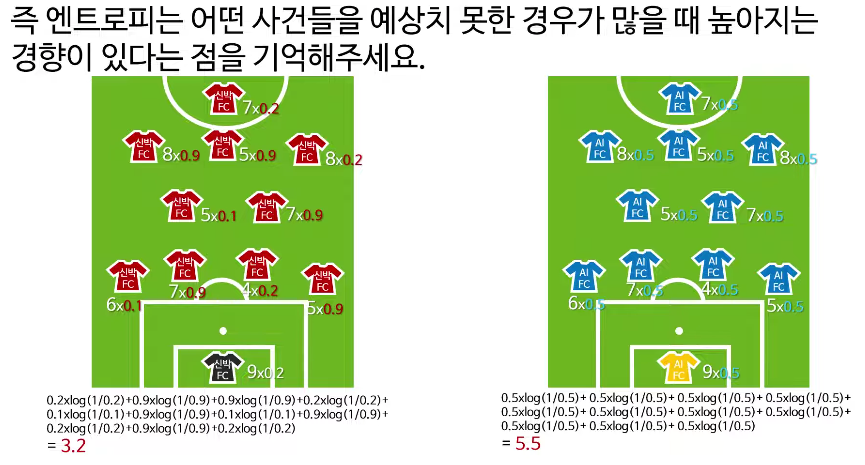
엔트로피는 놀람의 평균값, 즉 전체 사건의 불확실성입니다. 예측이 어렵고(확률이 0.5에 가까울 때) 엔트로피는 높으며, 확실한 경우(확률이 0이나 1일 때)에는 엔트로피가 낮습니다. 엔트로피 공식은 다음과 같습니다.

엔트로피=−∑xP(x)log⁡P(x)\text{엔트로피} = -\sum_x P(x) \log P(x)

크로스 엔트로피란?
크로스 엔트로피는 실제 정답 분포 P(x)P(x)와 모델 예측 분포 Q(x)Q(x)가 얼마나 다른지 측정합니다.

크로스 엔트로피=−∑xP(x)log⁡Q(x)\text{크로스 엔트로피} = -\sum_x P(x) \log Q(x)

즉, 실제 정답의 확률 값에 모델이 예측한 값의 놀람을 곱해 평균을 구하는 것입니다.

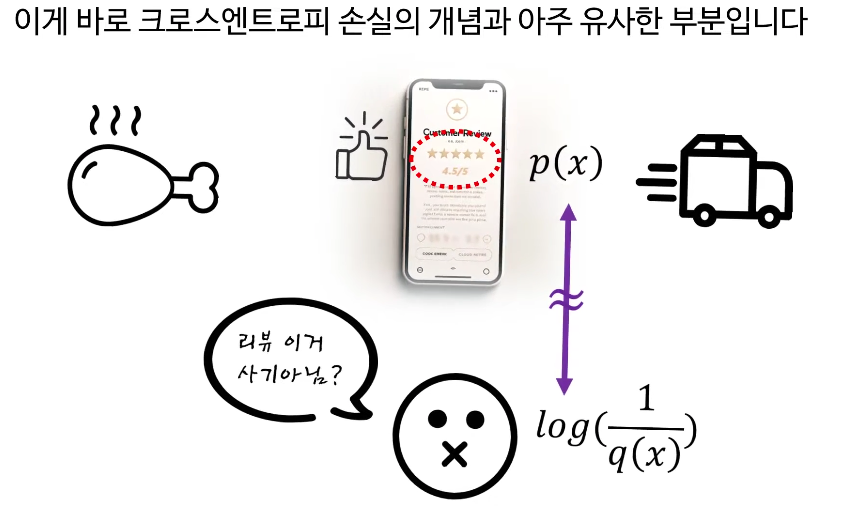
일상생활 예시(치킨집 리뷰):
치킨 리뷰 점수가 높은 집에서 배달을 시켰는데, 실제 맛이 기대에 못 미치면 실망하게 됩니다. 이처럼 실제 정답과 예측에 괴리가 있다면 '손실'이 생깁니다. 신경망 출력값과 실제 정답이 가까우면 크로스 엔트로피 손실이 작아지고, 멀면 손실이 커집니다.

크로스 엔트로피 vs MSE
분류 문제에서는 크로스 엔트로피가 MSE(평균제곱오차)보다 더 효과적입니다. 실제값과 예측값의 차이가 클수록 크로스 엔트로피가 더 크게 기울어져 빠르고 효율적으로 손실을 줄일 수 있습니다.

즉, 크로스 엔트로피 손실 함수는 분류 문제에서 신경망이 더 빠르고 정확하게 학습되도록 도와주는 핵심적인 도구입니다.
딥러닝을 학습한다면 꼭 익혀야 할 필수 개념입니다.

크로스 엔트로피(Cross Entropy)는 딥러닝과 머신러닝에서 분류 문제를 다룰 때 가장 널리 쓰이는 손실 함수 중 하나입니다. '크로스 엔트로피 손실'은 모델의 예측이 실제 정답과 얼마나 차이가 나는지를 수치로 표현해줍니다. 이 개념을 이해하려면 먼저 정보, 기대값, 엔트로피란 세 가지 기본 개념을 알 필요가 있습니다.

먼저, 정보란 어떤 사건이 발생했을 때의 '놀람'의 정도를 말합니다. 확률이 높을수록 해당 사건이 일어나도 별로 놀랍지 않지만, 확률이 낮은 일이 발생하면 큰 놀라움을 느끼게 됩니다. 수학적으로 정보는 log⁡(1P(x))\log(\frac{1}{P(x)})로 표현합니다. 여기서 P(x)P(x)는 사건 x가 일어날 확률입니다.

다음으로 기대값은 어떤 값을 실제로 얻을 확률을 곱해 모두 더한 것입니다. 예를 들어, 축구 경기에서 각 팀의 기량과 당일 컨디션에 확률을 곱해 종합하면 예상 승리값, 즉 기대값이 됩니다.

엔트로피는 놀람의 기대값이라고 생각하면 쉽습니다. 즉, 사건이 얼마나 예측하기 힘든지, 그 불확실성을 나타내는 지표입니다. 예측이 어려울수록(확률이 0.5에 가까울수록) 엔트로피는 높아지고, 매우 확실한 사건일수록(확률이 0이나 1에 가까울수록) 엔트로피는 낮아집니다.

이제 크로스 엔트로피로 넘어가겠습니다. 크로스 엔트로피는 실제 정답 분포와 모델이 예측한 분포의 차이를 측정합니다. 일상 예로 치킨집 리뷰 점수와 실제 맛이 다르다면 실망감을 느끼듯, 모델 예측과 정답이 다르면 불편함(손실)이 계산됩니다. 수식으로는 정답의 분포와 예측 분포를 비교해서 얼마나 차이가 큰지 계산하게 됩니다.

딥러닝에서 크로스 엔트로피 손실 함수는 예측값이 정답에 가까울수록 손실이 줄어들고, 멀어질수록 손실이 커집니다. 이를 이용해 경사하강법 등 최적화 과정을 거치며 모델 파라미터를 조정하게 되죠.

특히 분류 문제에서 크로스 엔트로피는 MSE(평균제곱오차)보다 기울기도 커서, 예측값이 정답과 멀수록 더 빠르게 손실을 줄이는 방향으로 학습이 이루어진다는 장점이 있습니다. 이 때문에 딥러닝 분류 문제에서는 사실상 표준처럼 사용됩니다.

결국 크로스 엔트로피는 "모델 예측이 얼마나 실제 정답과 다른지, 얼만큼 불확실한지"를 아주 효과적으로 수치화하여 딥러닝의 학습 기반이 되는 필수적인 개념입니다.