weekly-contest-222
leetcode.com/contest/weekly-contest-222
| 222 | 9692 | 4096 | 1594 | 664 | 247 | 42.26% | 16.45% | 6.85% | 2.55% | 12.58% |
My 2021 is ruined :(
TLE for both q2 and q3
1710. Maximum Units on a Truck
leetcode.com/problems/maximum-units-on-a-truck/
class Solution:
def maximumUnits(self, boxTypes: List[List[int]], truckSize: int) -> int:
boxTypes.sort(key=lambda x: -x[1])
max_units = 0
for n, units in boxTypes:
max_units += units * min(n, truckSize)
truckSize -= min(n, truckSize)
if truckSize <= 0:
break
return max_units1711. Count Good Meals
leetcode.com/problems/count-good-meals/
Note that the number of powers of 2 is at most 21 so this turns the problem to a classic find the number of pairs that sum to a certain value but for 21 values
You need to use something fasters than the NlogN approach since there is already the log of iterating over the powers so one idea is two pointers
class Solution:
def countPairs(self, ds: List[int]) -> int:
dp = defaultdict(int)
res = 0
for d in ds:
for i in range(22):
res += dp[2**i - d]
res %= (10**9 + 7)
dp[d] += 1
return res
1712. Ways to Split Array Into Three Subarrays
leetcode.com/problems/ways-to-split-array-into-three-subarrays/
Create a prefix array to efficiently find the sum of subarrays.
As we are dividing the array into three subarrays, there are two "walls". Iterate over the right wall positions and find where the left wall could be for each right wall position.
Use binary search to find the left-most position and right-most position the left wall could be.
Solution
Overview
The problem asks us to split the array into three parts such that the sum of the left part \leq≤ sum of the middle part \leq≤ the sum of the right part.

A brute force approach is to iterate over all possible locations of the first and second cut in the picture, which costs \mathcal{O}(N^{2})O(N2), given that NN is the length of nums.
However, with Binary Search, we can achieve \mathcal{O}(N\log N)O(NlogN).
Below, two approaches are introduced: Binary Search (Built-in) and Binary Search (Handmade). The first one calls the built-in API in the programming language for binary search, and in the second one, we write our own binary search implementation, in case that interviewers require so.
Approach 1: Binary Search (Built-in)
Intuition
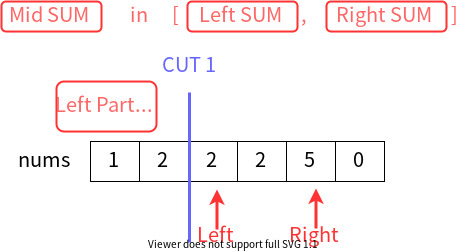
An important insight is that: the sum of the middle part must fall in the range of the sum of the left and right parts.
\text{LeftSum} \leq \text{MidSum} \leq \text{RightSum}LeftSum≤MidSum≤RightSum
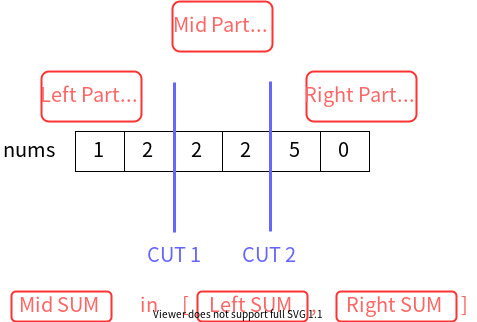
Also,
\text{LeftSum} + \text{MidSum} + \text{RightSum} = \text{TotalSum}LeftSum+MidSum+RightSum=TotalSum
We can easily calculate the \text{TotalSum}TotalSum by simple adding.
This means, once the \text{LeftSum}LeftSum is determined, the range of \text{MidSum}MidSum is also determined.
\text{LeftSum} \leq \text{MidSum} \leq \text{RightSum} = \text{TotalSum} - (\text{LeftSum} + \text{MidSum})LeftSum≤MidSum≤RightSum=TotalSum−(LeftSum+MidSum)
We can simplify the right part:
\text{MidSum} \leq \text{TotalSum} - (\text{LeftSum} + \text{MidSum}) = \text{TotalSum} - \text{LeftSum} - \text{MidSum}MidSum≤TotalSum−(LeftSum+MidSum)=TotalSum−LeftSum−MidSum
2 \cdot \text{MidSum} \leq \text{TotalSum} - \text{LeftSum}2⋅MidSum≤TotalSum−LeftSum
\text{MidSum} \leq \frac{\text{TotalSum} - \text{LeftSum}}{2}MidSum≤2TotalSum−LeftSum
Combine together, we have:
\text{LeftSum} \leq \text{MidSum} \leq \frac{\text{TotalSum} - \text{LeftSum}}{2}LeftSum≤MidSum≤2TotalSum−LeftSum
This give us the range of \text{MidSum}MidSum once \text{LeftSum}LeftSum is determined.
Since all numbers in nums are natural number, we can use Binary Search to find out the minimal possible index and the maximum possible index of \text{MidSum}MidSum.
In conclusion, we can iterate over the first cut to determine \text{LeftSum}LeftSum, and use binary search to find all possible locations of the second cut.
To speed up the calculation of sum, Prefix Sum can help us.
Algorithm
Step 1: Initialize a prefix sum list presum, where presum[i+1] store the sum from nums[0] to nums[i], inclusive.
Step 2: Iterate over nums. For each element nums[i]:
- Cut nums into (nums[0],...,nums[i]) | (nums[i+1], nums[i+2], ...).
- Calculate the sum of (nums[0],..., nums[i]) with presum. Mark as leftSum.
- Calculate the sum of (nums[i+1], nums[i+2], ...) with presum. Mark as remain.
- Then we need to cut the remaining part into two pieces, and the sum of the middle piece should be between leftSum and remain/2.
- Binary search the minimal first such that nums[i+1] + ... + nums[first] >= leftSum.
- Binary search the maximum last such that nums[i+1] + ... + nums[second] <= remain/2.
- Add last - first + 1 to the final result.
Step 3: Return the final result.
In this approach, we use built-in functions to perform binary searches. In the next approach, we will implement our own binary search functions.
Warning!: Unfortunately, Java does not have a nice built-in binary search to find out the upper bound of the index of the second cut (such as upper_bound in C++).
In this case, we have to use a TreeMap to mimic the function. If you are not familiar with TreeMap, this trick is not recommended since implementing your own binary search functions would be usually faster.
Challenge: Can you implement the code yourself without seeing our implementations?
Implementation
class Solution:
def waysToSplit(self, nums: List[int]) -> int:
n = len(nums)
MOD = 10**9+7
presum = [0]*(n+1)
for i in range(n):
presum[i+1] = presum[i]+nums[i]
result = 0
for i in range(n-2):
leftSum = presum[i+1]
remain = presum[n] - leftSum
if remain < leftSum * 2:
break
first = bisect.bisect_left(presum, leftSum + leftSum, i+2, n)
last = bisect.bisect_right(presum, leftSum + remain//2, i+2, n) - 1
result += max(last-first+1, 0)
return result % MOD
Complexity Analysis
Let NN be the length of nums.
-
Time Complexity: \mathcal{O}(N\log N)O(NlogN), since we need to iterate over nums and for each element, we perform binary search twice which costs \mathcal{O}(\log N)O(logN).
-
Space Complexity: \mathcal{O}(N)O(N), since we need \mathcal{O}(N)O(N) to store presum.
Approach 2: Binary Search (Handmade)
Intuition
Some interviewers may not be satisfied with the built-in functions, and require us to implement our own functions. In this case, we have no choice but to write one.
In Approach 1, we get a range of \text{MidSum}MidSum:
\text{LeftSum} \leq \text{MidSum} \leq \frac{\text{TotalSum} - \text{LeftSum}}{2}LeftSum≤MidSum≤2TotalSum−LeftSum
Now we need two functions, one searching the lower bound, and one searching the upper bound.
Let's consider the lower bound first. Precisely, we need a function to find out the minimal j such that nums[i+1] + ... + nums[j] >= LeftSum.
The common structure of a binary search is as below (In pseudo-code):
# in nums[i+1:n-1] find the min j s.t. # nums[i+1]+...+nums[j] >= target Initialize left, right pointing the boundary while left < right: mid = (left+right)/2 calculate something according to mid if the requirement satisfied: right = mid else: left = mid+1 return left
The difficulty of binary search is that a lot of detail can be changed in the structure above. For example, one can replace mid = (left+right)//2 with mid = (left+right)/2 + 1, or change right = mid into right = mid + 1.
However, different combinations can have different performances and different results, and some combinations might even go into an infinite loop. One should be careful when dealing with those details.
It is recommended to check the discussion and the solution of the LeetCode problem Binary Search for those details.
One recommendation is to remember one template and derive other possible variants from that template.
Now we will start from the template from the pseudo-code above.
left and right should be initialized to the boundary of possible answers. Say we cut nums into (nums[0],...,nums[i]) | (nums[i+1], nums[i+2], ...), then left=i+1 and right=n-2.
Why right is not the last index n-1? Because we need to leave at least one element in \text{RightSum}RightSum.
Then we need to decide the requirement. From the requirement, we can figure out what calculation we need to do with mid. In our case, the requirement is nums[i+1] + ... + nums[j] >= LeftSum. To calculate this requirement, we need to use the prefix sum.
To sum up, there is our final pseudo-code:
# in nums[i+1:n-1] find the min j s.t. # nums[i+1]+...+nums[j] >= target left = i+1 right = n-2 while left < right: mid = (left+right)/2 calculate (nums[i+1] + ... + nums[j]) and LeftSum if nums[i+1] + ... + nums[j] >= LeftSum: right = mid else: left = mid+1 return left
Cool. The last thing is to confirm there is no infinite loop. The most likely loop case is when left and right is very close, say right = left + 1. In this case mid = (left+right)/2 = left. If left and right remain unchanged, then we go into a loop. In our code, either right = mid (which changes right) or left = mid + 1 (which changes left), which means, there is no loop!
If there is some loop, you might want to change something like mid = (left+right)/2 + 1 or right = mid - 1, which prevent left and right remaining unchanged.
Now we have a workable code. The upper bound case is similar but requires some changes on the template.
Algorithm
Step 1: Implement two binary search functions. The first one can search the minimal j such that nums[i+1] + ... + nums[j] >= target. The second one can search the maximum j such that nums[i+1] + ... + nums[j] <= target.
Step 2: Initialize a prefix sum list presum, where presum[i+1] store the sum from nums[0] to nums[i], inclusive.
Step 3: Iterate over nums. For each element nums[i]:
- Cut nums into (nums[0],...,nums[i]) | (nums[i+1], nums[i+2], ...).
- Calculate the sum of (nums[0],..., nums[i]) with presum. Mark as leftSum.
- Calculate the sum of (nums[i+1], nums[i+2], ...) with presum. Mark as remain.
- Then we need to cut the remaining part into two pieces, and the sum of the middle piece should be between leftSum and remain/2.
- Binary search the minimal first such that nums[i+1] + ... + nums[first] >= leftSum with the implemented function.
- Binary search the maximum last such that nums[i+1] + ... + nums[second] <= remain/2 with the implemented function.
- Add last - first + 1 to the final result.
Step 4: Return the final result.
Challenge: Can you implement the code yourself without seeing our implementations?
Implementation
Note: In the Python implementation above, we use camelCase to name the function. This is to keep consistent with the given method name waysToSplit, which is also camelCase. In real practice, snake_case is preferred according to PEP 8.
Complexity Analysis
Let NN be the length of nums.
-
Time Complexity: \mathcal{O}(N\log N)O(NlogN), since we need to iterate over nums and for each element, we perform binary search twice which costs \mathcal{O}(\log N)O(logN).
-
Space Complexity: \mathcal{O}(N)O(N), since we need \mathcal{O}(N)O(N) to store presum.
1713. Minimum Operations to Make a Subsequence
leetcode.com/problems/minimum-operations-to-make-a-subsequence/
The problem can be reduced to computing Longest Common Subsequence between both arrays.
Since one of the arrays has distinct elements, we can consider that these elements describe an arrangement of numbers, and we can replace each element in the other array with the index it appeared at in the first array.
Then the problem is converted to finding Longest Increasing Subsequence in the second array, which can be done in O(n log n).





