1640. Check Array Formation Through Concatenation

leetcode.com/problems/check-array-formation-through-concatenation/

 

공간이 중요할때는 바이너리서치

시간이 중요할때는 해쉬맵 사용

 

 

You are given an array of distinct integers arr and an array of integer arrays pieces, where the integers in pieces are distinct. Your goal is to form arr by concatenating the arrays in pieces in any order. However, you are not allowed to reorder the integers in each array pieces[i].

Return true if it is possible to form the array arr from pieces. Otherwise, return false.

 

Example 1:

Input: arr = [85], pieces = [[85]] Output: true

Example 2:

Input: arr = [15,88], pieces = [[88],[15]] Output: true Explanation: Concatenate [15] then [88]

Example 3:

Input: arr = [49,18,16], pieces = [[16,18,49]] Output: false Explanation: Even though the numbers match, we cannot reorder pieces[0].

Example 4:

Input: arr = [91,4,64,78], pieces = [[78],[4,64],[91]] Output: true Explanation: Concatenate [91] then [4,64] then [78]

Example 5:

Input: arr = [1,3,5,7], pieces = [[2,4,6,8]] Output: false

 

Constraints:

• 1 <= pieces.length <= arr.length <= 100
• sum(pieces[i].length) == arr.length
• 1 <= pieces[i].length <= arr.length
• 1 <= arr[i], pieces[i][j] <= 100
• The integers in arr are distinct.
• The integers in pieces are distinct (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct).

 

 

 

Solution

---

Overview

Once you noticed that the integers in pieces are distinct, the problem becomes simple. We can use several different methods to match the target array without worrying about duplicates.

Below, we will discuss three methods: One by One, Binary Search, and HashMap. We recommend the third approach since it's the fastest one and easy to implement.

---

Approach 1: One by One

Intuition

Let's start with the most natural approach.

For a given array arr, we need to find all corresponding integers from pieces for all integers arr[i].

Let's start from left to right. Consider the leftmost element arr[0].

We need to find a piece containing arr[0]. Of course, arr[0] should be at the start of the target piece.

Now, we have an essential characteristic of our target piece: it should start with arr[0].

OK. With this characteristic, we can iterate over pieces to find our target piece. Since there is no duplicate integer in pieces, we will have at most one eligible piece.

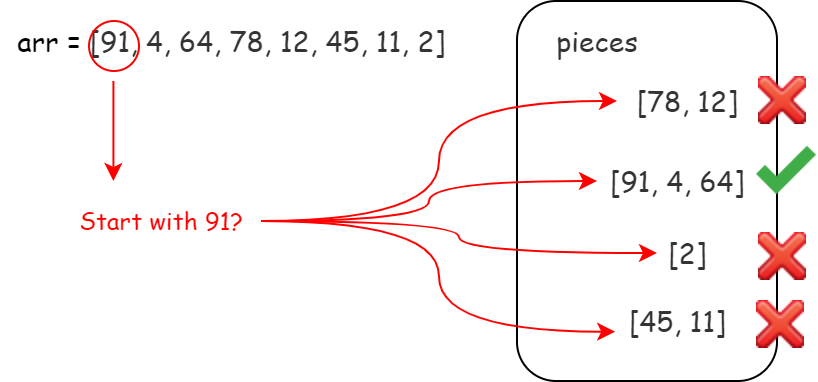
If we can not find any, return false. If we found one, then the piece found should be the same as the beginning of arr.

We should check whether each integer in the piece matches the beginning of arr.

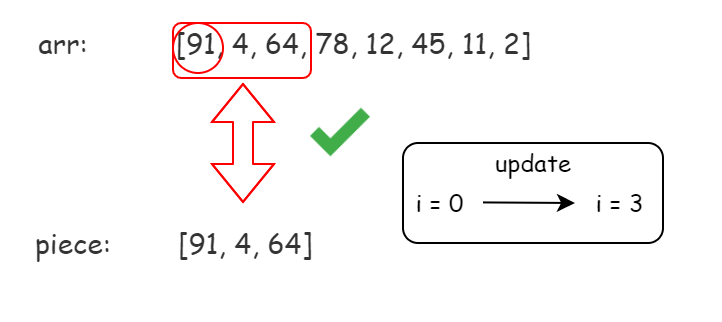
If not matched, we should return false. If all matched, then we found the first piece!

Now, we move the i to the next unmatched index and repeat the operation above until we reach the end of arr.

Also, because we have constraint sum(pieces[i].length) == arr.length and no repeated number in arr or in pieces, if we ensure each integer in arr is matched, then each piece in pieces is matched.

In this case, we successfully found whether we can concatenate pieces in any order to form arr.

Algorithm

Step 1: Initialize an index i to record the current matching index in arr.

Step 2: Iterate over pieces to find the piece starting with arr[i]. Return false if no match.

Step 3: Use the matched piece to match arr's sublist starting from i with the same length. Return false if any integer is different.

Step 4: Increment the index i.

Step 5: Repeat until i reach the end of arr. Return true.

Challenge: Can you implement the code yourself without seeing our implementations?

Implementation

class Solution:
    def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:
        n = len(arr)
        i = 0
        while i < n:
            for p in pieces:
                if p[0] == arr[i]:
                    break
            else:
                return False
                
            for x in p:
                if x != arr[i]:
                    return False
                i += 1
        return True

for:

else:

 

 

Complexity Analysis

Let NN be the length of arr. In the worst case, the size of pieces is \mathcal{O}(N)O(N).

• Time Complexity: \mathcal{O}(N^2)O(N2). The time to find the next piece is \mathcal{O}(N)O(N), and we need to find \mathcal{O}(N)O(N) pieces at most.

• Space Complexity: \mathcal{O}(1)O(1), since no additional data structure is allocated.

---

Approach 2: Binary Search

Intuition

The one by one search in Approach 1 is expensive. Can we make it faster?

Yes. We can sort the pieces according to their first element and use the Binary Search to find out the next target piece.

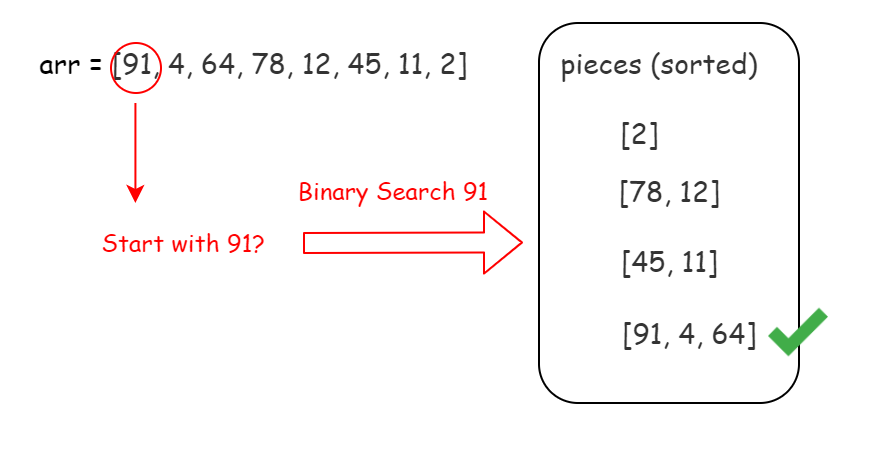
Algorithm

Step 1: Initial an index i to record the current matching index in arr.

Step 2: Use binary search to find the piece starting with arr[i]. Return false if no match.

Step 3: Use the matched piece to match arr's sublist starting from i with the same length. Return false if any integer is different.

Step 4: Increment the index i.

Step 5: Repeat until i reach the end of arr. Return true.

Challenge: Can you implement the code yourself without seeing our implementations?

Implementation

class Solution:
    def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:
        n = len(arr)
        p_len = len(pieces)
        pieces.sort()
        
        i = 0
        while i < n:
            left = 0
            right = p_len - 1
            found = -1
            
            while left <= right:
                mid = (left + right) // 2
                if pieces[mid][0] == arr[i]:
                    found = mid
                    break
                elif pieces[mid][0] > arr[i]:
                    right = mid - 1
                else:
                    left = mid + 1
            if found == -1:
                return False
            target_piece = pieces[found]
            for x in target_piece:
                if x != arr[i]:
                    return False
                i += 1
        return True

Complexity Analysis

Let NN be the length of arr. In the worst case, the size of pieces is \mathcal{O}(N)O(N).

• Time Complexity: \mathcal{O}(N\log(N))O(Nlog(N)). The time to find next piece using Binary Search is \mathcal{O}(\log(N))O(log(N)), and we need to find \mathcal{O}(N)O(N) pieces at most.

• Space Complexity: \mathcal{O}(1)O(1), since no additional data structure is allocated.

---

Approach 3: HashMap

Intuition

We are still not satisfied with the binary search in Approach 2. Can we make it faster?

Yes. We can store the pieces according to their first element in a hashmap.

In this case, we can get our target piece in \mathcal{O}(1)O(1).

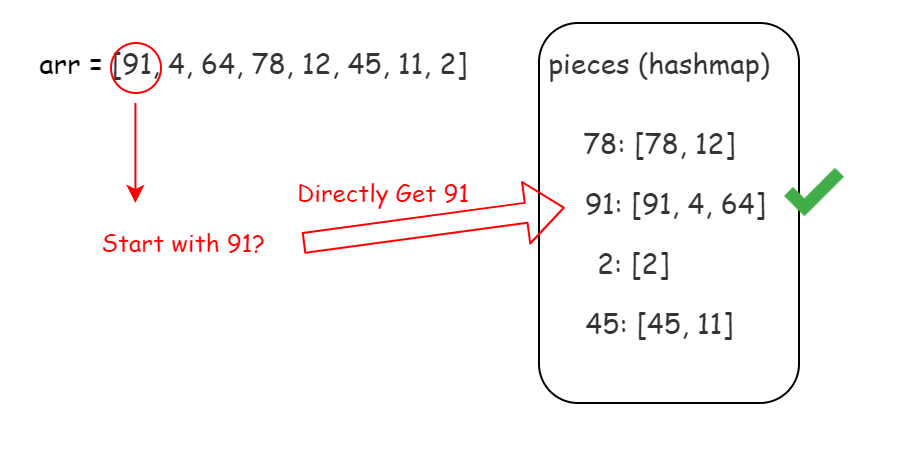
Algorithm

Step 1: Initialize a hashmap mapping to record piece's first integer and the whole piece mapping.

Step 2: Initialize an index i to record the current matching index in arr.

Step 3: Find the piece starting with arr[i] in mapping. Return false if no match.

Step 4: Use the matched piece to match arr's sublist starting from i with the same length. Return false if any integer is different.

Step 5: Increment the index i.

Step 6: Repeat until i reach the end of arr. Return true.

Challenge: Can you implement the code yourself without seeing our implementations?

Implementation

class Solution:
    def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:
        n = len(arr)
        mapping = {p[0]: p for p in pieces}
        
        i = 0
        while i < n:
            if arr[i] not in mapping:
                return False
            target_piece = mapping[arr[i]]
            for x in target_piece:
                if x != arr[i]:
                    return False
                i += 1
                
        return True

mapping = {p[0]: p for p in pieces}

 

 

Complexity Analysis

Let NN be the length of arr. In the worst case, the size of pieces is \mathcal{O}(N)O(N).

• Time Complexity: \mathcal{O}(N)O(N). The time to find next piece is \mathcal{O}(1)O(1), and we need to find \mathcal{O}(N)O(N) pieces at most.

• Space Complexity: \mathcal{O}(N)O(N), since we store a hashmap with \mathcal{O}(N)O(N) elements at most.