LCA ( Lowest Common Ancestor )

리트코드에서 공통조상찾기 문제를 풀어봅시다.

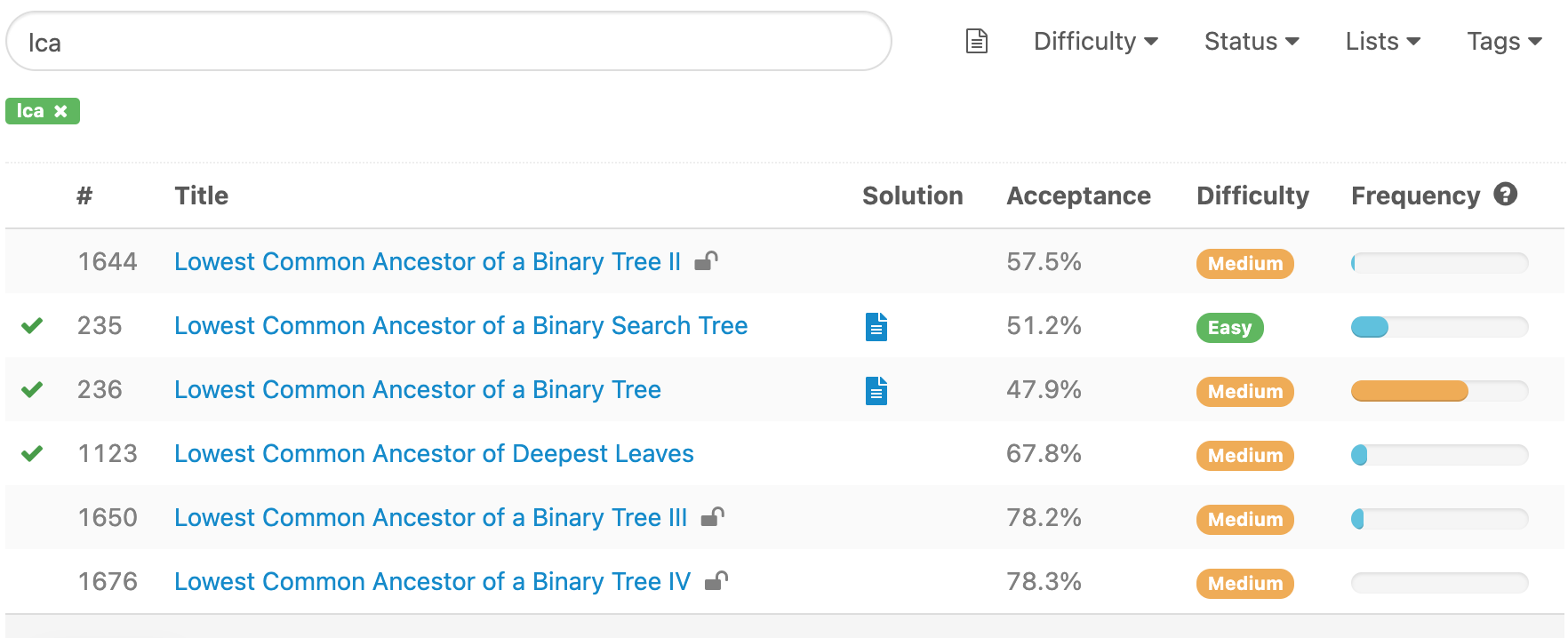
235. Lowest Common Ancestor of a Binary Search Tree

leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/

진정한 LCA 문제라기 보다는, BST의 특성을 이용해 값을 기준으로 부모노드의 위치를 찾아가는 문제.

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        parent_val = root.val
        p_val = p.val
        q_val = q.val
        
        if p_val > parent_val and q_val > parent_val:
            return self.lowestCommonAncestor(root.right, p, q)
        elif p_val < parent_val and q_val < parent_val:
            return self.lowestCommonAncestor(root.left, p, q)
        else:
            return root

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        p_val = p.val
        q_val = q.val
        node = root
        while node:
            parent_val = node.val
            if p_val > parent_val and q_val > parent_val:
                node = node.right
            elif p_val < parent_val and q_val < parent_val:
                node = node.left
            else:
                return node

236. Lowest Common Ancestor of a Binary Tree

leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree/

3개 다 O(N) O(N) 이긴 하지만..

Approach 1: Recursive Approach

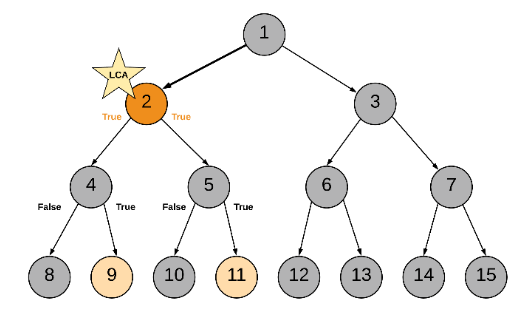
class Solution:
    ans = 0
    
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        def recurse_tree(current_node):
            if not current_node:
                return False
            left = recurse_tree(current_node.left)
            right = recurse_tree(current_node.right)
            mid = current_node == p or current_node == q
            if mid + left + right >= 2:
                self.ans = current_node
            return mid or left or right
        recurse_tree(root)
        return self.ans

Approach 2: Iterative using parent pointers

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        stack = [root]
        parent = {root: None}
        while p not in parent or q not in parent:
            node = stack.pop()
            if node.left:
                parent[node.left] = node
                stack.append(node.left)
            if node.right:
                parent[node.right] = node
                stack.append(node.right)
        ancestors = set()
        while p:
            ancestors.add(p)
            p = parent[p]
        while q not in ancestors:
            q = parent[q]
        return q

Approach 3: Iterative without parent pointers

In the previous approach, we come across the LCA during the backtracking process. We can get rid of the backtracking process itself. In this approach we always have a pointer to the probable LCA and the moment we find both the nodes we return the pointer as the answer.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    BOTH_PENDING = 2
    LEFT_DONE = 1
    BOTH_DONE = 0
    
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        stack = [(root, Solution.BOTH_PENDING)]
        one_node_found = False
        LCA_index = -1
        
        while stack:
            parent_node, parent_state = stack[-1]
            
            if parent_state != Solution.BOTH_DONE:
                if parent_state == Solution.BOTH_PENDING:
                    if parent_node == p or parent_node == q:
                        if one_node_found:
                            return stack[LCA_index][0]
                        else:
                            one_node_found = True
                            LCA_index = len(stack) - 1
                    child_node = parent_node.left
                else:
                    child_node = parent_node.right
                stack.pop()
                stack.append((parent_node, parent_state - 1))

                if child_node:
                    stack.append((child_node, Solution.BOTH_PENDING))
            else:
                if one_node_found and LCA_index == len(stack) - 1:
                    LCA_index -= 1
                stack.pop()
        return None

1123. Lowest Common Ancestor of Deepest Leaves

leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def lcaDeepestLeaves(self, root: TreeNode) -> TreeNode:
        
        def dfs(root: TreeNode) -> TreeNode:
            if not root:
                return (0, None)

            h1, lca1 = dfs(root.left)
            h2, lca2 = dfs(root.right)

            if h1 > h2: return h1+1, lca1
            if h1 < h2: return h2+1, lca2
            return h1 + 1, root
        
        return dfs(root)[1]

leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-ii/

leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-iii/

leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-iv/

leetcode.com/problems/smallest-common-region/