1457. Pseudo-Palindromic Paths in a Binary Tree / 129. Sum Root to Leaf Numbers

1457. Pseudo-Palindromic Paths in a Binary Tree

leetcode.com/problems/pseudo-palindromic-paths-in-a-binary-tree/

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

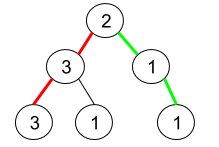
Input: root = [2,3,1,3,1,null,1] Output: 2 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

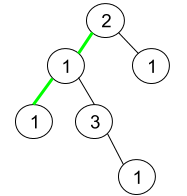
Input: root = [2,1,1,1,3,null,null,null,null,null,1] Output: 1 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

Input: root = [9] Output: 1

Constraints:

The given binary tree will have between 1 and 10^5 nodes.
Node values are digits from 1 to 9.

Solution

Overview

Two subproblems

The problem consists of two subproblems:

Traverse the tree to build all root-to-leaf paths.
For each root-to-leaf path, check if it's a pseudo-palindromic path or not.

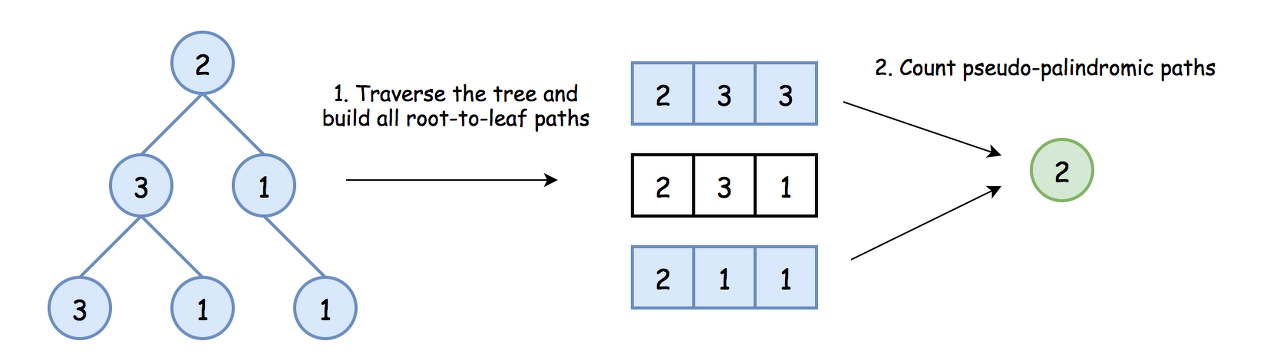
How to traverse the tree to build all root-to-leaf paths

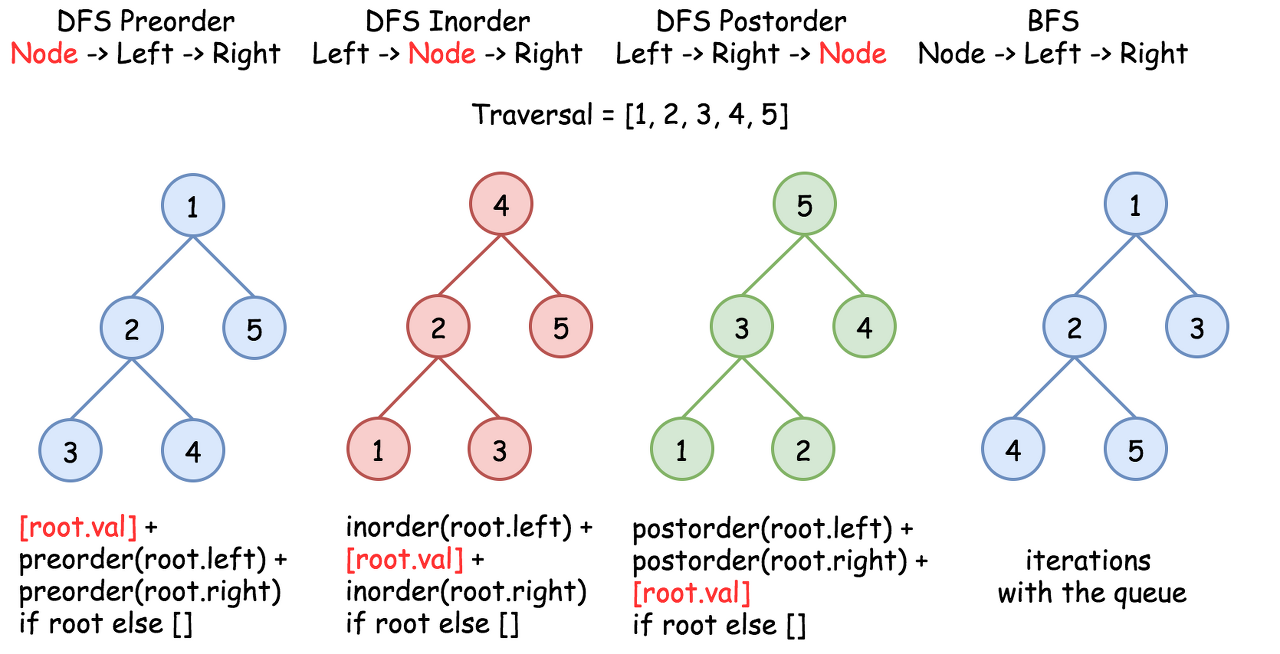
There are three DFS ways to traverse the tree: preorder, postorder and inorder. Please check two minutes picture explanation if you don't remember them quite well: here is Python version and here is Java version.

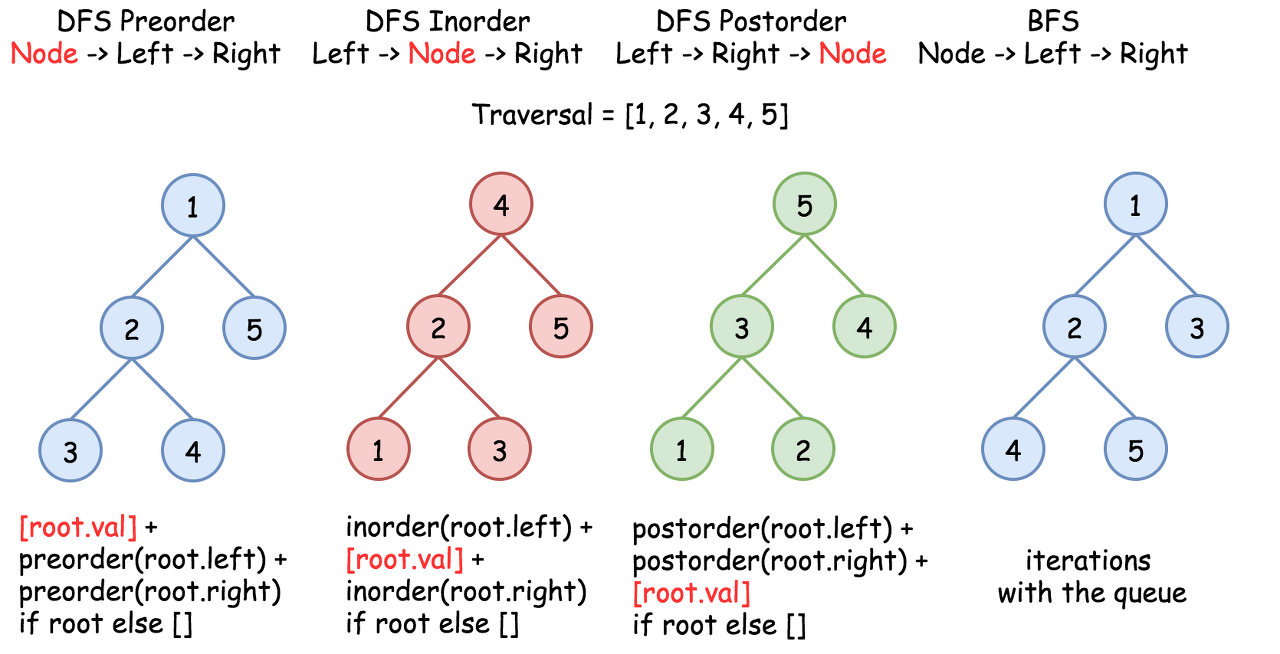
Figure 2. The nodes are enumerated in the order of visit. To compare different DFS strategies, follow 1-2-3-4-5 direction.

Root-to-leaf traversal is so-called DFS preorder traversal. To implement it, one has to follow the straightforward strategy Root->Left->Right.

There are three ways to implement preorder traversal: iterative, recursive, and Morris. Here we're going to implement the first two.

Iterative and recursive approaches here do the job in one pass, but they both need up to \mathcal{O}(H) space to keep the stack, where H is a tree height.

How to check if the path is pseudo-palindromic or not

It's quite evident that the path is pseudo-palindromic, if it has at most one digit with an odd frequency.

How to check that?

The straightforward way is to save each root-to-leaf path into a list and then to check each digit for parity.

def check_palindrom(nums):
    is_palindrom = 0

    for i in range(1, 10):
        if nums.count(i) % 2 == 1:
            is_palindrom += 1
            if is_palindrom > 1:
                return False

    return True

This method requires to keep each root-to-leaf path, and that becomes space-consuming for the large trees. To save the space, let's compute the parity on-the-fly using bitwise operators.

The idea is to keep the frequency of digit 1 in the first bit, 2 in the second bit, etc: path ^= (1 << node.val).

Left shift operator is used to define the bit, and XOR operator - to compute the digit frequency.

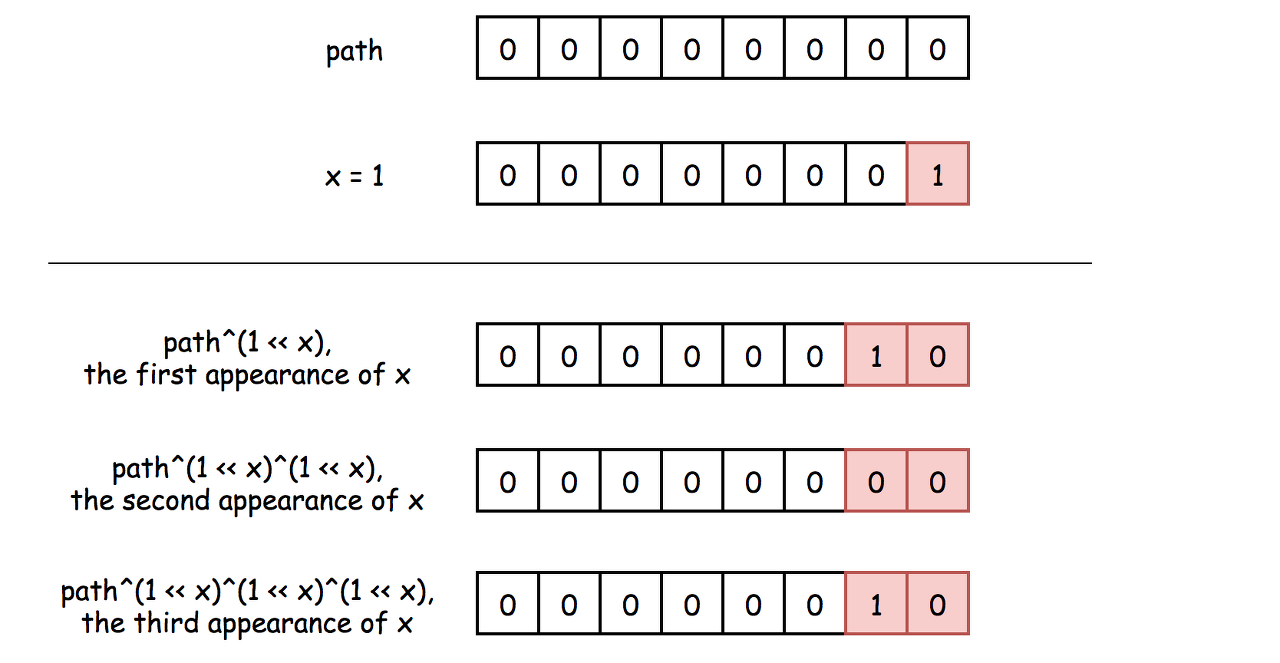
Figure 3. XOR of zero and a bit results in that bit. XOR of two equal bits (even if they are zeros) results in a zero. Hence, one could see the bit in a path only if it appears odd number of times.

# compute occurences of each digit 
# in the corresponding bit
path = path ^ (1 << node.val)

Now, to ensure that at most one digit has an odd frequency, one has to check that path is a power of two, i.e., at most one bit is set to one. That could be done by turning off (= setting to 0) the rightmost 1-bit: path & (path - 1) == 0. You might want to check the article Power of Two for the detailed explanation of this bitwise trick.

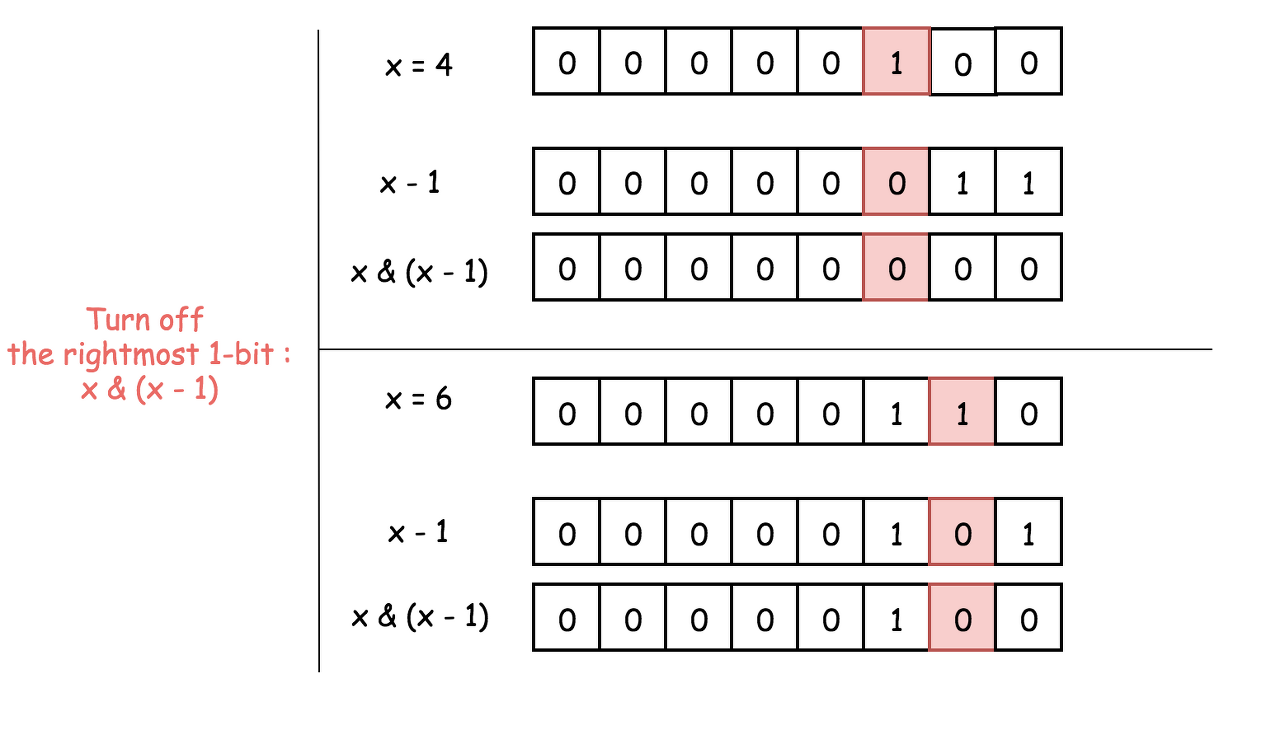
Figure 4. x & (x - 1) is a way to set the rightmost 1-bit to zero, i.e., x & (x - 1) == 0 for the power of two. To subtract 1 means to change the rightmost 1-bit to 0 and to set all the lower bits to 1. Now AND operator: the rightmost 1-bit will be turned off because 1 & 0 = 0, and all the lower bits as well.

# if it's a leaf, 
# check that at most one digit has an odd frequency
if path & (path - 1) == 0:
    count += 1

Approach 1: Iterative Preorder Traversal.

Intuition

1 / 9

Here we implement standard iterative preorder traversal with the stack:

Initialize the counter to zero.
Push root into stack.
While stack is not empty:
- Pop out a node from the stack and update the current number.
- If the node is a leaf, update the root-to-leaf path, check it for being pseudo-palindromic, and update the count.
- Push right and left child nodes into stack.
Return count.

Implementation

Note, that Javadocs recommends to use ArrayDeque, and not Stack as a stack implementation.

class Solution:
    def pseudoPalindromicPaths (self, root: TreeNode) -> int:
        count = 0
        
        stack = [(root, 0) ]
        while stack:
            node, path = stack.pop()
            if node is not None:
                # compute occurences of each digit 
                # in the corresponding register
                path = path ^ (1 << node.val)
                # if it's a leaf, check if the path is pseudo-palindromic
                if node.left is None and node.right is None:
                    # check if at most one digit has an odd frequency
                    if path & (path - 1) == 0:
                        count += 1
                else:
                    stack.append((node.right, path))
                    stack.append((node.left, path))
        
        return count

Complexity Analysis

Time complexity: \mathcal{O}(N) since one has to visit each node, where N is a number of nodes.
Space complexity: up to \mathcal{O}(H) to keep the stack, where H is a tree height.

Approach 2: Recursive Preorder Traversal.

Iterative approach 1 could be converted into a recursive one.

Recursive preorder traversal is extremely simple: follow Root->Left->Right direction, i.e., do all the business with the node (i.e., update the current path and the counter), and then do the recursive calls for the left and right child nodes.

P.S. Here is the difference between preorder and the other DFS recursive traversals.

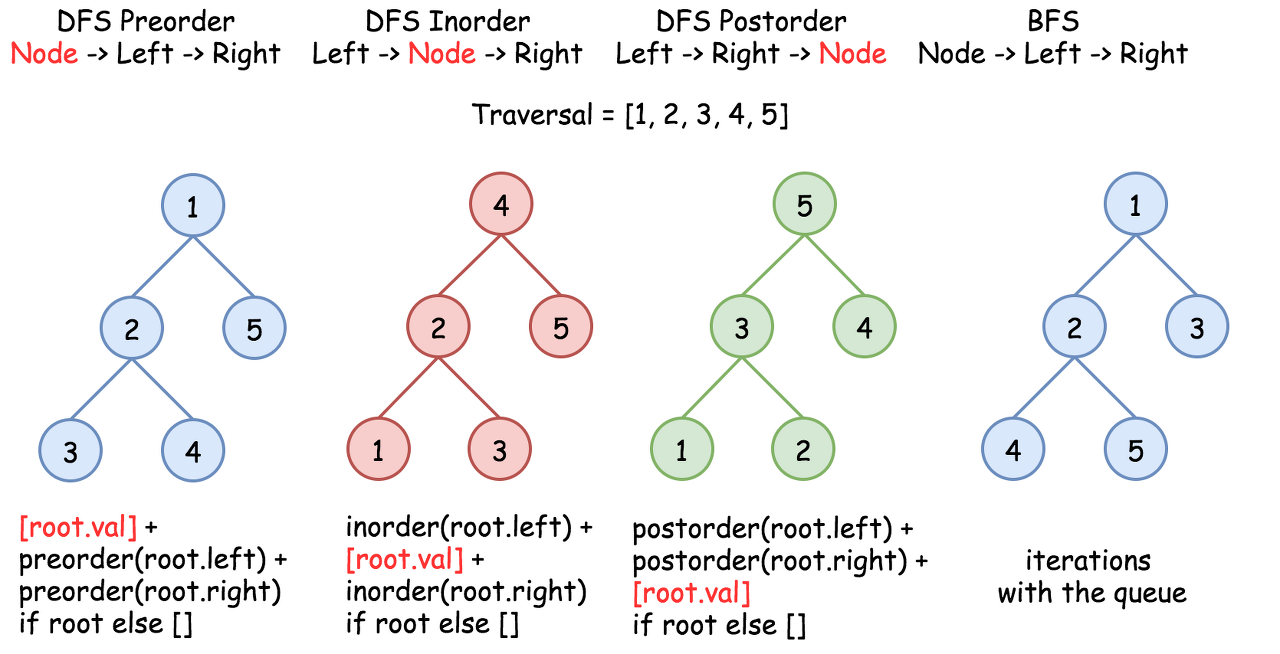
Figure 5. The nodes are enumerated in the order of visit. To compare different DFS strategies, follow 1-2-3-4-5 direction.

Implementation

class Solution:
    def pseudoPalindromicPaths (self, root: TreeNode) -> int:
        def preorder(node, path):
            nonlocal count
            if node:
                # compute occurences of each digit 
                # in the corresponding register
                path = path ^ (1 << node.val)
                # if it's a leaf, check if the path is pseudo-palindromic
                if node.left is None and node.right is None:
                    # check if at most one digit has an odd frequency
                    if path & (path - 1) == 0:
                        count += 1
                else:                    
                    preorder(node.left, path)
                    preorder(node.right, path) 
        
        count = 0
        preorder(root, 0)
        return count

Complexity Analysis

Time complexity: \mathcal{O}(N) since one has to visit each node, check if at most one digit has an odd frequency.
Space complexity: up to \mathcal{O}(H) to keep the recursion stack, where H is a tree height.

129. Sum Root to Leaf Numbers

leetcode.com/problems/sum-root-to-leaf-numbers/

Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.

An example is the root-to-leaf path 1->2->3 which represents the number 123.

Find the total sum of all root-to-leaf numbers.

Note: A leaf is a node with no children.

Example:

Input: [1,2,3] 1 / \ 2 3 Output: 25 Explanation: The root-to-leaf path 1->2 represents the number 12. The root-to-leaf path 1->3 represents the number 13. Therefore, sum = 12 + 13 = 25.

Example 2:

Input: [4,9,0,5,1] 4 / \ 9 0 / \ 5 1 Output: 1026 Explanation: The root-to-leaf path 4->9->5 represents the number 495. The root-to-leaf path 4->9->1 represents the number 491. The root-to-leaf path 4->0 represents the number 40. Therefore, sum = 495 + 491 + 40 = 1026.

Solution

Overview

Prerequisites

There are three DFS ways to traverse the tree: preorder, postorder and inorder. Please check two minutes picture explanation, if you don't remember them quite well: here is Python version and here is Java version.

Optimal Strategy to Solve the Problem

Root-to-left traversal is so-called DFS preorder traversal. To implement it, one has to follow straightforward strategy Root->Left->Right.

Since one has to visit all nodes, the best possible time complexity here is linear. Hence all interest here is to improve the space complexity.

There are 3 ways to implement preorder traversal: iterative, recursive and Morris.

Iterative and recursive approaches here do the job in one pass, but they both need up to \mathcal{O}(H) space to keep the stack, where H is a tree height.

Morris approach is two-pass approach, but it's a constant-space one.

Approach 1: Iterative Preorder Traversal.

Intuition

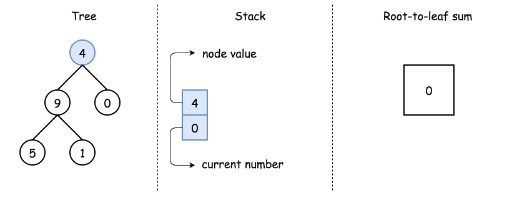
Here we implement standard iterative preorder traversal with the stack:

Push root into stack.
While stack is not empty:
- Pop out a node from stack and update the current number.
- If the node is a leaf, update root-to-leaf sum.
- Push right and left child nodes into stack.
Return root-to-leaf sum.

1 / 7

Implementation

Note, that Javadocs recommends to use ArrayDeque, and not Stack as a stack implementation.

Complexity Analysis

Time complexity: \mathcal{O}(N) since one has to visit each node.
Space complexity: up to \mathcal{O}(H) to keep the stack, where H is a tree height.

Approach 2: Recursive Preorder Traversal.

Iterative approach 1 could be converted into recursive one.

Recursive preorder traversal is extremely simple: follow Root->Left->Right direction, i.e. do all the business with the node (= update the current number and root-to-leaf sum), and then do the recursive calls for the left and right child nodes.

P.S. Here is the difference between preorder and the other DFS recursive traversals. On the following figure the nodes are numerated in the order you visit them, please follow 1-2-3-4-5 to compare different DFS strategies implemented as recursion.

Implementation

class Solution:
    def pseudoPalindromicPaths (self, root: TreeNode) -> int:
        count = 0
        
        stack = [(root, 0) ]
        while stack:
            node, path = stack.pop()
            if node is not None:
                # compute occurences of each digit 
                # in the corresponding register
                path = path ^ (1 << node.val)
                # if it's a leaf, check if the path is pseudo-palindromic
                if node.left is None and node.right is None:
                    # check if at most one digit has an odd frequency
                    if path & (path - 1) == 0:
                        count += 1
                else:
                    stack.append((node.right, path))
                    stack.append((node.left, path))
        
        return count

Complexity Analysis

Time complexity: \mathcal{O}(N) since one has to visit each node.
Space complexity: up to \mathcal{O}(H) to keep the recursion stack, where H is a tree height.

Approach 3: Morris Preorder Traversal.

We discussed already iterative and recursive preorder traversals, which both have great time complexity though use up to \mathcal{O}(H) to keep the stack. We could trade in performance to save space.

The idea of Morris preorder traversal is simple: to use no space but to traverse the tree.

How that could be even possible? At each node one has to decide where to go: to the left or tj the right, traverse the left subtree or traverse the right subtree. How one could know that the left subtree is already done if no additional memory is allowed?

The idea of Morris algorithm is to set the temporary link between the node and its predecessor: predecessor.right = root. So one starts from the node, computes its predecessor and verifies if the link is present.

There is no link? Set it and go to the left subtree.
There is a link? Break it and go to the right subtree.

There is one small issue to deal with : what if there is no left child, i.e. there is no left subtree? Then go straightforward to the right subtree.

Implementation

class Solution:
    def pseudoPalindromicPaths (self, root: TreeNode) -> int:
        def preorder(node, path):
            nonlocal count
            if node:
                path = path ^ (1 << node.val)
                if node.left is None and node.right is None:
                    if path & (path-1) == 0:
                        count += 1
                else:
                    preorder(node.left, path)
                    preorder(node.right, path)
        count = 0
        preorder(root, 0)
        return count

Complexity Analysis