110. Balanced Binary Tree
leetcode.com/problems/balanced-binary-tree/
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
Example 1:
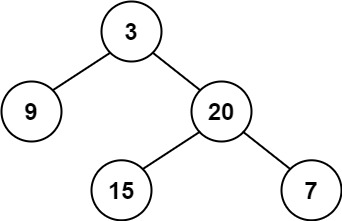
Input: root = [3,9,20,null,null,15,7] Output: true
Example 2:
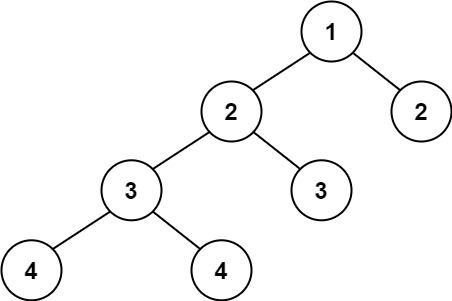
Input: root = [1,2,2,3,3,null,null,4,4] Output: false
Example 3:
Input: root = [] Output: true
Constraints:
- The number of nodes in the tree is in the range [0, 5000].
- -104 <= Node.val <= 104
Solution
Given the definition of a balanced tree we know that a tree T is not balanced if and only if there is some node p\in T such that |\texttt{height}(p.left) - \texttt{height}(p.right)| > 1. The tree below has each node is labeled by its height, as well as the unbalanced subtree highlighted.
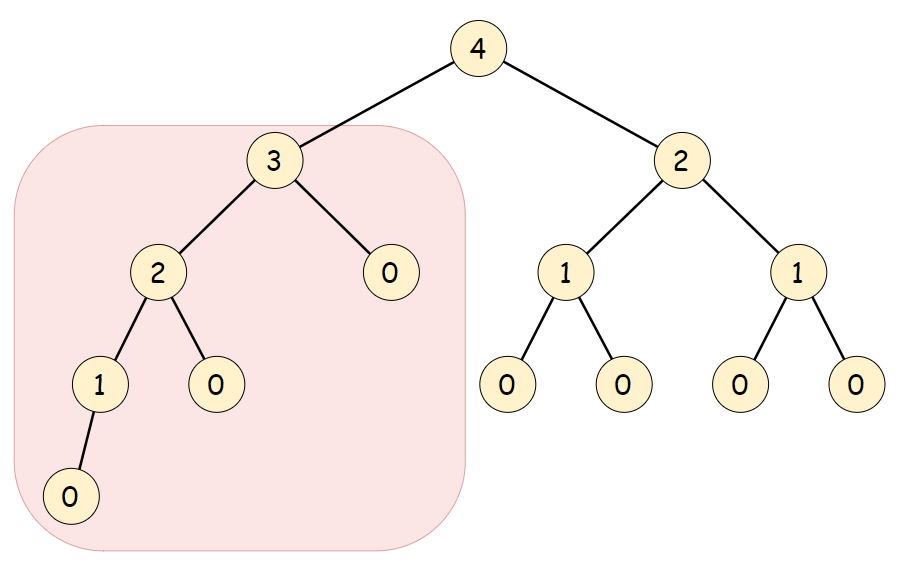
The balanced subtree definition hints at the fact that we should treat each subtree as a subproblem. The question is: in which order should we solve the subproblems?
Approach 1: Top-down recursion
Algorithm
First we define a function \texttt{height} such that for any node p\in T
\texttt{height}(p) = \begin{cases} -1 & p \text{ is an empty subtree i.e. } \texttt{null}\\ 1 + \max(\texttt{height}(p.left), \texttt{height}(p.right)) & \text{ otherwise} \end{cases}
Now that we have a method for determining the height of a tree, all that remains is to compare the height of every node's children. A tree T rooted at r is balanced if and only if the height of its two children are within 1 of each other and the subtrees at each child are also balanced. Therefore, we can compare the two child subtrees' heights then recurse on each one.
isBalanced(root): if (root == NULL): return true if (abs(height(root.left) - height(root.right)) > 1): return false else: return isBalanced(root.left) && isBalanced(root.right)
1 / 31
class Solution:
def height(self, root: TreeNode) -> int:
if not root:
return -1
return 1 + max(self.height(root.left), self.height(root.right))
def isBalanced(self, root: TreeNode) -> bool:
if not root:
return True
return abs(self.height(root.left) - self.height(root.right)) < 2 \
and self.isBalanced(root.left) \
and self.isBalanced(root.right)
Complexity Analysis
-
Time complexity : \mathcal{O}(n\log n)
-
For a node p at depth d, \texttt{height}(p) will be called d times.
-
We first need to obtain a bound on the height of a balanced tree. Let f(h) represent the minimum number of nodes in a balanced tree with height h. We have the relation
which looks nearly identical to the Fibonacci recurrence relation. In fact, the complexity analysis for f(h) is similar and we claim that the lower bound is f(h) = \Omega\left(\left(\frac{3}{2}\right)^h\right).
\begin{aligned} f(h+1) &= f(h) + f(h-1) + 1 \\ &> f(h) + f(h-1) & \qquad\qquad \text{This is the fibonacci sequence}\\ &\geq \left(\frac{3}{2}\right)^{h} + \left(\frac{3}{2}\right)^{h-1} & \text{via our claim} \\ &= \frac{5}{2} \left(\frac{3}{2}\right)^{h-1}\\ &> \frac{9}{4} \left(\frac{3}{2}\right)^{h-1} & \frac{9}{4} < \frac{5}{2}\\ &> \left(\frac{3}{2}\right)^{h+1} \end{aligned}Therefore, the height h of a balanced tree is bounded by \mathcal{O}(\log_{1.5}(n)). With this bound we can guarantee that \texttt{height} will be called on each node \mathcal{O}(\log n) times.
- If our algorithm didn't have any early-stopping, we may end up having \mathcal{O}(n^2) complexity if our tree is skewed since height is bounded by \mathcal{O}(n). However, it is important to note that we stop recursion as soon as the height of a node's children are not within 1. In fact, in the skewed-tree case our algorithm is bounded by \mathcal{O}(n), as it only checks the height of the first two subtrees.
-
-
Space complexity : \mathcal{O}(n). The recursion stack may contain all nodes if the tree is skewed.
Fun fact: f(n) = f(n-1) + f(n-2) + 1 is known as a Fibonacci meanders sequence.
Approach 2: Bottom-up recursion
Intuition
In approach 1, we perform redundant calculations when computing \texttt{height}. In each call to \texttt{height}, we require that the subtree's heights also be computed. Therefore, when working top down we will compute the height of a subtree once for every parent. We can remove the redundancy by first recursing on the children of the current node and then using their computed height to determine whether the current node is balanced.
Algorithm
We will use the same \texttt{height} defined in the first approach. The bottom-up approach is a reverse of the logic of the top-down approach since we first check if the child subtrees are balanced before comparing their heights. The algorithm is as follows:
Check if the child subtrees are balanced. If they are, use their heights to determine if the current subtree is balanced as well as to calculate the current subtree's height.
1 / 32
class Solution:
def isBalancedHelper(self, root: TreeNode) -> (bool, int):
if not root:
return True, 1
leftIsBalanced, leftHeight = self.isBalancedHelper(root.left)
if not leftIsBalanced:
return False, 0
rightIsBalanced, rightHeight = self.isBalancedHelper(root.right)
if not rightIsBalanced:
return False, 0
return (abs(leftHeight - rightHeight) < 2), 1 + max(leftHeight, rightHeight)
def isBalanced(self, root: TreeNode) -> bool:
return self.isBalancedHelper(root)[0]내코드, 위의 솔루션에서는 리턴을 두개 하니까 더 간결하다.
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
def dfs(node: TreeNode, depth: int) -> int:
if not node:
return depth
left_depth = dfs(node.left, depth+1)
right_depth = dfs(node.right, depth+1)
if left_depth == -1 or right_depth == -1:
return -1
if abs(left_depth - right_depth) <= 1:
return max(left_depth, right_depth)
else:
return -1
return True if dfs(root, 0) is not -1 else False
Complexity Analysis
-
Time complexity : \mathcal{O}(n)
For every subtree, we compute its height in constant time as well as compare the height of its children.
-
Space complexity : \mathcal{O}(n). The recursion stack may go up to \mathcal{O}(n) if the tree is unbalanced.
