163. Missing Ranges

leetcode.com/problems/missing-ranges/

 

You are given an inclusive range [lower, upper] and a sorted unique integer array nums, where all elements are in the inclusive range.

A number x is considered missing if x is in the range [lower, upper] and x is not in nums.

Return the smallest sorted list of ranges that cover every missing number exactly. That is, no element of nums is in any of the ranges, and each missing number is in one of the ranges.

Each range [a,b] in the list should be output as:

• "a->b" if a != b
• "a" if a == b

 

Example 1:

Input: nums = [0,1,3,50,75], lower = 0, upper = 99 Output: ["2","4->49","51->74","76->99"] Explanation: The ranges are: [2,2] --> "2" [4,49] --> "4->49" [51,74] --> "51->74" [76,99] --> "76->99"

Example 2:

Input: nums = [], lower = 1, upper = 1 Output: ["1"] Explanation: The only missing range is [1,1], which becomes "1".

Example 3:

Input: nums = [], lower = -3, upper = -1 Output: ["-3->-1"] Explanation: The only missing range is [-3,-1], which becomes "-3->-1".

Example 4:

Input: nums = [-1], lower = -1, upper = -1 Output: [] Explanation: There are no missing ranges since there are no missing numbers.

Example 5:

Input: nums = [-1], lower = -2, upper = -1 Output: ["-2"]

 

Constraints:

• -109 <= lower <= upper <= 109
• 0 <= nums.length <= 100
• lower <= nums[i] <= upper
• All the values of nums are unique.

 

 

---

Video Solution

---

 

 

Solution Article

---

Approach 1: Linear Scan

Intuition and Algorithm

Since the input array, nums, is sorted ascendingly and all the elements in it are within the given [lower, upper] bounds, we can simply check consecutive elements to see if they differ by one or not. If they don't, then we have found a missing range.

• When nums[i] - nums[i-1] == 1, we know that there are no missing elements between nums[i-1] and nums[i].
• When nums[i] - nums[i-1] > 1, we know that [nums[i-1] + 1, nums[i] - 1] range of elements are missing.

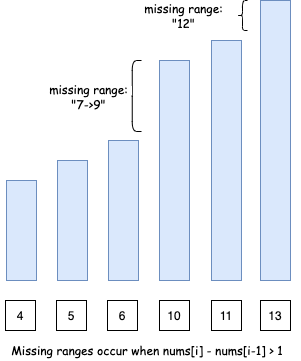
However, there are two edge cases:

• Case 1: If we don't start with lower as the first element of the array, we will need to consider [lower, num[0] - 1] missing range as well.

• Case 2: Similarly, if we don't end with upper as the last element of the array, we will need to consider [nums[n-1] + 1, upper] missing range as well. Note n here is the length of the input array nums.

 

 

class Solution {
    public List<String> findMissingRanges(int[] nums, int lower, int upper) {
        int n = nums.length;

        if (n == 0) {
            return Collections.singletonList(formatRange(lower, upper));
        }

        List<String> missingRanges = new ArrayList<>();

        // Edge case 1) Missing ranges at the beginning
        if (nums[0] > lower) {
            missingRanges.add(formatRange(lower, nums[0] - 1));
        }

        // Missing ranges between array elements
        for (int i = 1; i < n; ++i) {
            if (nums[i] - nums[i - 1] > 1) {
                missingRanges.add(formatRange(nums[i - 1] + 1, nums[i] - 1));
            }
        }
        
        // Edge case 2) Missing ranges at the end
        if (nums[n - 1] < upper) {
            missingRanges.add(formatRange(nums[n - 1] + 1, upper));
        }

        return missingRanges;
    }

    // formats range in the requested format
    String formatRange(int lower, int upper) {
        if (lower == upper) {
            return String.valueOf(lower);
        } else {
            return lower + "->" + upper;
        }
    }
}

 

Complexity Analysis

• Time complexity : O(N)O(N), where NN is the length of the input array. This is because we are only iterating over the array once.

• Space complexity : O(N)O(N) if we take the output into account and O(1)O(1) otherwise, where NN is the length of the input array. This is because we could have a missing range between each of the consecutive element of the input array. Hence, our output list that we need to return will be of size NN.