59. Spiral Matrix II

leetcode.com/problems/spiral-matrix-ii/

Spiral Matrix II - LeetCode

 

 

 

Overview

There are various problems in spiral matrix series with some variations like Spiral Matrix and Spiral Matrix III.

In order to solve such questions, the core idea is to decode the underlying pattern. This can be done by simulating the pattern and finding a generic representation that would work for any given nn. Let's discuss a few approaches.

---

Approach 1: Traverse Layer by Layer in Spiral Form

Intuition

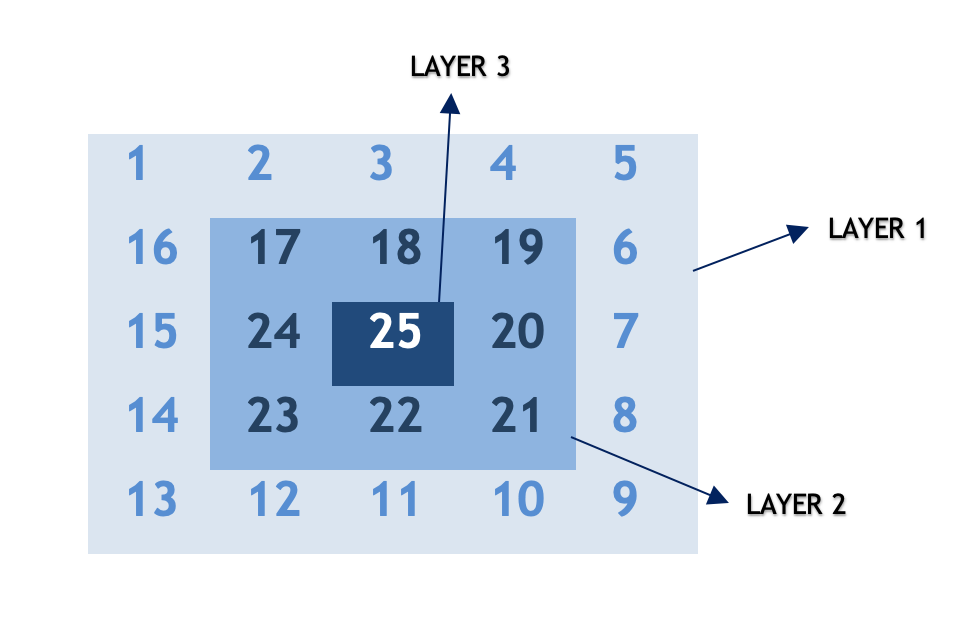
If we try to build a pattern for a given nn, we observe that the pattern repeats after completing one circular traversal around the matrix. Let's call this one circular traversal as layer. We start traversing from the outer layer and move towards inner layers on every iteration.

Algorithm

Let's devise an algorithm for the spiral traversal:

• We can observe that, for any given nn, the total number of layers is given by : \lfloor \frac{n+1}{2} \rfloor⌊2n+1​⌋ This works for both even and odd nn.

Example

For n = 3n=3, layers = 2layers=2

For n = 6n=6, total layers = 3layers=3

• Also, for each layer, we traverse in at most 4 directions :

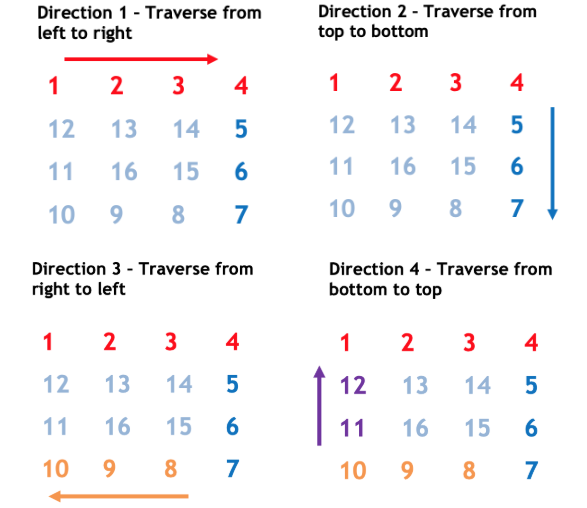
In every direction, either row or column remains constant and other parameter changes (increments/decrements).

Direction 1: From top left corner to top right corner.

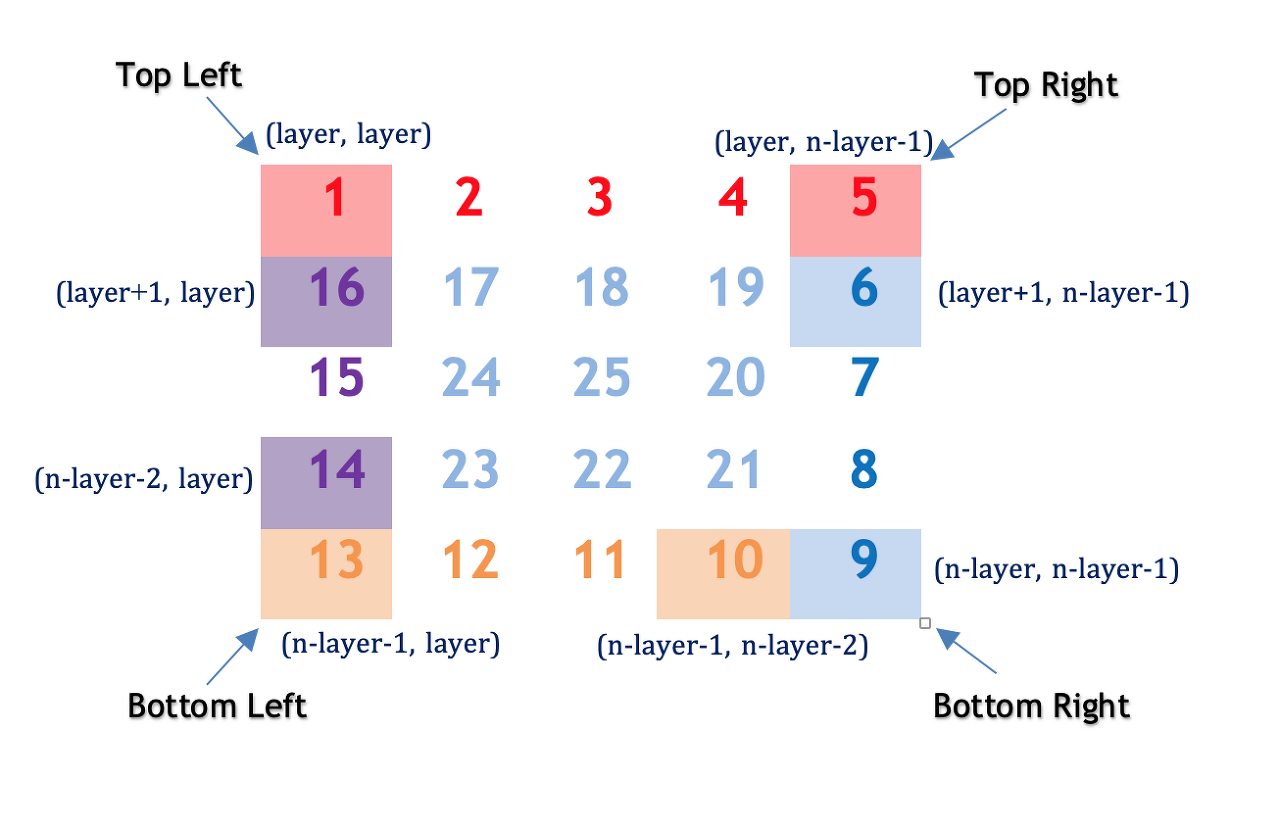
The row remains constant as \text{layer}layer and column increments from \text{layer}layer to n-\text{layer}-1n−layer−1

Direction 2: From top right corner to the bottom right corner.

The column remains constant as n-layer-1n−layer−1 and row increments from \text{layer}+1layer+1 to n-\text{layer}n−layer.

Direction 3: From bottom right corner to bottom left corner.

The row remains constant as n-\text{layer}-1n−layer−1 and column decrements from n-\text{layer}-2n−layer−2 to \text{layer}layer.

Direction 4: From bottom right corner to top left corner.

The column remains constant as \text{layer}layer and column decrements from n-\text{layer}-2n−layer−2 to \text{layer}+1layer+1.

This process repeats (n+1)/2(n+1)/2 times until all layers are traversed.

 

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] result = new int[n][n];
        int cnt = 1;
        for (int layer = 0; layer < (n + 1) / 2; layer++) {
            // direction 1 - traverse from left to right
            for (int ptr = layer; ptr < n - layer; ptr++) {
                result[layer][ptr] = cnt++;
            }
            // direction 2 - traverse from top to bottom
            for (int ptr = layer + 1; ptr < n - layer; ptr++) {
                result[ptr][n - layer - 1] = cnt++;
            }
            // direction 3 - traverse from right to left
            for (int ptr = layer + 1; ptr < n - layer; ptr++) {
                result[n - layer - 1][n - ptr - 1] = cnt++;
            }
            // direction 4 - traverse from bottom to top
            for (int ptr = layer + 1; ptr < n - layer - 1; ptr++) {
                result[n - ptr - 1][layer] = cnt++;
            }
        }
        return result;
    }
}

 

Complexity Analysis

• Time Complexity: \mathcal{O}(n^2)O(n2). Here, nn is given input and we are iterating over n\cdot nn⋅n matrix in spiral form.
• Space Complexity: \mathcal{O}(1)O(1) We use constant extra space for storing cntcnt.

---

Approach 2: Optimized spiral traversal

Intuition

Our main aim is to walk in a spiral form and fill the array in a particular pattern. In the previous approach, we used a separate loop for each direction. Here, we discuss another optimized to achieve the same result.

Algorithm

• We have to walk in 4 directions forming a layer. We use an array dirdir that stores the changes in xx and yy co-ordinates in each direction.

Example

In left to right walk ( direction #1 ), xx co-ordinates remains same and yy increments (x = 0x=0, y = 1y=1).

In right to left walk ( direction #3 ), xx remains same and yy decrements (x = 0x=0, y = -1y=−1).

Using this intuition, we pre-define an array dirdir having xx and yy co-ordinate changes for each direction. There are a total of 4 directions as discussed in the previous approach.

• The \text{row}row and colcol variables represent the current xx and yy co-ordinates respectively. It updates based on the direction in which we are moving.

How do we know when we have to change the direction?

When we find the next row or column in a particular direction has a non-zero value, we are sure it is already traversed and we change the direction.

Let dd be the current direction index. We go to next direction in array dirdir using (d+ 1) \% 4(d+1)%4. Using this we could go back to direction 1 after completing one circular traversal from direction 1 to direction 4 .

It must be noted that we use floorMod in Java instead of modulo \%% to handle mod of negative numbers. This is required because row and column values might go negative and using \%% won't give desired results in such cases.

 

이 방법으로 풀었으나 내 코드와는 큰 차이가 있다. 여기서는 floorMod를 사용해 해당 셀이 이미 채워져 있다면 방향을 바꾸도록 했다.

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] result = new int[n][n];
        int cnt = 1;
        int dir[][] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        int d = 0;
        int row = 0;
        int col = 0;
        while (cnt <= n * n) {
            result[row][col] = cnt++;
            int r = Math.floorMod(row + dir[d][0], n);
            int c = Math.floorMod(col + dir[d][1], n);

            // change direction if next cell is non zero
            if (result[r][c] != 0) d = (d + 1) % 4;

            row += dir[d][0];
            col += dir[d][1];
        }
        return result;
    }
}

 

Complexity Analysis

• Time Complexity: \mathcal{O}(n^2)O(n2). Here, nn is given input and we are iterating over n\cdot nn⋅n matrix in spiral form.
• Space Complexity: \mathcal{O}(1)O(1) We use constant extra space for storing cntcnt.