1658. Minimum Operations to Reduce X to Zero
1658. Minimum Operations to Reduce X to Zero
Medium
4569Add to ListShare
You are given an integer array nums and an integer x. In one operation, you can either remove the leftmost or the rightmost element from the array nums and subtract its value from x. Note that this modifies the array for future operations.
Return the minimum number of operations to reduce x to exactly 0 if it's possible, otherwise, return -1.
Example 1:
Input: nums = [1,1,4,2,3], x = 5 Output: 2 Explanation: The optimal solution is to remove the last two elements to reduce x to zero.
Example 2:
Input: nums = [5,6,7,8,9], x = 4 Output: -1
Example 3:
Input: nums = [3,2,20,1,1,3], x = 10 Output: 5 Explanation: The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
Constraints:
- 1 <= nums.length <= 105
- 1 <= nums[i] <= 104
- 1 <= x <= 109
Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray.
Finding the maximum subarray is standard and can be done greedily.
Solution
Overview
This problem is closely related to Maximum Size Subarray Sum Equals k. The key difference is that the input array for this problem only contains positive integers, whereas for Maximum Size Subarray Sum Equals k, it can contain both positive and negative integers.
One way of solving this problem is to firstly transform it into a Maximum Size Subarray Sum Equals k problem. Then, any algorithm that solves Maximum Size Subarray Sum Equals k will also solve this problem.
Warning: The converse is not true. Because the input array for Maximum Size Subarray Sum Equals k can contain both positive and negative integers, algorithms that only work for positive integers will work for this problem, but not Maximum Size Subarray Sum Equals k.
The downside of doing this is that the algorithms for Maximum Size Subarray Sum Equals k are more complicated than what is necessary for this problem, so in this article, we're going to focus on approaches that only work with positive integers.
Below, we will discuss two methods: Two Pointers (Indirectly) and Two Pointers (Directly). Their implementations are almost the same, but their perspectives on the problem are different.
Approach 1: Two Pointers (Indirectly)
Intuition
The indirect approach determines which values will remain in the array, as opposed to which values should be removed from the array.
Let total be the sum of elements in nums.
An insight is that:
To find the shortest required operations that sum up to x is to find the longest subarray that sums up to total - x.
For example:
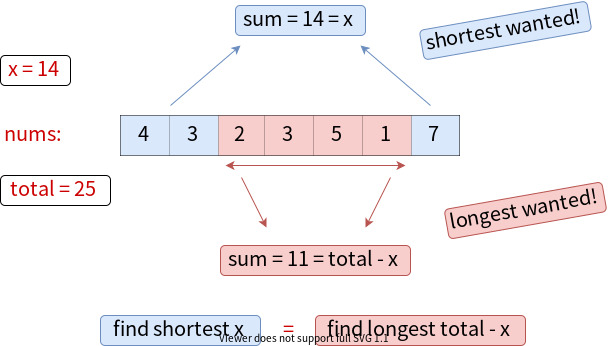
In this case, nums = [4, 3, 2, 3, 5, 1, 7]. To sum to x = 14, the shortest operations are taking [4, 3] on left and [7] on right. This is the same as finding the longest subarray that sums up to total - x = 11: what we need is the remaining subarray: [2, 3, 5, 1].
In this way, we've changed the problem into finding the maximum sized subarray with sum equals total - x".
What we can do is to use two pointers to solve it.
We initialize two pointers left and right. Iterate right pointer from the start to the end of nums. In each position of right pointer, we move left pointer as left as possible until the subarray sum is equal to or less than the required total - x.
With this moving method, we can find the subarray [left, ..., right] whose sum is closest to total - x for each right (but not greater than).
Take nums = [1, 3, 2, 3, 5, 1, 7] and x = 14 for example.
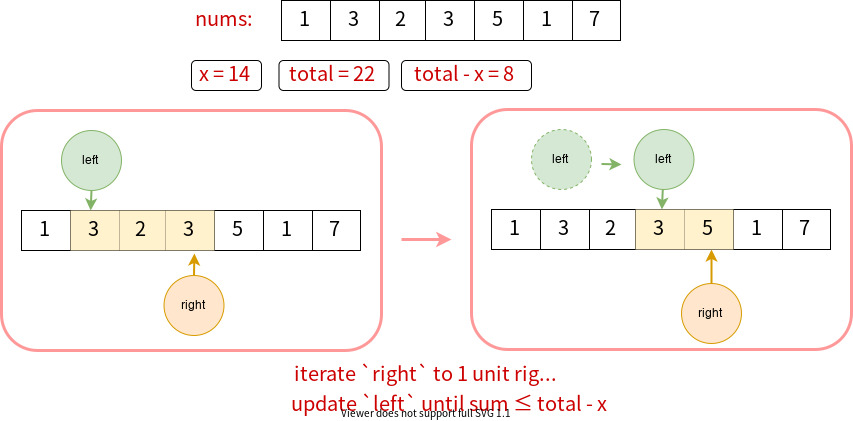
When left = 1 and right =3, currently the subarray sum is 3 + 2 + 3 = 8. The current sum is closest to total - x = 8 (In fact, they are the same!).
If we want to move right to one unit right, the sum becomes 3 + 2 + 3 + 5 = 13 > 8. Then we need to move left to let sum as close to total - x as possible.
Moving left one unit right yields 2 + 3 + 5 = 10 > 8. One more unit right gives 3 + 5 = 8 = total - x. Here we stop moving left since it is equal to the required total - x. In this case, we found the subarray whose sum is closest to 8 and ends at right.
With those two pointers, we can find all subarray whose sum is total - x. What we need to do is to record the maximum length of those subarrays.
Finally, calculate the remaining number of elements in nums and that is the final answer.
Algorithm
Step 1: Calculate the total sum of nums. Mark as total.
Step 2: Initialize two pointers left and right to 0. Initialize an integer current to represent the sum from nums[left] to nums[right], inclusively. Initialize an integer maxi to record the maximum length that sums up to total - x.
Step 3: Iterate right form 0 to the end of nums. In each iteration:
- Update current.
- If current is greater than total - x, move left to left.
- If current is equal to total - x, update the maximum length.
Step 4: Return the result.
Implementation
class Solution:
def minOperations(self, nums: List[int], x: int) -> int:
total = sum(nums)
n = len(nums)
maxi = -1
left = 0
current = 0
for right in range(n):
# sum([left ,..., right]) = total - x
current += nums[right]
# if larger, move `left` to left
while current > total-x and left <= right:
current -= nums[left]
left += 1
# check if equal
if current == total-x:
maxi = max(maxi, right-left+1)
return n-maxi if maxi != -1 else -1
Complexity Analysis
Let NN be the length of nums.
-
Time Complexity: \mathcal{O}(N)O(N), since each element is accessed at most twice, once by left and once by right.
-
Space Complexity: \mathcal{O}(1)O(1), since no additional data structure is allocated.
Approach 2: Two Pointers (Directly)
Intuition
In the previous approach, we transformed the problem into finding the longest subarray with a sum of total - x. A natural question that begs to be asked is, "Can we solve it directly without transformation?".
Yes, we can. Let's have a try.
Similarly, we would like to continue using two pointers.
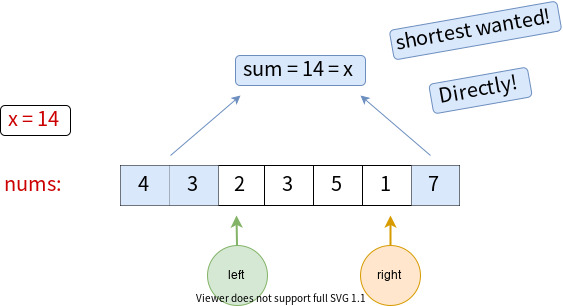
This time, we mark sum as the sum of the left part from left and the right part from right, not including left and right. Of course, you can include them with a few modifications to the code.
Still, we need to iterate right from the start to the end of nums and move left correspondingly. Here, we choose to move left to left until sum is greater than or equals to x.
We still take nums = [1, 3, 2, 3, 5, 1, 7] and x = 14 for example.
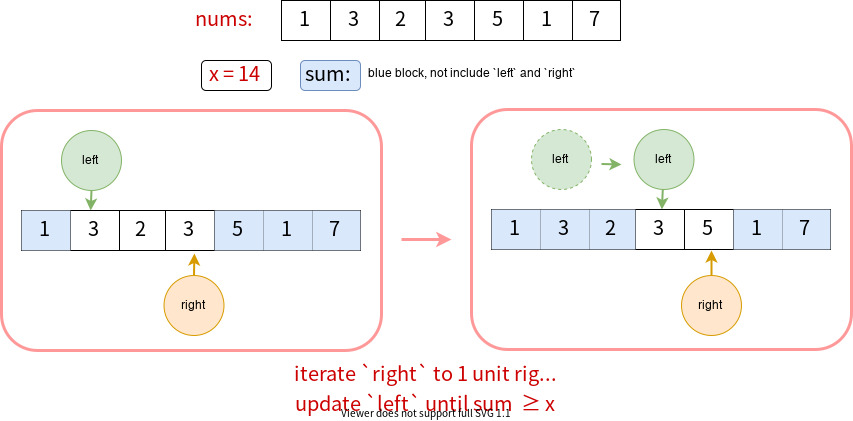
When left = 1 and right = 3, currently the sum is 1 + 5 + 1 + 7 = 14, which is closest to x = 14 (In fact, they are the same!). If we want to move right pointer by one unit towards right, the sum becomes 1 + 1 + 7 = 9 < 14. Then we need to move left to let sum as close to x as possible.
Moving left pointer one unit towards right yields 1 + 3 + 1 + 7 = 12 < 14. One more unit towards right gives 1 + 3 + 2+ 1 + 7 = 14 = x. Here we stop moving left pointer since it is equal to x.
With those two pointers, we can find all operations whose sum is x. What we need to do is to record the minimal length and return it.
However, it is needed to point out that the difference between Approach 1 and Approach 2 is not that huge. Their codes are similar but differ in the perspectives of the problem.
Algorithm
Step 1: Calculate the total sum of nums.
Step 2: Initialize two pointers left and right to 0. Initialize an integer current to represent the sum from nums[0] to nums[left-1] and from nums[right+1] to nums[last]. Initialize an integer mini to record the minimum length that sums up to x
Step 3: Iterate right form 0 to the end of nums. In each iteration:
- Update current.
- If current is smaller than x, move left to left.
- If current is equal to x, update the maximum length.
Step 4: Return the result.
Implementation
class Solution:
def minOperations(self, nums: List[int], x: int) -> int:
current = sum(nums)
n = len(nums)
mini = inf
left = 0
for right in range(n):
# sum([0,..,left) + (right,...,n-1]) = x
current -= nums[right]
# if smaller, move `left` to left
while current < x and left <= right:
current += nums[left]
left += 1
# check if equal
if current == x:
mini = min(mini, (n-1-right)+left)
return mini if mini != inf else -1
Complexity Analysis
Let NN be the length of nums.
-
Time Complexity: \mathcal{O}(N)O(N), since each element is accessed at most twice, once by left pointer and once by right pointer.
-
Space Complexity: \mathcal{O}(1)O(1), since no additional data structure is allocated.





