Jump game series 점프게임 시리즈
점프게임 시리즈 공부하기
leetcode.com/problemset/all/?search=jump%20game
6개나 있네. 2,4 가 구글 기출문제이다.
55. Jump Game
leetcode.com/problems/jump-game/
미디움
그냥 도달하기만 하면 되는거라서, 그리디로 짜면 된다.
내 코드
class Solution:
def canJump(self, nums: List[int]) -> bool:
reachable = 0
for i in range(len(nums)):
if i <= reachable:
reachable = max(reachable, i + nums[i])
if reachable >= len(nums)-1:
return True
return True if reachable >= len(nums)-1 else False일주일전에는 이렇게 짰다는게 웃기다 ㅋㅋ
class Solution:
def canJump(self, nums: List[int]) -> bool:
n = len(nums)
i = 0
next_dest = 1 + i + nums[i]
while i < next_dest and i < n:
next_dest = max(next_dest, 1 + i + nums[i])
i += 1
return True if next_dest >= n else False솔루션 코드
public class Solution {
public boolean canJump(int[] nums) {
int lastPos = nums.length - 1;
for (int i = nums.length - 1; i >= 0; i--) {
if (i + nums[i] >= lastPos) {
lastPos = i;
}
}
return lastPos == 0;
}
}
결과
class Solution:
def canJump(self, nums: List[int]) -> bool:
furthest = 0
last_index = len(nums)-1
i=0
while(i<=furthest and furthest<last_index):
furthest = max(furthest,nums[i]+i)
i+=1
return furthest>=last_index
class Solution:
def canJump(self, nums: List[int]) -> bool:
reachable=0
for i in range(len(nums)):
if reachable<i:
return False
reachable=max(reachable,i+nums[i])
return True
class Solution:
def canJump(self, nums: List[int]) -> bool:
made_it = False
target = 0
for i in range(1,len(nums)):
idx = len(nums) - 1 - i
if nums[idx] >= i - target:
target = i
return target == len(nums)-1
새해맞아 다시 짜본 코드는..
class Solution:
def canJump(self, nums: List[int]) -> bool:
reachable = 0
i = 0
while i <= reachable:
reachable = max(reachable, i + nums[i])
if reachable >= len(nums)-1:
return True
i += 1
return False
45. Jump Game II
leetcode.com/problems/jump-game-ii/
HARD, 구글기출
앞 문제의 reachable을 이용하되 이번에는 min_steps을 구해준다.
실제 jumps를 구현하여, max_jump으로 가지 못할경우에만 jump를 한번 더 하는것으로 계산.
max_steps는 한걸음씩 가는것으로 구현하면 되고 따라서 max_steps이 갱신될 때의 reachable이다.
class Solution:
def jump(self, nums: List[int]) -> int:
n = len(nums)
if n < 2:
return 0
max_steps = nums[0]
reachable = nums[0]
jumps = 1
for i in range(1, n):
if max_steps < i:
jumps += 1
max_steps = reachable
reachable = max(reachable, nums[i] + i)
return jumps
변수 이름은 나만 헷갈리나?
class Solution:
def jump(self, nums: List[int]) -> int:
n = len(nums)
if n < 2:
return 0
reachable = nums[0]
next_reachable = nums[0]
jumps = 1
for i in range(1, n):
if reachable < i:
jumps += 1
reachable = next_reachable
next_reachable = max(next_reachable, nums[i] + i)
return jumps
1306. Jump Game III
leetcode.com/problems/jump-game-iii/
+k,-k의 점프를 통해서 n-1에 도달 할 수 있다/없다 를 구하는 문제
그냥 BFS와 DFS로 풀면 되는 문제
BFS
class Solution:
def canReach(self, arr: List[int], start: int) -> bool:
n = len(arr)
q = [start]
while q:
node = q.pop(0)
if arr[node] == 0:
return True
if arr[node] < 0:
continue
for i in [node+arr[node], node-arr[node]]:
if 0 <= i < n:
q.append(i)
arr[node] = -arr[node]
return False
DFS
class Solution:
def canReach(self, arr: List[int], start: int) -> bool:
if 0 <= start < len(arr) and arr[start] >= 0:
if arr[start] == 0:
return True
arr[start] = -arr[start]
return self.canReach(arr, start+arr[start]) or self.canReach(arr, start-arr[start])
return False
내코드
솔루션 보면 중간에 for 문이 예쁨
class Solution:
def canReach(self, arr: List[int], start: int) -> bool:
n = len(arr)
q = [start]
while q:
cur = q.pop(0)
if arr[cur] == 0:
return True
if arr[cur] < 0:
continue
if cur + arr[cur] < n:
q.append(cur + arr[cur])
if 0 <= cur - arr[cur]:
q.append(cur - arr[cur])
arr[cur] = -arr[cur]
return False
1345. Jump Game IV
leetcode.com/problems/jump-game-iv/
HARD / 구글,아마존
1340. Jump Game V
leetcode.com/problems/jump-game-v/
HARD / 잘안나옴
1696. Jump Game VI
leetcode.com/problems/jump-game-vi/
미디움 / 잘안나옴
현재+1 ~ 현재+k 까지 점프하여 n-1 에 도달했을때, 최대 배열값의 합을 구하는 문제이다. [i + 1, min(n - 1, i + k)]
슬라이딩윈도우 + max_heap 조합, 왜 태그에 dequeue 덱이라고 되있는지 한번 살펴보자.
Solution
Overview
You probably can guess from the problem title, this is the sixth problem in the series of Jump Game problems. Those problems are similar, but have considerable differences, making their solutions quite different.
In this problem, for each move, we are allowed to advance k steps, and our target is to maximize the scores we collect.
One example:
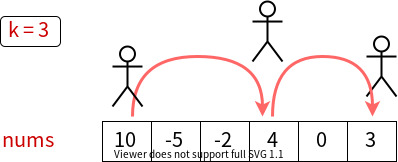
Below, five approaches are introduced.
Generally, we recommend Approach 1: Dynamic Programming + Deque and Approach 4: Dynamic Programming + Deque (Compressed) since they have the best performance.
Also, because it is a medium level problem, we allow some relevant slower approaches: Approach 2: Dynamic Programming + Priority Queue and Approach 3: Segment Tree.
Note that Approach 4: Dynamic Programming + Deque (Compressed) and Approach 5: Dynamic Programming + Priority Queue (Compressed) are the state compressed version of Approach 1 and Approach 2.
Approach 1: Dynamic Programming + Deque
Intuition
Note: This approach is a little bit beyond the medium level question, so if you are struggling to understand this, you should at least finish the DP part, and then feel free to jump to Approach 2 , which is easier but has a slower performance.
However, it is still strongly recommended to understand this whole approach since it is not that hard.
In this part, we will explain how to think of this approach step by step.
If you are only interested in the pure algorithm, you can jump to the algorithm part.
For the Jump Game series questions, dynamic programming is our old friend. It's natural to try DP first.
To implement DP, we need a dp array. What should the DP array represent?
Since the problem ask us the max score we can get ending at the last index, how about letting dp[i] represent the max score we can get ending at index i?
Also, you can let dp[i] represent the max score we can get starting at index i. That is similar.
To have better naming, we rename dp to score. So, score[i] represents the max score we can get ending at index i.
For example:
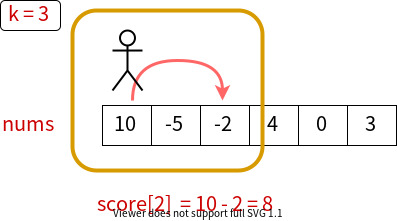
OK. Let's dive deeper.
For a DP solution, basically, we need two things:
- The base case.
This is where our dp start. Usually, this means how to calculate dp[0]. In our case, score[0] = nums[0] since nums[0] is both our start and end. We only have one choice.
- The so-called transition equation.
That is to say, if we have already calculated score[0], score[1], ..., score[i-1], how can we calculate score[i]?
Since we can only advance k steps, to arrive nums[i], we must jump from one of nums[i-k], nums[i-k+1], ..., nums[i-1]. We only need to pick the one with maximum score.
For example, if we are calculating score[3] and k=3, we need to decide jump from index 0, 1, or 2:
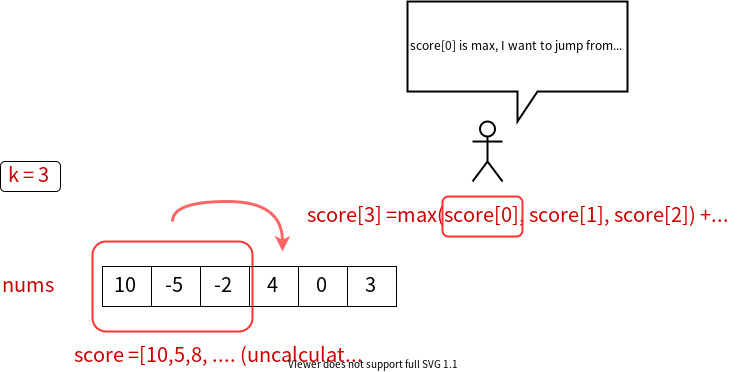
OK, now we have a transition equation:
score[i] = max(score[i-k], ..., score[i-1]) + nums[i]
However, this equation needs \mathcal{O}(k)O(k) to calculate score[i], which makes the overall complexity come to \mathcal{O}(Nk) = 10^{9}O(Nk)=109 in the worst case, given that NN is the length of nums.
This complexity is too much and we need to improve it.
Somehow, this equation is similar to Sliding Window Maximum, which is a typical monotonic queue problem. We can use the same technique to make some improvements.
Note that when calculating maximum, we do not need all score[i-k], ..., score[i-1]; we just need some large values.
For example, if k == 3 and [score[i-3], score[i-2], score[i-1]] = [2, 4, 10], their maximum is score[i-1] = 10. In this case, when calculating following score[i] (and further score[i+1]), we do not need score[i-3] = 2 and score[i-2] = 4, since they are smaller than score[i-1] = 10.
The picture illustrates another example when calculating score[2]:
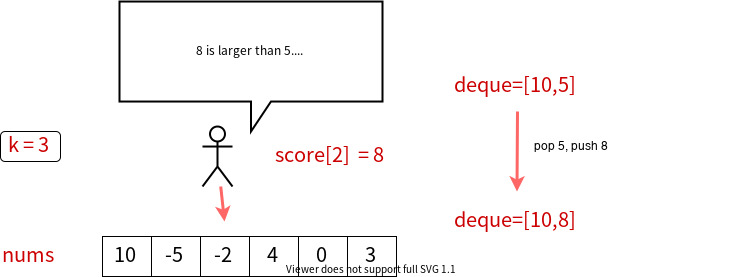
In this case, we maintain a deque as a monotonically decreasing queue. Since it is monotonically decreasing, the maximum value is always at the top of the queue.
In practice, since we store scores in score, we only need to store the index in the queue.
Also, remember to pop the index smaller than i-k out of the queue from the left.
Algorithm
Step 1: Initialize a dp array score, where score[i] represents the max score starting at nums[0] and ending at nums[i].
Step 2: Initialize a deque array dq storing indexes of nums such that the corresponding values are monotonically decreasing.
Step 3: Iterate over nums. For each element nums[i]:
- Pop all the indexes smaller than i-k out of dq from left.
- Update score[i] to score[dq.peekFirst()] + nums[i].
- If the corresponding score of the rightmost index in dq (i.e., score[dq.peekLast()]) is smaller than score[i], pop it from the right to make corresponding values monotonically decreasing. Repeat.
- Push i into the right of dq.
Step 4: Return the last element of score.
Challenge: Can you implement the code yourself without seeing our implementations?
Implementation
Complexity Analysis
Let NN be the length of nums.
-
Time Complexity: \mathcal{O}(N)O(N), since we need to iterate nums, and push and pop each element into the deque at most once.
-
Space Complexity: \mathcal{O}(N)O(N), since we need \mathcal{O}(N)O(N) space to store our dp array and \mathcal{O}(k)O(k) to store dq.
Approach 2: Dynamic Programming + Priority Queue
Intuition
In Approach 1, we got the following transition equation for Dynamic Programming:
score[i] = max(score[i-k], ..., score[i-1]) + nums[i]
If you are not familiar with the monotonic queue technique mentioned in Approach 1, and still want to find out the maximum quickly, Priority Queue (Heap) is for you. Heap maintain and return the max value in \loglog time.
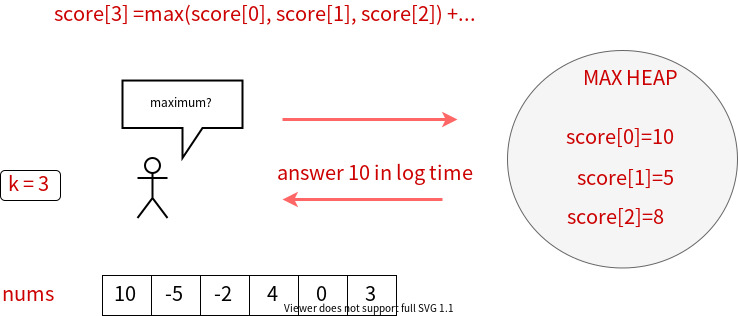
If we found that the index of the maximum score is less than i-k, just pop out and get the next maximum score.
Algorithm
Step 1: Initialize a dp array score, where score[i] represents the max score starting at nums[0] and ending at nums[i].
Step 2: Initialize a max-heap priority_queue.
Step 3: Iterate over nums. For each element nums[i]:
- If the index of top of priority_queue is less than i-k, pop the top. Repeat.
- Update score[i] to the sum of corresponding score of the index of top of priority_queue and nums[i] (i.e., score[priorityQueue.peek()[1]] + nums[i]).
- Push pair (score[i], i) into priority_queue.
Step 4: Return the last element of score.
Challenge: Can you implement the code yourself without seeing our implementations?
Implementation
Complexity Analysis
Let NN be the length of nums.
-
Time Complexity: \mathcal{O}(N \log N)O(NlogN), since we need to iterate nums, and push and pop each element into the deque at most once, and for each push and pop, it costs \mathcal{O}(\log N)O(logN) in the worst case.
-
Space Complexity: \mathcal{O}(N)O(N), since we need \mathcal{O}(N)O(N) space to store our dp array and \mathcal{O}(N)O(N) to store priority_queue.
Approach 3: Segment Tree
Intuition
In Approach 1, we got the following transition equation for Dynamic Programming:
score[i] = max(score[i-k], ..., score[i-1]) + nums[i]
There is also another way to find out the interval maximum in \loglog time: Segment Tree.
Since we already have some great explanations on Segment Tree, here we will not provide a detailed explanation of implementation. You can find some comprehensive tutorials on Recursive Approach to Segment Trees or Range Sum Query - Mutable.
Now, we will have a quick review of the segment tree and then explain how we can use it to tackle our problem.
As we know, the segment tree is a data structure used for storing information about intervals. Given that NN is the size of the tree, this data structure allows us to query and to update the information about a certain interval in \mathcal{O}(\log(N))O(log(N)) time.
Take the segment tree for querying interval max for an example:
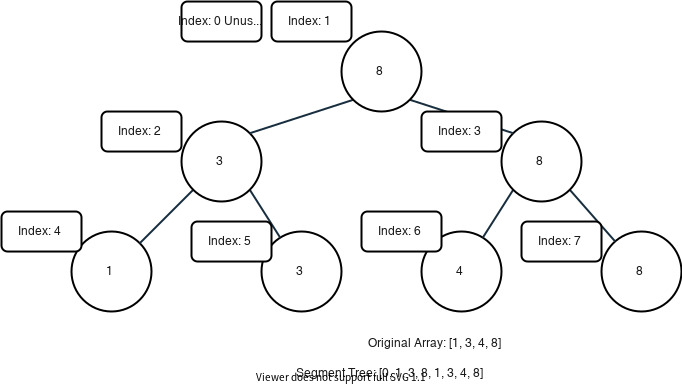
Usually, we store the tree in an array. We need twice the size of the original array to store the segment tree.
Here, we leave the index 0 unused for the convenience of indexing. You can also choose to use it by shifting the whole tree to left by one unit. In our approach, the left and right children of node i are 2*i and 2*i + 1 respectively.
Given that n is the size of the original array, from the node n to node 2*n - 1, we store the original array itself. For other nodes, we store the value of node i as the sum of node 2*i and node 2*i + 1.
The segment tree allows us to query the max of a certain interval and to update the values of elements. It should be able to process both actions in \mathcal{O}(\log(N))O(log(N)) time. Let's see some examples.
Updating Value
For update, what we do is simple. Just update the value from the leaf to the root. For instance:
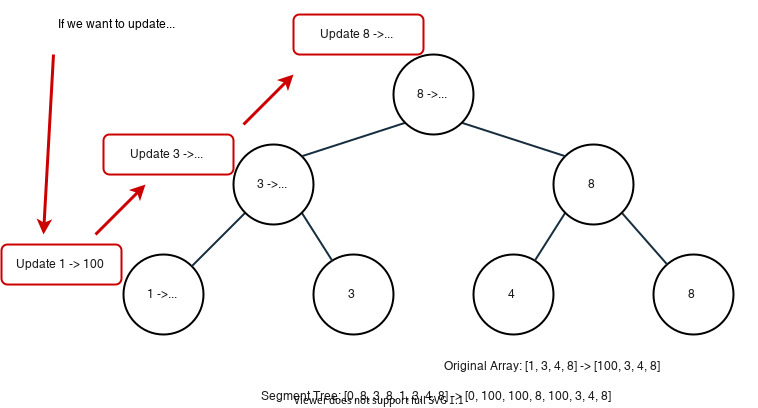
Querying Sum
For query, the case is a bit complicated. Generally speaking, we are dividing the target interval into a few pre-calculated segments to reduced run time. For example:
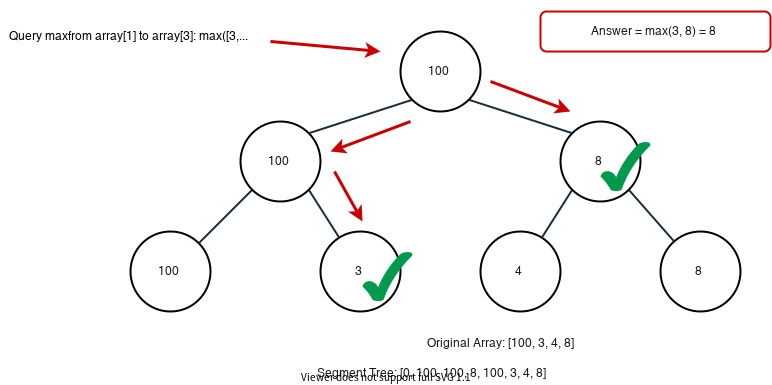
OK. Now back to our problem. How can we use the segment tree?
For each element nums[i], we need to query max(score[i-k], ..., score[i-1]), and then update the value of index i in Segment Tree to that maximum plus nums[i]. Both actions can be implemented in \loglog time.
Algorithm
Step 1: Implement the Segment Tree. Since the tree is initialized to all zeros, only update and query need to be implemented.
Step 2: Iterate over nums. For each element nums[i]:
- query the maximum from index i-k to index i.
- update value of index i to that maximum plus nums[i].
Step 3: Return the last element of the segment tree.
Challenge: Can you implement the code yourself without seeing our implementations?
Implementation
Complexity Analysis
Let NN be the length of nums.
-
Time Complexity: \mathcal{O}(N \log N)O(NlogN), since we need to iterate nums, and for each element we need to perform the query and update once, which costs \mathcal{O}(\log N)O(logN) in the worst case.
-
Space Complexity: \mathcal{O}(N)O(N), since we need \mathcal{O}(N)O(N) space to store our segment tree.
Approach 4: Dynamic Programming + Deque (Compressed)
Intuition
Note that in Approach 1, when calculating score[i], we do not need all values from score[0] to score[i-1]; we only need part of values from score[i-k] to score[i-1]. We can drop the previous values to save memory.
But how? Note that we have a deque array dq, we can save score[i] when saving index i, and drop the whole score array. That is to say, we save a pair (i, score[i]) in the deque. The length of dq is at most \mathcal{O}(k)O(k), so the space complexity is down to \mathcal{O}(k)O(k).
Algorithm
Step 1: Initialize an integer score.
Step 2: Initialize a deque array dq.
Step 3: Iterate over nums. For each element nums[i]:
- Pop all the indexes smaller than i-k out of dq from left.
- Update score to dq.peekFirst()[1] + nums[i].
- If the corresponding score of the rightmost index in dq (i.e., dq.peekLast()[1]) is smaller than score, pop it from the right to make corresponding values monotonically decreasing. Repeat.
- Push (i, score) into the right of dq.
Step 4: Return score.
Challenge: Can you implement the code yourself without seeing our implementations?
Implementation
Complexity Analysis
Let NN be the length of nums.
-
Time Complexity: \mathcal{O}(N)O(N), since we need to iterate nums, and push and pop each element into the deque at most once.
-
Space Complexity: \mathcal{O}(k)O(k), since we need \mathcal{O}(k)O(k) to store dq.
Approach 5: Dynamic Programming + Priority Queue (Compressed)
Intuition
Similar to Approach 4, when calculating score[i], we do not need all values from score[0] to score[i-1]; we only need values from score[i-k] to score[i-1]. We can drop the previous values to save memory.
Since we already save the (score[i], i) pair in our Priority Queue, we can directly drop the score array.
However, the length of our Priority Queue is \mathcal{O}(N)O(N) in the worst case, given that NN is the length of nums. That is to say, we can not decrease the big-O space complexity. Nevertheless, we still decrease memory usage by half by dropping the score array.
Algorithm
Step 1: Initialize an integer score.
Step 2: Initialize a max-heap priority_queue.
Step 3: Iterate over nums. For each element nums[i]:
- If the index of top of priority_queue is less than i-k, pop the top. Repeat.
- Update score to the sum of corresponding score of the index of top of priority_queue and nums[i] (i.e., priorityQueue.peek()[0] + nums[i]).
- Push pair (score, i) into priority_queue.
Step 4: Return score.
Challenge: Can you implement the code yourself without seeing our implementations?
Implementation
Complexity Analysis
Let NN be the length of nums.
-
Time Complexity: \mathcal{O}(N \log N)O(NlogN), since we need to iterate nums, and push and pop each element into the deque at most once, and for each push and pop, it costs \mathcal{O}(\log N)O(logN) in the worst case.
-
Space Complexity: \mathcal{O}(N)O(N), since we need \mathcal{O}(N)O(N) to store priority_queue.





