Math - Top Interview Questions[Medium] (8/9) : Python
Math
Most of the math questions asked in interviews do not require math knowledge beyond middle school level.
We recommend: Excel Sheet Column Number, Pow(x, n) and Divide Two Integers.
Happy Number
Factorial Trailing Zeroes
Excel Sheet Column Number
Pow(x, n)
Sqrt(x)
Divide Two Integers
Fraction to Recurring Decimal
202. Happy Number
leetcode.com/problems/happy-number/
4가지 방식이 있는데 하나는 logN / logN 나머지는 전부 logN/1 이다.
3,4번은 숫자를 미리 알고 하드코드 하는 방식이므로 안본다.
문제를 잘 읽어보면 알수있듯이, 사이클을 감지하는 알고리즘이 필요하다.
Write an algorithm to determine if a number n is happy.
A happy number is a number defined by the following process:
- Starting with any positive integer, replace the number by the sum of the squares of its digits.
- Repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1.
- Those numbers for which this process ends in 1 are happy.
Return true if n is a happy number, and false if not.
Example 1:
Input: n = 19 Output: true Explanation: 12 + 92 = 82 82 + 22 = 68 62 + 82 = 100 12 + 02 + 02 = 1
Example 2:
Input: n = 2 Output: false
Constraints:
- 1 <= n <= 231 - 1
Approach 1: Detect Cycles with a HashSet
이게 첫번째 솔루션
class Solution:
def isHappy(self, n: int) -> bool:
def get_next(n):
total_sum = 0
while n > 0:
n, digit = divmod(n, 10)
total_sum += digit ** 2
return total_sum
seen = set()
while n != 1 and n not in seen:
seen.add(n)
n = get_next(n)
return n == 1
Approach 2: Floyd's Cycle-Finding Algorithm
두번째는 링크드리스트에서 fast와 slow이용해서 사이클 이용해서 보는건데, 이게 플로이드 알고리즘인줄은 처음알았네.
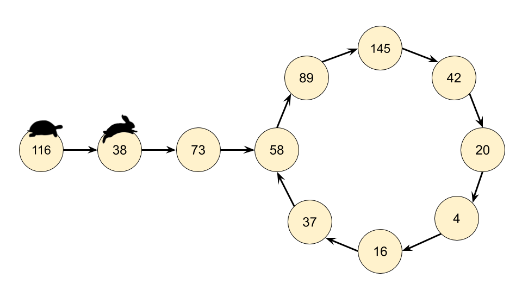
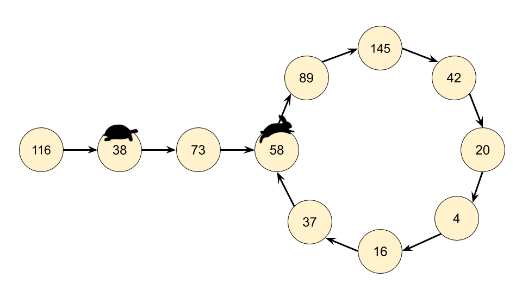
class Solution:
def isHappy(self, n: int) -> bool:
def get_next(n):
total_sum = 0
while n > 0:
n, digit = divmod(n, 10)
total_sum += digit ** 2
return total_sum
slow = n
fast = get_next(n)
while fast != 1 and slow != fast:
slow = get_next(slow)
fast = get_next(get_next(fast))
return fast == 1입력으로 1이 들어왔을때를 생각해보자. while의 fast != 1과 return fast == 1 을 주의해야한다.
172. Factorial Trailing Zeroes
leetcode.com/problems/factorial-trailing-zeroes/solution/
Given an integer n, return the number of trailing zeroes in n!.
Follow up: Could you write a solution that works in logarithmic time complexity?
Example 1:
Input: n = 3 Output: 0 Explanation: 3! = 6, no trailing zero.
Example 2:
Input: n = 5 Output: 1 Explanation: 5! = 120, one trailing zero.
Example 3:
Input: n = 0 Output: 0
Constraints:
- 0 <= n <= 104
Solution
Approach 1: Compute the Factorial
Intuition
This approach is too slow, but is a good starting point. You wouldn't implement it in an interview, although you might briefly describe it as a possible way of solving the problem.
The simplest way of solving this problem would be to compute n!n! and then count the number of zeroes on the end of it. Recall that factorials are calculated by multiplying all the numbers between 11 and nn. For example, 10! = 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 3,628,80010!=10⋅9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅1=3,628,800. Therefore, factorials can be calculated iteratively using the following algorithm.
define function factorial(n): n_factorial = 1 for i from 1 to n (inclusive): n_factorial = n_factorial * i return n_factorial
Recall that if a number has a zero on the end of it, then it is divisible by 1010. Dividing by 1010 will remove that zero, and shift all the other digits to the right by one place. We can, therefore, count the number of zeroes by repeatedly checking if the number is divisible by 1010, and if it is then dividing it by 1010. The number of divisions we're able to do is equal to the number of 0's on the end of it. This is the algorithm to count the zeroes (assuming x ≥ 1x≥1, which is fine for this problem, as factorials are always positive integers).
define function zero_count(x): zero_count = 0 while x is divisible by 10: zero_count += 1 x = x / 10 return zero_count
By putting these two functions together, we can count the number of zeroes on the end of n!n!.
Algorithm
For Java, we need to use BigInteger, because n!n! won't fit into a long for even moderately small values of nn.
class Solution:
def trailingZeroes(self, n: int) -> int:
n_fact = 1
for i in range(2, n + 1):
n_fact *= i
zero_cnt = 0
while n_fact % 10 == 0:
zero_cnt += 1
n_fact //= 10
return zero_cnt
Complexity Analysis
The math involved here is very advanced, however we don't need to be precise. We can get a reasonable approximation with a little mathematical reasoning. An interviewer probably won't expect you to calculate it exactly, or even derive the approximation as carefully as we have here. However, they might expect you to at least have some ideas and at least attempt to reason about it. Of course, if you've claimed to be an expert in algorithms analysis on your résumé/CV, then they might expect you to derive the entire thing! Our main reason for including it here is because it is a nice example of working with an algorithm that is mathematically challenging to analyse.
Let nn be the number we're taking the factorial of.
-
Time complexity : Worse than O(n ^ 2)O(n2).
Computing a factorial is repeated multiplication. Generally when we know multiplications are on numbers within a fixed bit-size (e.g. 32 bit or 64 bit ints), we treat them as O(1)O(1) operations. However, we can't do that here because the size of the numbers to be multiplied grow with the size of nn.
So, the first step here is to think about what the cost of multiplication might be, given that we can't assume it's O(1)O(1). A popular way people multiply two large numbers, that you probably learned in school, has a cost of O((\log \, x) \cdot (\log \, y))O((logx)⋅(logy)). We'll use that in our approximation.
Next, let's think about what multiplications we do when calculating n!n!. The first few multiplications would be as follows:
1 \cdot 2 = 21⋅2=2
2 \cdot 3 = 62⋅3=6
6 \cdot 4 = 246⋅4=24
24 \cdot 5 = 12024⋅5=120
120 \cdot 6 = 720120⋅6=720
......In terms of cost, these multiplications would have costs of:
\log \, 1 \cdot \log \, 2log1⋅log2
\log \, 2 \cdot \log \, 3log2⋅log3
\log \, 6 \cdot \log \, 4log6⋅log4
\log \, 24 \cdot \log \, 5log24⋅log5
\log \, 120 \cdot \log \, 6log120⋅log6
......Recognising that the first column are all logs of factorials, we can rewrite it as follows:
\log \, 1! \cdot \log \, 2log1!⋅log2
\log \, 2! \cdot \log \, 3log2!⋅log3
\log \, 3! \cdot \log \, 4log3!⋅log4
\log \, 4! \cdot \log \, 5log4!⋅log5
\log \, 5! \cdot \log \, 6log5!⋅log6
......See the pattern? Each line is of the form (\log \, k!) \cdot (\log \, k + 1)(logk!)⋅(logk+1). What would the last line be? Well, the last step in calculating a factorial is to multiply by nn. Therefore, the last line must be:
\log \, ((n - 1)!) \cdot \log \, (n)log((n−1)!)⋅log(n)
Because we're doing each of these multiplications one-by-one, we should add them to get the total time complexity. This gives us:
\log \, 1! \cdot \log \, 2 + \log \, 2! \cdot \log \, 3 + \log \, 3! \cdot \log \, 4 + \cdots + \log \, ((n - 2)!) \cdot \log \, (n - 1) + \log \, ((n - 1)!) \cdot \log \, nlog1!⋅log2+log2!⋅log3+log3!⋅log4+⋯+log((n−2)!)⋅log(n−1)+log((n−1)!)⋅logn
This sequence is quite complicated to add up; instead of trying to find an exact answer, we're going to now focus on a rough lower bound approximation by throwing away the less significant terms. While this is not something you'd do if we needed to find the exact time complexity, it will allow us to quickly see that the time complexity is "too big" for our purposes. Often finding lower (and upper) bounds is enough to decide whether or not an algorithm is worth using. This includes in interviews!
At this point, you'll ideally realise that the algorithm is worse than O(n)O(n), as we're adding nn terms. Given that the question asked us to come up with an algorithm that's no worse than O(\log \,n)O(logn), this is definitely not good enough. We're going to explore it a little further, but if you've understood up to this point, you're doing really well! The rest is optional.
Continuing on, notice that \log \, ((n - 1)!)log((n−1)!) is "a lot bigger" than \log\, nlogn. Therefore, we'll just drop all these parts, leaving the logs of factorials. This gives us:
\log \, 1! + \log \, 2! + \log , 3! + \cdots + \log \, ((n - 2)!) + \log \, ((n - 1)!)log1!+log2!+log,3!+⋯+log((n−2)!)+log((n−1)!)
The next part involves a log rule that you might or might not have heard of. It's definitely worth remembering if you haven't heard of it though, as it can be very useful.
O(\log \, n!) = O(n \, \log \, n)O(logn!)=O(nlogn)
So, let's rewrite the sequence using this rule.
1 \cdot \log \, 1 + 2 \cdot \log \, 2 + 3 \cdot \log \, 3 + \cdots + (n - 2) \cdot \log \, (n - 2) + (n - 1) \cdot \log \, (n - 1)1⋅log1+2⋅log2+3⋅log3+⋯+(n−2)⋅log(n−2)+(n−1)⋅log(n−1)
Like before, we'll just drop the "small" \loglog terms, and see what we're left with.
1 + 2 + 3 + ... + (n - 2) + (n - 1)1+2+3+...+(n−2)+(n−1)
This is a very familiar sequence, that you should be familiar with—it describes a cost of O(n^2)O(n2).
So, what can we conclude? Well, all the discarding of terms leaves us with a time complexity less than the real one. In other words, this factorial algorithm must be slower than O(n^2)O(n2).
O(n^2)O(n2) is definitely not good enough!
While this technique of throwing away terms here and there might seem a bit strange, it's very useful to make early decisions quickly, without needing to mess around with advanced math. Only once we had decided we were interested in looking at the algorithm further, would we try to come up with a more exact time complexity. And in this case, our lower bound was enough to convince us that it definitely isn't worth looking at!
The second part, counting the zeroes at the end, is insignificant compared to the first part. There are O(\log \, n!) = O(n \, \log \, n)O(logn!)=O(nlogn) digits, which is smaller than O(n^2)O(n2). Not to mention, only a few of them will be zeroes!
-
Space complexity : O(\log \, n!) = O(n \, \log \, n)O(logn!)=O(nlogn).
In order to store n!n!, we need O(\log \, n!)O(logn!) bits. As we saw above, this is the same as O(n \, \log \, n)O(nlogn).
Approach 2: Counting Factors of 5
Intuition
This approach is also too slow, however it's a likely step in the problem solving process for coming up with a logarithmic approach.
Instead of computing the factorial like in Approach 1, we can instead recognize that each 00 on the end of the factorial represents a multiplication by 1010.
So, how many times do we multiply by 1010 while calculating n!n! ? Well, to multiply two numbers, aa and bb, we're effectively multiplying all their factors together. For example, to do 42 \cdot 75 = 315042⋅75=3150, we can rewrite it as follows:
42 = 2 \cdot 3 \cdot 742=2⋅3⋅7
75 = 3 \cdot 5 \cdot 575=3⋅5⋅5
42 \cdot 75 = 2 \cdot 3 \cdot 7 \cdot 3 \cdot 5 \cdot 542⋅75=2⋅3⋅7⋅3⋅5⋅5
Now, in order to determine how many zeroes are on the end, we should look at how many complete pairs of 22 and 55 are among the factors. In the case of the example above, we have one 22 and two 55s, giving us one complete pair.
So, how does this relate to factorials? Well, in a factorial we're multiplying all the numbers between 11 and nn together, which is the same as multiplying all the factors of the numbers between 11 and nn.
For example, if n = 16n=16, we need to look at the factors of all the numbers between 11 and 1616. Keeping in mind that only 22s and 55s are of interest, we'll focus on those factors only. The numbers that contain a factor of 55 are {5, 10, 15}5,10,15. The numbers that contain a factor of 22 are {2, 4, 6, 8, 10, 12, 14, 16}2,4,6,8,10,12,14,16. Because there are only three numbers with a factor of 55, we can make three complete pairs, and therefore there must be three zeroes on the end of 16!16!.
Putting this into an algorithm, we get:
twos = 0 for i from 1 to n inclusive: if i is divisible by 2: twos += 1 fives = 0 for i from 1 to n inclusive: if i is divisible by 5: fives += 1 tens = min(fives, twos)
This gets us most of the way, but it doesn't consider numbers with more than one factor. For example, if i = 25, then we've only done fives += 1. However, we should've done fives += 2, because 2525 has two factors of 55.
Therefore, we need to count the 55 factors in each number. One way we can do this is by having a loop instead of the if statement, where each time we determine i has a 55 factor, we divide that 55 out. The loop will then repeat if there are further remaining 55 factors.
We can do that like this:
twos = 0 for i from 1 to n inclusive: remaining_i = i while remaining_i is divisible by 2: twos += 1 remaining_i = remaining_i / 2 fives = 0 for i from 1 to n inclusive: remaining_i = i while remaining_i is divisible by 5: fives += 1 remaining_i = remaining_i / 5 tens = min(twos, fives)
This gives us the right answer now. However, there are still some improvements we can make.
Firstly, we can notice that twos is always bigger than fives. Why? Well, every second number counts for a 22 factor, but only every fifth number counts as a 55 factor. Similarly every 4th number counts as an additional 22 factor, yet only every 25th number counts an additional 55 factor. This goes on and on for each power of 22 and 55. Here's a visualisation that illustrates how the density between 2 factors and 5 factors differs.
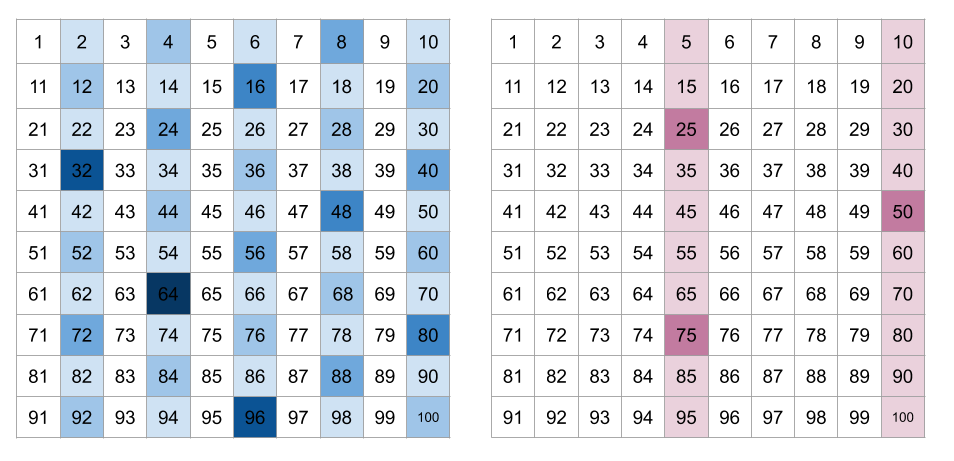
As such, we can simply remove the whole twos calculation, leaving us with:
fives = 0 for i from 1 to n inclusive: remaining_i = i while remaining_i is divisible by 5: fives += 1 remaining_i = remaining_i / 5 tens = fives
There is one final optimization we can do. In the above algorithm, we analyzed every number from 11 to nn. However, only 5, 10, 15, 20, 25, 30, ... etc5,10,15,20,25,30,...etc even have at least one factor of 55. So, instead of going up in steps of 11, we can go up in steps of 55. Making this modification gives us:
fives = 0 for i from 5 to n inclusive in steps of 5: remaining_i = i while remaining_i is divisible by 5: fives += 1 remaining_i = remaining_i / 5 tens = fives
Algorithm
Here's the algorithm as we designed it above.
Alternatively, instead of dividing by 55 each time, we can check each power of 55 to count how many times 55 is a factor. This works by checking if i is divisible by 55, then 2525, then 125125, etc. We stop when this number does not divide into i without leaving a remainder. The number of times we can do this is equivalent to the number of 55 factors in i.
Complexity Analysis
-
Time complexity : O(n)O(n).
In Approach 1, we couldn't treat division as O(1)O(1), because we went well outside the 32-bit integer range. In this Approach though, we stay within it, and so can treat division and multiplication as O(1)O(1).
To calculate the zero count, we loop through every fifth number from 55 to nn, this is O(n)O(n) steps (the \frac{1}{5}51 is treated as a constant).
At each step, while it might look like we do a, O(\log \, n)O(logn) operation to count the number of fives, it actually amortizes to O(1)O(1), because the vast majority of numbers checked only contain a single factor of 5. It can be proven that the total number of fives is less than \frac{2 \cdot n}{5}52⋅n.
So we get O(n) \cdot O(1) = O(n)O(n)⋅O(1)=O(n).
-
Space complexity : O(1)O(1).
We use only a fixed number of integer variables, therefore the space complexity is O(1)O(1).
Approach 3: Counting Factors of 5 Efficiently
Intuition
In Approach 2, we found a way to count the number of zeroes in the factorial, without actually calculating the factorial. This was by looping over each multiple of 55, from 55 up to nn, and counting how many factors of 55 were in each multiple of 55. We added all these counts together to get our final result.
However, Approach 2 was still too slow, both for practical means, and for the requirements of the question. To come up with a sufficient algorithm, we need to make one final observation. This observation will allow us to calculate our answer in logarithmic time.
Consider our simplified (but incorrect) algorithm that counted each multiple of 55. Recall that the reason it's incorrect is because it won't count both the 55 factors in numbers such as 2525, for example.
fives = 0 for i from 1 to n inclusive: if i is divisible by 5: fives += 1
If you think about this overly simplified algorithm a little, you might notice that this is simply an inefficient way of performing integer division for \frac{n}{5}5n. Why? Well, by counting the number of multiples of 55 up to nn, we're just counting how many 55s go into nn. That's the exact definition of integer division!
So, a way of simplifying the above algorithm is as follows.
fives = n / 5 tens = fives
So, how can we fix the "duplicate factors" problem? Observe that all numbers that have (at least) two factors of 55 are multiples of 2525. Like with the 55 factors, we can simply divide by 2525 to find how many multiples of 2525 are below nn. Also, notice that because we've already counted the multiples of 2525 in \frac{n}{5}5n once, we only need to count \frac{n}{25}25n extra factors of 55 (not 2 \cdot \frac{n}{25})2⋅25n)), as this is one extra for each multiple of 2525.
So combining this together we get:
fives = n / 5 + n / 25 tens = fives
We still aren't there yet though! What about the numbers which contain three factors of 55 (the multiples of 125125). We've only counted them twice! In order to get our final result, we'll need to add together all of \dfrac{n}{5}5n, \dfrac{n}{25}25n, \dfrac{n}{125}125n, \dfrac{n}{625}625n, and so on. This gives us:
fives = \dfrac{n}{5} + \dfrac{n}{25} + \dfrac{n}{125} + \dfrac{n}{625} + \dfrac{n}{3125} + \cdotsfives=5n+25n+125n+625n+3125n+⋯
This might look like it goes on forever, but it doesn't! Remember that we're using integer division. Eventually, the denominator will be larger than nn, and so all the terms from there will be 00. Therefore, we can stop once the term is 00.
For example with n = 12345n=12345 we get:
fives = \dfrac{12345}{5} + \dfrac{12345}{25} + \dfrac{12345}{125} + \dfrac{12345}{625} + \dfrac{12345}{3125} + \dfrac{12345}{16075} + \dfrac{12345}{80375} + \cdotsfives=512345+2512345+12512345+62512345+312512345+1607512345+8037512345+⋯
Which is equal to:
fives = 2469 + 493 + 98 + 19 + 3 + 0 + 0 + \cdots = 3082fives=2469+493+98+19+3+0+0+⋯=3082
In code, we can do this by looping over each power of 55, calculating how many times it divides into nn, and then adding that to a running fives count. Once we have a power of 55 that's bigger than nn, we stop and return the final value of fives.
fives = 0 power_of_5 = 5 while n >= power_of_5: fives += n / power_of_5 power_of_5 *= 5 tens = fives
Algorithm
An alternative way of writing this algorithm, is instead of trying each power of 55, we can instead divide nn itself by 55 each time. This works out the same because we wind up with the sequence:
fives = \dfrac{n}{5} + \dfrac{(\dfrac{n}{5})}{5} + \dfrac{(\dfrac{(\frac{n}{5})}{5})}{5} + \cdotsfives=5n+5(5n)+5(5(5n))+⋯
Notice that on the second step, we have \dfrac{(\frac{n}{5})}{5}5(5n). This is because the previous step divided nn itself by 55. And so on.
If you're familiar with the rules of fractions, you'll notice that \dfrac{(\frac{n}{5})}{5}5(5n) is just the same thing as \dfrac{n}{5 \cdot 5} = \frac{n}{25}5⋅5n=25n. This means the sequence is exactly the same as:
\dfrac{n}{5} + \dfrac{n}{25} + \dfrac{n}{125} + \cdots5n+25n+125n+⋯
So, this alternative way of writing the algorithm is equivalent.
Complexity Analysis
-
Time complexity : O(\log \, n)O(logn).
In this approach, we divide nn by each power of 55. By definition, there are \log_5nlog5n powers of 55 less-than-or-equal-to nn. Because the multiplications and divisions are within the 32-bit integer range, we treat these calculations as O(1)O(1). Therefore, we are doing \log_5 n \cdot O(1) = \log \, nlog5n⋅O(1)=logn operations (keeping in mind that \loglog bases are insignificant in big-oh notation).
-
Space complexity : O(1)O(1).
We use only a fixed number of integer variables, therefore the space complexity is O(1)O(1).
171. Excel Sheet Column Number
leetcode.com/problems/excel-sheet-column-number/
leetcode.com/problems/excel-sheet-column-number/solution/
171. Excel Sheet Column Number
Easy
1462187Add to ListShare
Given a column title as appear in an Excel sheet, return its corresponding column number.
For example:
A -> 1 B -> 2 C -> 3 ... Z -> 26 AA -> 27 AB -> 28 ...
Example 1:
Input: "A" Output: 1
Example 2:
Input: "AB" Output: 28
Example 3:
Input: "ZY" Output: 701
Constraints:
- 1 <= s.length <= 7
- s consists only of uppercase English letters.
- s is between "A" and "FXSHRXW".
Solution
This problem can be solved as if it is a problem of converting base-26 number system to base-10 number system.
Approach 1: Right to Left
Intuition
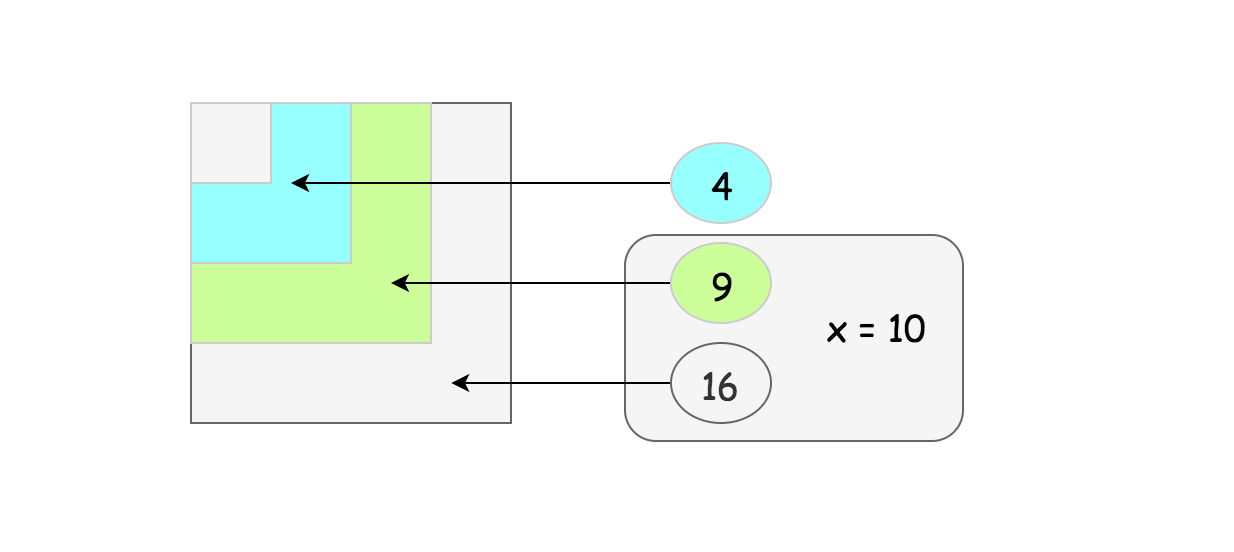
Let's tabulate the titles of an excel sheet in a table. There will be 26 rows in each column. Each cell in the table represents an excel sheet title.
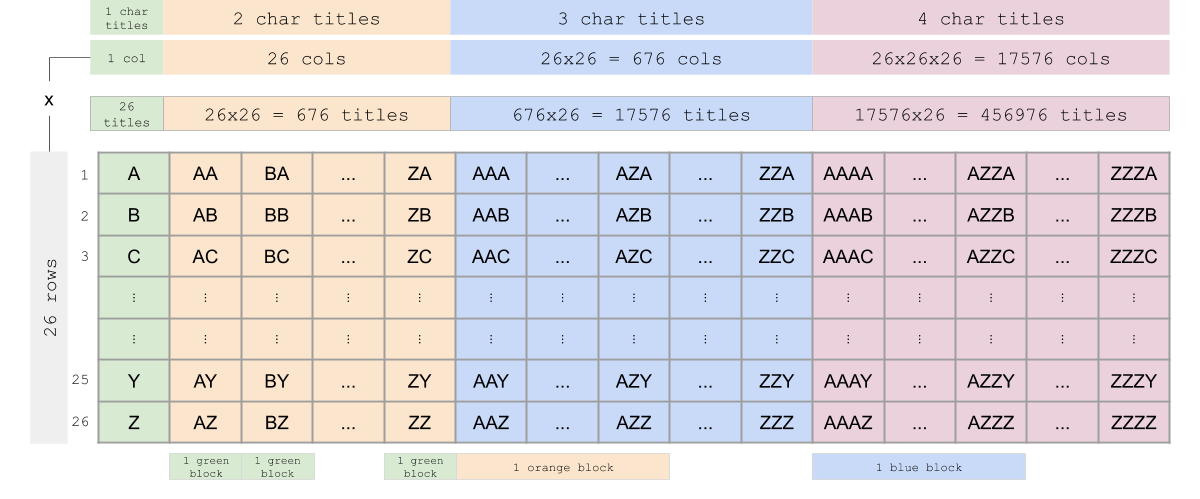
Pay attention to the "1 green block", "1 orange block" and "1 blue block" in the figure. These tell how bigger blocks are composed of smaller blocks. For example, blocks of 2-character titles are composed of 1-character blocks and blocks of 3-character titles are composed of 2-character blocks. This information is useful for finding a general pattern when calculating the values of titles.
Let's say we want to get the value of title AZZC. This can be broken down as 'A***' + 'Z**' + 'Z*' + 'C'. Here, the *s represent smaller blocks. * means a block of 1-character titles. ** means a block of 2-character titles. There are 261 titles in a block of 1-character titles. There are 262 titles in a block of 2-character titles.
Scanning AZZC from right to left while accumulating results:
- First, ask the question, what the value of 'C' is:
- 'C' = 3 x 260 = 3 x 1 = 3
- result = 0 + 3 = 3
- Then, ask the question, what the value of 'Z*' is:
- 'Z*' = 26 x 261 = 26 x 26 = 676
- result = 3 + 676 = 679
- Then, ask the question, what the value of 'Z**' is:
- 'Z**' = 26 x 262 = 26 x 676 = 17576
- result = 679 + 17576 = 18255
- Finally, ask the question, what the value of 'A***' is:
- 'A***' = 1 x 263 = 1 x 17576 = 17576
- result = 18255 + 17576 = 35831
Algorithm
- To get indices of alphabets, create a mapping of alphabets and their corresponding values. (1-indexed)
- Initialize an accumulator variable result.
- Starting from right to left, calculate the value of the character associated with its position and add it to result.
Implementation
내가 짠 코드 답이랑 조금 다른
해답: alpha_map = {chr(i + 65): i + 1 for i in range(26)}
class Solution:
def titleToNumber(self, s: str) -> int:
result = 0
n = len(s)
for i in range(n):
cur_char = s[n-1-i]
result += (ord(cur_char)-ord('A')+1)*(26**i)
return result
Complexity Analysis
-
Time complexity : O(N)O(N) where NN is the number of characters in the input string.
-
Space complexity : O(1)O(1). Even though we have an alphabet to index mapping, it is always constant.
Approach 2: Left to Right
아직못봄
Intuition
Rather than scanning from right to left as described in Approach 1, we can also scan the title from left to right.
For example, if we want to get the decimal value of string "1337", we can iteratively find the result by scanning the string from left to right as follows:
- '1' = 1
- '13' = (1 x 10) + 3 = 13
- '133' = (13 x 10) + 3 = 133
- '1337' = (133 x 10) + 7 = 1337
Instead of base-10, we are dealing with base-26 number system. Based on the same idea, we can just replace 10s with 26s and convert alphabets to numbers.
For a title "LEET":
- L = 12
- E = (12 x 26) + 5 = 317
- E = (317 x 26) + 5 = 8247
- T = (8247 x 26) + 20 = 214442
In Approach 1, we have built a mapping of alphabets to numbers. There is another way to get the number value of a character without building an alphabet mapping. You can do this by converting a character to its ASCII value and subtracting ASCII value of character 'A' from that value. By doing so, you will get results from 0 (for A) to 25 (for Z). Since we are indexing from 1, we can just add 1 up to the result. This eliminates a loop where you create an alphabet to number mapping which was done in Approach 1.
Implementation
Complexity Analysis
-
Time complexity : O(N)O(N) where NN is the number of characters in the input string.
-
Space complexity : O(1)O(1).
관련문제: leetcode.com/problems/excel-sheet-column-title/
class Solution:
def convertToTitle(self, n: int) -> str:
title = ""
while n > 0:
n, digit = divmod(n, 26)
if digit > 0:
title += chr(ord('A')-1 + digit)
elif digit == 0:
title += 'Z'
n -= 1
return title[::-1]ord, chr, reverse[::-1]
내코드는 이거고 result코드는 아래에...
class Solution:
def convertToTitle(self, n: int) -> str:
def helper(n):
print(n)
if n == 0:
return ""
end = (n % 26)
if end == 0:
end = 26
letter = chr(64 + end)
rest = helper((n - end) // 26)
return rest + letter
return helper(n)class Solution:
def convertToTitle(self, n: int) -> str:
res = ""
while n:
res += chr(ord("A") + (n - 1) % 26)
n = (n - 1) // 26
return res[::-1]
관련문제 구글기출
leetcode.com/problems/maximum-of-absolute-value-expression/
leetcode.com/problems/powx-n/solution/
69. Sqrt(x)
leetcode.com/problems/sqrtx/solution/
태그가 math랑 binary search 다.
Given a non-negative integer x, compute and return the square root of x.
Since the return type is an integer, the decimal digits are truncated, and only the integer part of the result is returned.
Example 1:
Input: x = 4 Output: 2
Example 2:
Input: x = 8 Output: 2 Explanation: The square root of 8 is 2.82842..., and since the decimal part is truncated, 2 is returned.
Constraints:
- 0 <= x <= 231 - 1
Try exploring all integers. (Credits: @annujoshi)
Use the sorted property of integers to reduced the search space. (Credits: @annujoshi)
Solution
Integer Square Root
The value aa we're supposed to compute could be defined as a^2 \le x < (a + 1)^2a2≤x<(a+1)2. It is called integer square root. From geometrical points of view, it's the side of the largest integer-side square with a surface less than x.
Approach 1: Pocket Calculator Algorithm
Before going to the serious stuff, let's first have some fun and implement the algorithm used by the pocket calculators.
Usually a pocket calculator computes well exponential functions and natural logarithms by having logarithm tables hardcoded or by the other means. Hence the idea is to reduce the square root computation to these two algorithms as well
\sqrt{x} = e^{\frac{1}{2} \log x}x=e21logx
That's some sort of cheat because of non-elementary function usage but it's how that actually works in a real life.

Implementation
Complexity Analysis
-
Time complexity : \mathcal{O}(1)O(1).
-
Space complexity : \mathcal{O}(1)O(1).
Approach 2: Binary Search
Intuition
Let's go back to the interview context. For x \ge 2x≥2 the square root is always smaller than x / 2x/2 and larger than 0 : 0 < a < x / 20<a<x/2.
Since aa is an integer, the problem goes down to the iteration over the sorted set of integer numbers. Here the binary search enters the scene.
Algorithm
-
If x < 2, return x.
-
Set the left boundary to 2, and the right boundary to x / 2.
-
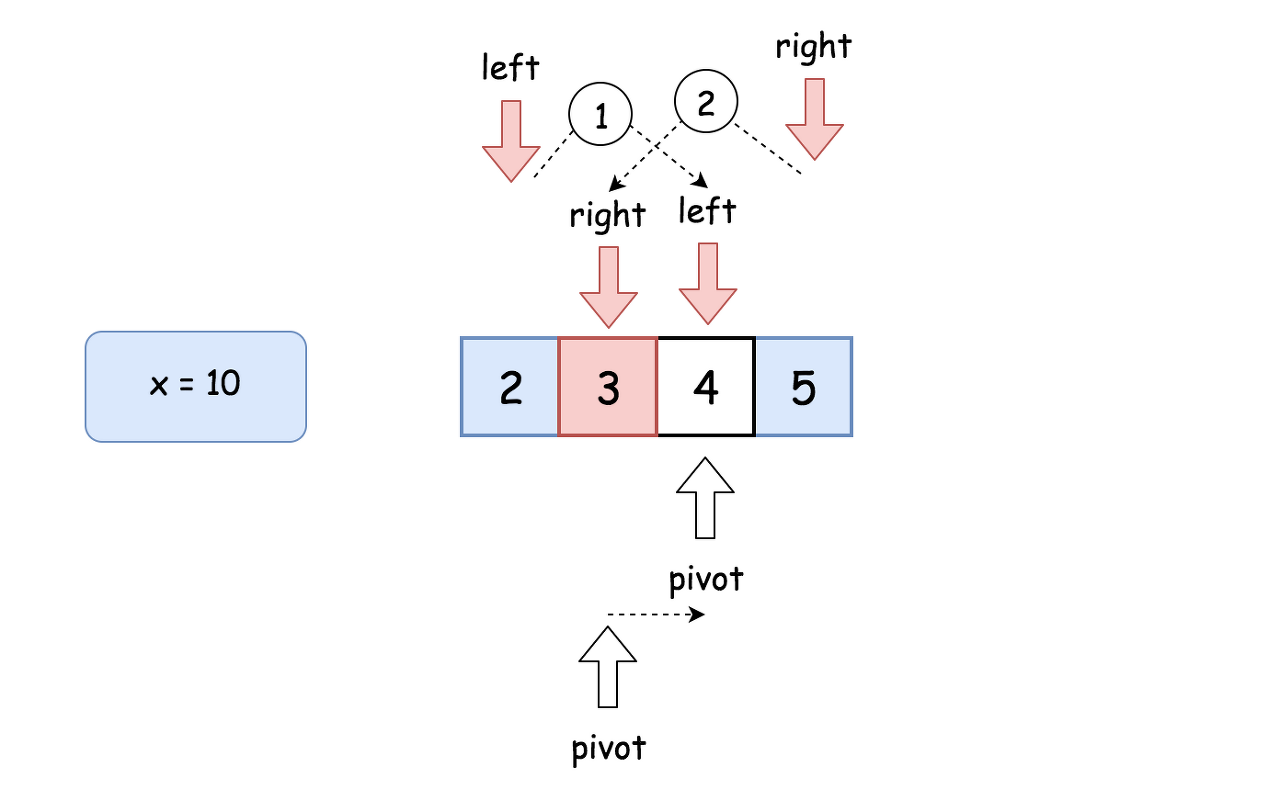
While left <= right:
-
Take num = (left + right) / 2 as a guess. Compute num * num and compare it with x:
-
If num * num > x, move the right boundary right = pivot -1
-
Else, if num * num < x, move the left boundary left = pivot + 1
-
Otherwise num * num == x, the integer square root is here, let's return it
-
-
-
Return right
Implementation
Complexity Analysis
-
Time complexity : \mathcal{O}(\log N)O(logN).
Let's compute time complexity with the help of master theorem T(N) = aT\left(\frac{N}{b}\right) + \Theta(N^d)T(N)=aT(bN)+Θ(Nd). The equation represents dividing the problem up into aa subproblems of size \frac{N}{b}bN in \Theta(N^d)Θ(Nd) time. Here at step there is only one subproblem a = 1, its size is a half of the initial problem b = 2, and all this happens in a constant time d = 0. That means that \log_b{a} = dlogba=d and hence we're dealing with case 2 that results in \mathcal{O}(n^{\log_b{a}} \log^{d + 1} N)O(nlogbalogd+1N) = \mathcal{O}(\log N)O(logN) time complexity.
-
Space complexity : \mathcal{O}(1)O(1).
Approach 3: Recursion + Bit Shifts
Intuition
Let's use recursion. Bases cases are \sqrt{x} = xx=x for x < 2x<2. Now the idea is to decrease xx recursively at each step to go down to the base cases.
How to go down?
For example, let's notice that \sqrt{x} = 2 \times \sqrt{\frac{x}{4}}x=2×4x, and hence square root could be computed recursively as
\textrm{mySqrt}(x) = 2 \times \textrm{mySqrt}\left(\frac{x}{4}\right)mySqrt(x)=2×mySqrt(4x)
One could already stop here, but let's use left and right shifts, which are quite fast manipulations with bits
x << y \qquad \textrm{that means} \qquad x \times 2^yx<<ythat meansx×2y
x >> y \qquad \textrm{that means} \qquad \frac{x}{2^y}x>>ythat means2yx
That means one could rewrite the recursion above as
\textrm{mySqrt}(x) = \textrm{mySqrt}(x >> 2) << 1mySqrt(x)=mySqrt(x>>2)<<1
in order to fasten up the computations.
Implementation
Complexity Analysis
-
Time complexity : \mathcal{O}(\log N)O(logN).
Let's compute time complexity with the help of master theorem T(N) = aT\left(\frac{N}{b}\right) + \Theta(N^d)T(N)=aT(bN)+Θ(Nd). The equation represents dividing the problem up into aa subproblems of size \frac{N}{b}bN in \Theta(N^d)Θ(Nd) time. Here at step there is only one subproblem a = 1, its size is a half of the initial problem b = 2, and all this happens in a constant time d = 0. That means that \log_b{a} = dlogba=d and hence we're dealing with case 2 that results in \mathcal{O}(n^{\log_b{a}} \log^{d + 1} N)O(nlogbalogd+1N) = \mathcal{O}(\log N)O(logN) time complexity.
-
Space complexity : \mathcal{O}(\log N)O(logN) to keep the recursion stack.
Approach 4: Newton's Method
Intuition
One of the best and widely used methods to compute sqrt is Newton's Method. Here we'll implement the version without the seed trimming to keep things simple. However, seed trimming is a bit of math and lot of fun, so here is a link if you'd like to dive in.
Let's keep the mathematical proofs outside of the article and just use the textbook fact that the set
x_{k + 1} = \frac{1}{2}\left[x_k + \frac{x}{x_k}\right]xk+1=21[xk+xkx]
converges to \sqrt{x}x if x_0 = xx0=x. Then the things are straightforward: define that error should be less than 1 and proceed iteratively.
Implementation
Complexity Analysis
-
Time complexity : \mathcal{O}(\log N)O(logN) since the set converges quadratically.
-
Space complexity : \mathcal{O}(1)O(1).
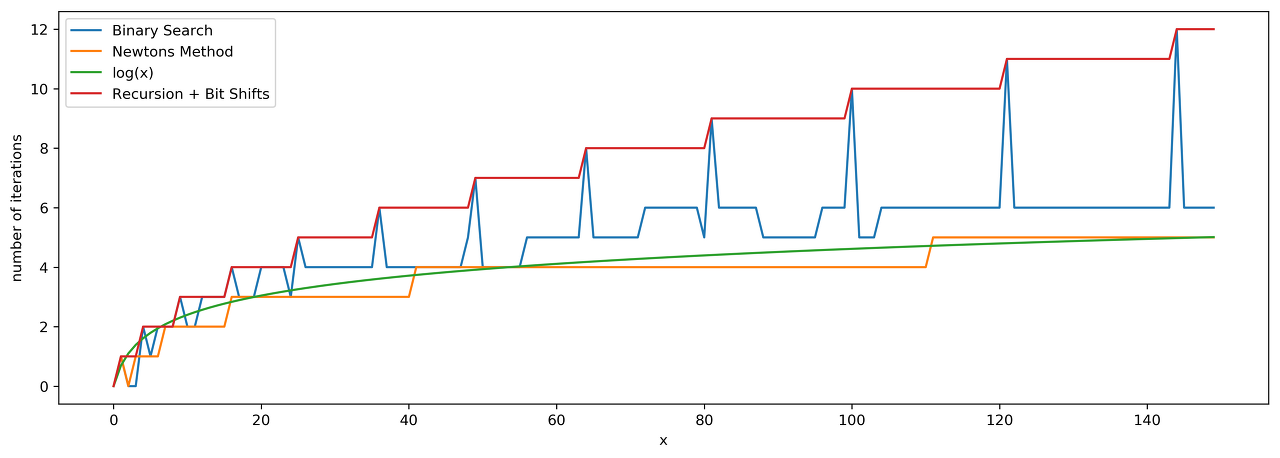
Compare Approaches 2, 3 and 4
Here we have three algorithms with a time performance \mathcal{O}(\log N)O(logN), and it's a bit confusing.
Which one is performing less iterations?
Let's run tests for the range of x in order to check that. Here are the results. The best one is Newton's method.
leetcode.com/problems/divide-two-integers/solution/
leetcode.com/problems/fraction-to-recurring-decimal/solution/





