BST Successor Search

BST Successor Search

In a Binary Search Tree (BST), an Inorder Successor of a node is defined as the node with the smallest key greater than the key of the input node (see examples below). Given a node inputNode in a BST, you’re asked to write a function findInOrderSuccessor that returns the Inorder Successor of inputNode. If inputNode has no Inorder Successor, return null.

Explain your solution and analyze its time and space complexities.

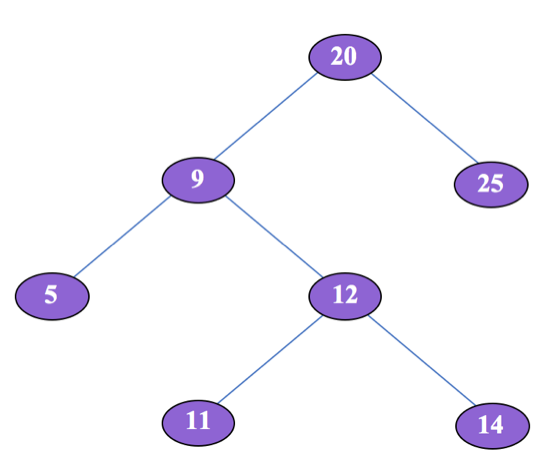
In this diagram, the inorder successor of 9 is 11 and the inorder successor of 14 is 20.

Example:

In the diagram above, for inputNode whose key = 11

Your function would return:

The Inorder Successor node whose key = 12

Constraints:

• [time limit] 5000ms
• [input] Node inputNode
• [output] Node

 

 

 

BST Successor Search

• First, make sure your peer understands the question.
• If you or your peer have a hard time understanding how to go about solving this problem, or could use a reminder of how BSTs work, take this interactive BST application for a spin.
• If your peer is still stuck, ask them to look again at the examples provided above (in the diagram caption and “For example”) and see if based on these examples they can discern the two different cases in which a node is an Inorder Successor of a given input node.
• Your peer may suggest another approach and that is to start searching from the root and traversing the tree in a binary search manner. While correct, ask them to come up with a solution that doesn’t require the root.

 

 

 

 

BST Successor Search

Let’s denote the Inorder Successor of inputNode as successorNode. To arrive to the solution, we distinguish between two cases:

• inputNode has a right child. In this case successorNode would be the node with the minimum key in inputNode's right subtree.

• inputNode doesn’t have a right child. In this case successorNode would be one of inputNode's ancestors. More specifically, within inputNode's ancestor chain (starting from inputNode all the way up to the root), successorNode is the first parent that has a left child in that chain.

If inputNode doesn’t have a right child and all of its ancestors are right children to their parents, inputNode doesn’t have a successor (successorNode would be null).

So why is this always true? Well, if inputNode was inserted to the tree prior to successorNode, then since successorNode.key is greater than inputNode.key, but also smaller than all other keys greater than successorNode.key, successorNode has to be in inputNode's right subtree.

Now, if inputNode was inserted to the tree after successorNode was, then since inputNode.key is smaller than successorNode.key, but also larger than all other keys smaller than successorNode.key, inputNode has to be in successorNode's left subtree.

Pseudocode:

function findInOrderSuccessor(inputNode): if (inputNode.right != null): # return the node with minimum key in the right subtree return findMinKeyWithinTree(inputNode.right) ancestor = inputNode.parent child = inputNode # travel up using the parent pointer until you see # a node which is the left child of its parent. The parent # of such a node is successorNode. while (ancestor != null AND child == ancestor.right): child = ancestor ancestor = child.parent return ancestor function findMinKeyWithinTree(inputNode): while (inputNode.left != null): inputNode = inputNode.left return inputNode

Time Complexity: in both cases where either inputNode has a right child or doesn’t have one, we are visiting only O(H) number of nodes, where H is the height of the BST. For a balanced BST, since H = log(N), where N is the number of nodes in the BST, the time complexity is O(log(N)). For an unbalanced BST, the time complexity is O(N).

Space Complexity: throughout the entire algorithm we used only a constant amount of space, hence the space complexity is O(1).

 

 

    Node findInOrderSuccessor(Node inputNode) {
      if(inputNode.right != null) {
        return findMinKeyWithinTree(inputNode);
      }
      
      Node ancestor = inputNode.parent;
      Node child = inputNode;
      
      while(ancestor != null && child == ancestor.right) {
        child = ancestor;
        ancestor = child.parent;
      }

      return ancestor;
    }
    
    Node findMinKeyWithinTree(Node node) {
      while(node.left != null) {
        node = node.left;
      }
      return node;
    }