485. Max Consecutive Ones
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int maxHere = 0, max = 0;
for (int n : nums)
max = Math.max(max, maxHere = n == 0 ? 0 : maxHere + 1);
return max;
}
}Max Consecutive Ones
Solution
Given a binary array, find the maximum number of consecutive 1s in this array.
Example 1:
Input: [1,1,0,1,1,1] Output: 3 Explanation: The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
Note:
- The input array will only contain 0 and 1.
- The length of input array is a positive integer and will not exceed 10,000
Hide Hint #1
You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window. How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size.
최대 연속 사람
해결책
이진 배열이 주어지면이 배열에서 연속되는 1의 최대 수를 찾습니다.
예 1 :
입력 : [1,1,0,1,1,1] 출력 : 3 설명 : 처음 두 자리 또는 마지막 세 자리는 연속 된 1입니다. 연속 1의 최대 수는 3입니다.
노트 :
입력 배열에는 0과 1 만 포함됩니다.
입력 배열의 길이는 양의 정수이며 10,000을 초과하지 않습니다.
힌트 # 1 숨기기
창에 관한 한 두 가지를 생각해야합니다. 하나는 창의 시작점입니다. 1의 새 창이 시작되었음을 어떻게 감지합니까? 다음 부분은이 창의 끝점을 감지하는 것입니다. 기존 창의 끝점을 어떻게 감지합니까? 이 두 가지를 알아 내면 연속 된 창을 감지 할 수 있습니다. 그 후 남은 것은 가장 긴 창을 찾아 크기를 반환하는 것입니다.
문제를 잘 안읽어서 이상한 코드를 짰다.. 반성하자..
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int ans = 0;
int temp_max = 0;
for(int i = 0; i < nums.length-1; ++i) {
if(nums[i] == nums[i+1]) {
if(temp_max == 0) ++temp_max;
++temp_max;
if(ans < temp_max)
ans = temp_max;
}
else {
temp_max = 0;
}
}
return ans;
}
}
내꺼
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int ans = 0;
int temp_max = 0;
for(int i = 0; i < nums.length; ++i) {
if(nums[i] == 1) {
++temp_max;
ans = (ans < temp_max)? temp_max : ans;
}
else {
temp_max = 0;
}
}
return ans;
}
}
Solution
The constraints for this problem make it easy
to understand that it can be done in one iteration.
The length of input array is a positive integer and will not exceed 10,000
How else do you expect to find the number of 1's in an array without making at least one pass through the array. So let's look at the solution.
Approach: One pass
Intuition
The intuition is pretty simple. We keep a count of the number of 1's encountered. And reset the count whenever we encounter anything other than 1 (which is 0 for this problem). Thus, maintaining count of 1's between zeros or rather maintaining counts of contiguous 1's. It's the same as keeping a track of the number of hours of sleep you had, without waking up in between.
Algorithm
-
Maintain a counter for the number of 1's.
-
Increment the counter by 1, whenever you encounter a 1.
-
Whenever you encounter a 0
a. Use the current count of 1's to find the maximum contiguous 1's till now.
b. Afterwards, reset the counter for 1's to 0.
-
Return the maximum in the end.
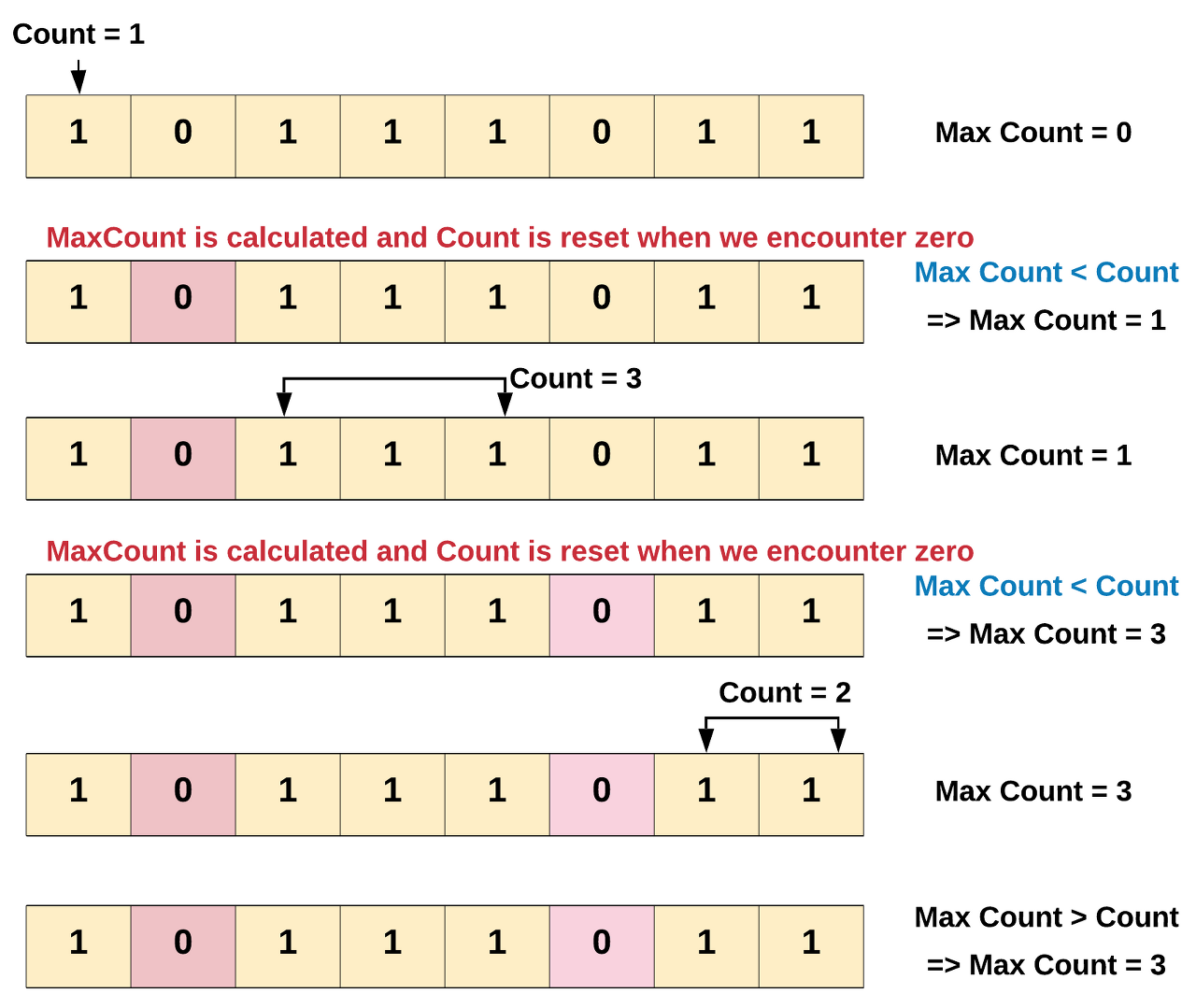
In the above diagram we found out that the maximum number of consecutive 1's is 3. There were two breaks in the count we encountered while iterating the array. Every time the break i.e. 0 was encountered we had to reset the count of 1 to zero.
Note - The maximum count is only calculated when we encounter a break i.e. 0, since thats where a subarray of 1's ends.
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int count = 0;
int maxCount = 0;
for(int i = 0; i < nums.length; i++) {
if(nums[i] == 1) {
// Increment the count of 1's by one.
count += 1;
} else {
// Find the maximum till now.
maxCount = Math.max(maxCount, count);
// Reset count of 1.
count = 0;
}
}
return Math.max(maxCount, count);
}
}
Complexity Analysis
-
Time Complexity: O(N)O(N), where NN is the number of elements in the array.
-
Space Complexity: O(1)O(1). We do not use any extra space.
Follow up:
You can also try something fancy one liner solution as shared by Stefan Pochmann.
def findMaxConsecutiveOnes(self, nums): return max(map(len, ''.join(map(str, nums)).split('0')))
Note, how he converts the list into a string, using map and join functions. Then, splits the resultant string on 0. The maximum of the lengths of these list of strings of 1's is the answer we are looking for.
솔루션이 내꺼랑 좀 다르고, 결과에 있는 코드들도 참고할만한것 같다.
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int max=0;
int current=0;
for(int i=0;i<nums.length;i++){
if(nums[i]==1){
current++;
}
else{
if(current>max){
max=current;
}
if(max>nums.length/2){
return max;
}
current=0;
}
}
return Math.max(current,max);
}
}
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
if (nums.length == 0)
return -1;
boolean any_ones = Arrays.stream(nums).anyMatch(x -> x == 1);
if (!any_ones) {
return 0;
}
int max_length = Integer.MIN_VALUE;
int i = 0;
while (i < nums.length) {
if (nums[i] == 1) {
int j = i + 1;
while (j < nums.length && nums[j] == 1) {
j++;
}
max_length = Math.max(max_length, j - i);
i = j;
} else {
while (i < nums.length && nums[i] == 0) {
i++;
}
}
}
return max_length;
}
}
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
ArrayList out = new ArrayList();
int count = 0;
for (int i = 0; i<nums.length; i++) {
if (nums[i] == 1) {
count = count + 1;
}
else {
out.add(count);
count = 0;
}
}
out.add(count);
return (int) Collections.max(out);
}
}





