1492. The kth Factor of n

leetcode.com/problems/the-kth-factor-of-n/

The kth Factor of n - LeetCode

Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.

leetcode.com

금요일이라고 쉬운문제인건가 싶었지만, 그렇지 않았음

In this article, we consider three solutions.

Approach 1:

Brute Force, \mathcal{O}(N). One could iterate from 1 to N, figure out all divisors in a linear time, and then return the kth one.

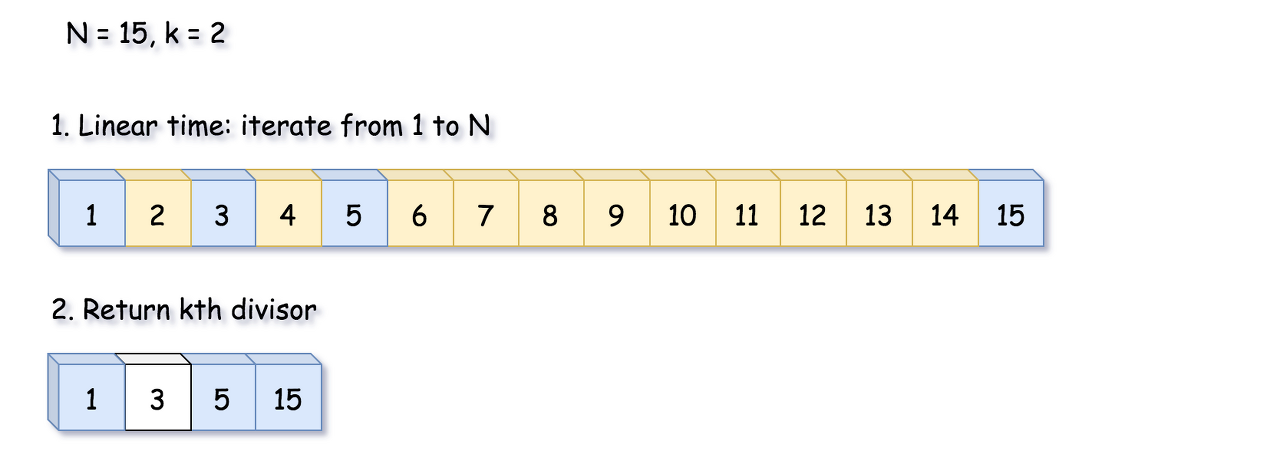
Fig. 1. Approach 1: Brute Force, \mathcal{O}(N). The idea is to iterate from 1 to N to figure out all divisors.

The implementation of the next two approaches is based on the same idea.

The divisors are paired, i.e., if i is a divisor of N, then N / i is a divisor of N, too. That means it's enough to iterate up to \sqrt{N}.

Fig. 2. Iterate from 1 to \sqrt{N} is enough.

Approach 2:

Heap, \mathcal{O}(\sqrt{N} \log k). The idea is to iterate from 1 to \sqrt{N}, and push each divisor and its pair into max heap of size k.

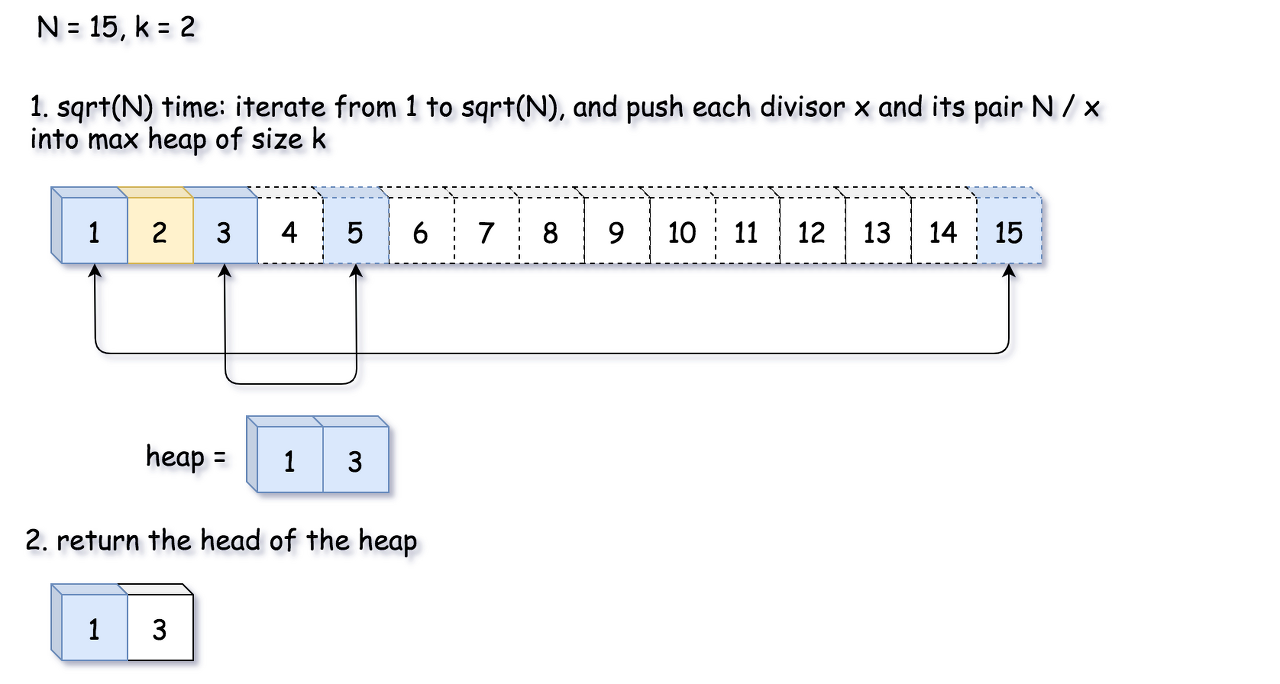
Fig 3. Approach 2. Heap: Iterate from 1 to \sqrt{N} is enough, and push each divisor and its pair into max heap.

Approach 3:

Math, \mathcal{O}(\sqrt{N}). As in Approach 2, let's iterate up to \sqrt{N}, and decrease k by one at each step. If k drops down to zero during the iterations - the kth divisor is here. Otherwise, the kth divisor is the paired one and could be found as N / divisors[len(divisors) - k].

Fig. 4. Approach 3. Math: Iterate from 1 to \sqrt{N} is enough.

Approach 1:

Brute Force, time

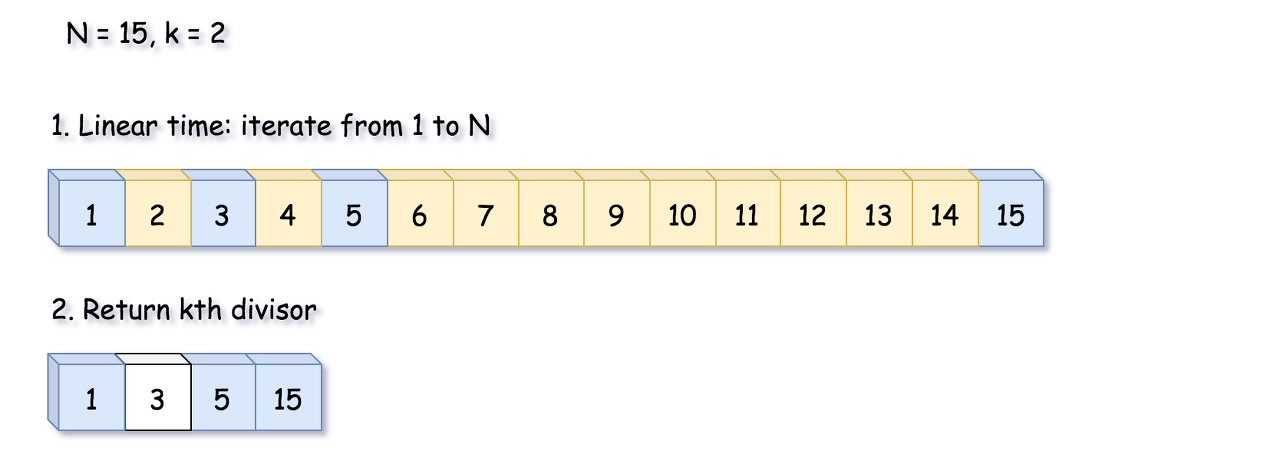
Fig. 5. Approach 1: Brute Force.

Algorithm

Iterate by x from 1 to N / 2:
- If x is a divisor of N, decrease k by one. Return x if k == 0.
Return N if k == 1 and -1 otherwise.

class Solution {
    public int kthFactor(int n, int k) {
        for (int x = 1; x < n / 2 + 1; ++x) {
            if (n % x == 0) {
                --k;
                if (k == 0) {
                    return x;    
                }    
            }    
        }
        
        return k == 1 ? n : -1;
    }
}

이 코드와 위의 코드는 많은 차이가 있다.

n까지 모두 도는게, 숫자가 크면 시간이 오래 걸린다. n/2+1 까지만 돌아야함.

그리고 위의 코드는 n까지 돌지 않기 때문에, 마지막 리턴에서 아래에서 n에 대한것을 따로 처리해주어야한다.

class Solution {
    public int kthFactor(int n, int k) {
        for(int i = 1; i <= n; i++) {
            if(n%i == 0) {
                k--;
                if(k==0) {
                    return i;
                }
            }
        }
        return -1;
    }
}

Implementation

Complexity Analysis

Time Complexity: to iterate from 1 to N.
Space Complexity: , since we don't allocate any additional data structures.

Approach 2:

Heap, \mathcal{O}(\sqrt{N} \times \log{k}) time

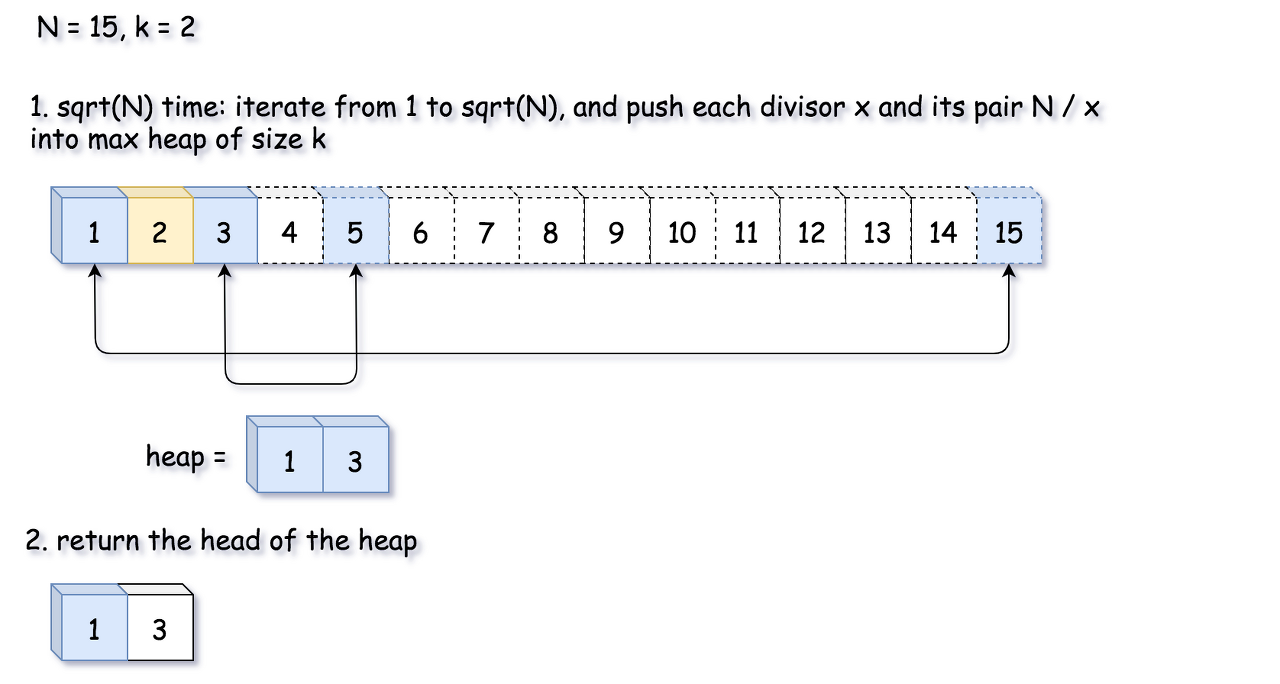
Fig 6. Approach 2: Heap.

Algorithm

Initialize max heap. Use PriorityQueue in Java and heap in Python. heap is a min-heap. Hence, to implement max heap, change the sign of divisor before pushing it into the heap.
Iterate by x from 1 to \sqrt{N}:
- If x is a divisor of N, push x and its pair divisor n / x into the heap of size k.
Return the head of the heap if its size is equal to k and -1 otherwise.

힙에다가 원소를 추가할 때, k개수보다 넘는것은 뒤에서 부터 삭제한다.

class Solution {
    // max heap -> to keep max element always on top
    Queue<Integer> heap = new PriorityQueue<>((o1, o2) -> o2 - o1);
    
    // push into heap
    // by limiting size of heap to k
    public void heappushK(int x, int k) {
        heap.add(x);
        if (heap.size() > k) {
            heap.remove();    
        }
    }
    
    public int kthFactor(int n, int k) {
        int sqrtN = (int) Math.sqrt(n);
        for (int x = 1; x < sqrtN + 1; ++x) {
            if (n % x == 0) {
                heappushK(x, k);
                if (x != n / x) {
                    heappushK(n / x, k);    
                }    
            }    
        }
                
        return k == heap.size() ? heap.poll() : -1;
    }
}

Implementation

Complexity Analysis

Time Complexity: \mathcal{O}(\sqrt{N} \times \log k).
- sqrt(N) x logK : 힙 만들때 걸리는 시간이다.
Space Complexity: \mathcal{O}(\min(k, \sqrt{N})) to keep the heap of size k.

Approach 3:

Math, \mathcal{O}(\sqrt{N}) time

Fig. 7. Approach 3: Math.

Algorithm

Initialize a list divisors to store the divisors.
Iterate by x from 1 to \sqrt{N}:
- If x is a divisor of N, decrease k by one. Return x if k == 0.
We're here because the kth divisor is not yet found. Although divisors already contains all "independent" divisors. All other divisors are "paired" ones, i.e, the kth divisor could be computed as N / divisors[len(divisors) - k].

But before that, we need a small correction for the case when N is a perfect square. In that case, the divisor list contains a duplicate because \sqrt{N} appears two times. To skip it, we have to increase k by one.
Return N / divisors[len(divisors) - k] if k <= len(divisors) and -1 otherwise.

class Solution {
    public int kthFactor(int n, int k) {
        List<Integer> divisors = new ArrayList();
        int sqrtN = (int) Math.sqrt(n);
        for (int x = 1; x < sqrtN + 1; ++x) {
            if (n % x == 0) {
                --k;
                divisors.add(x);
                if (k == 0) {
                    return x;    
                }    
            }    
        }
        
        // If n is a perfect square
        // we have to skip the duplicate 
        // in the divisor list
        if (sqrtN * sqrtN == n) {
            ++k;    
        }
                
        int nDiv = divisors.size();
        return (k <= nDiv) ? n / divisors.get(nDiv - k) : -1;
    }
}

Implementation

Complexity Analysis