382. Linked List Random Node - Reservoir Sampling

www.geeksforgeeks.org/reservoir-sampling/

Reservoir Sampling - GeeksforGeeks

 

---

 

leetcode.com/problems/linked-list-random-node/

Linked List Random Node - LeetCode

 

 

 

Given a singly linked list, return a random node's value from the linked list. Each node must have the same probability of being chosen.
Follow up:What if the linked list is extremely large and its length is unknown to you? Could you solve this efficiently without using extra space?
단일 링크 리스트가 주어지면 링크된 리스트에서 랜덤 노드 값을 반환합니다. 각 노드는 선택될 확률이 같아야 합니다. 후속 조치: 링크된 목록이 매우 크고 길이가 알려지지 않은 경우? 여분의 공간을 사용하지 않고도 이 문제를 효율적으로 해결할 수 있나요?

// Init a singly linked list [1,2,3].
ListNode head = new ListNode(1);
head.next = new ListNode(2);
head.next.next = new ListNode(3);
Solution solution = new Solution(head);

// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
solution.getRandom();

 

 

 

Overview

The solution for this problem could be as simple as it sounds, i.e. sampling from a linked list. However, with the constraint raised by the follow-up question, it becomes more interesting.

As a spoiler alert, in this article we will present an algorithm called Reservoir sampling which is a family of randomized algorithms for sampling from a population of unknown size.

 

개요 

이 문제에 대한 해결책은 들리는 것처럼 간단할 수 있다. 즉, 링크된 목록에서 샘플링하는 것이다. 그러나 후속문제로 인해 제기된 제약으로 더욱 흥미로워진다.  스포일러 경보로서, 이 글에서 우리는 알려지지 않은 크기의 집단으로부터 샘플링을 위한 무작위 알고리즘의 계열인 저수지 샘플링이라는 알고리즘을 제시할 것이다.

 

---

Approach 1: Fixed-Range Sampling

Intuition

First of all, let us talk about the elephant in the room. Yes, the problem could be as simple as choosing a random sample from a list, which in our case happens to be a linked list.

If we are given an array or a linked list with a known size, then it would be a no brainer to solve the problem.

One of the most intuitive ideas would be that we convert the linked list into an array. With the array, we would know its size and moreover we could have an instant access to its elements.

Algorithm

We are asked to implement two interfaces in the object, namely the init(head) and getRandom() functions.

The init(head) function would be invoked once when we construct the object. Within which, intuitively we could convert the given linked list into an array for later reuse.

Concerning the getRandom() function, with the linked list converted into an array, we could simply sample from this array.

 

접근법 1: 고정 범위 샘플링직감우선, 방에 있는 코끼리에 대해 이야기해보자. 그렇다, 문제는 리스트에서 무작위 샘플을 선택하는 것만큼 간단할 수 있다. 우리의 경우는 링크된 리스트가 된다.만약 우리에게 알려진 크기의 배열이나 링크된 목록이 주어진다면, 문제를 해결하는 것은 현명하지 못한 일일 것이다.가장 직관적인 아이디어 중 하나는 링크된 목록을 배열로 변환하는 것이다. 배열로, 우리는 그것의 크기를 알 수 있었고, 게다가 우리는 그것의 요소들에 즉각적으로 접근할 수 있었다.알고리즘.개체에서 init(head)와 getRandom() 함수라는 두 가지 인터페이스를 구현하도록 요청받았다.초기화(헤드) 함수는 우리가 객체를 구성할 때 한 번 호출될 것이다. 그 안에서, 직관적으로 우리는 주어진 링크된 리스트를 나중에 재사용할 수 있도록 배열로 변환할 수 있다.getRandom() 함수에 관해서, 링크된 리스트를 배열로 변환하여, 우리는 간단히 이 배열에서 샘플을 채취할 수 있었다.

 

class Solution {
    private ArrayList<Integer> range = new ArrayList<>();

    /** @param head The linked list's head.
        Note that the head is guaranteed to be not null, so it contains at least one node. */
    public Solution(ListNode head) {
        while (head != null) {
            this.range.add(head.val);
            head = head.next;
        }
    }

    /** Returns a random node's value. */
    public int getRandom() {
        int pick = (int)(Math.random() * this.range.size());
        return this.range.get(pick);
    }
}
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */

The above solution is simple, which happens to be fast as well. But it comes with two caveats:

• It requires some space to keep the pool of elements for sampling, which does not meet the constraint asked in the follow-up question, i.e. a solution of constant space.

• It cannot cope with the scenario that we have a list with ever-growing elements, i.e. we don't have unlimited memory to hold all the elements. For example, we have a stream of numbers, and we would like to pick a random number at any given moment. With the above naive solution, we would have to keep all the numbers in the memory, which is not scalable.

We will address the above caveats in the next approach.

Complexity Analysis

• Time Complexity:

  • For the init(head) function, its time complexity is \mathcal{O}(N)O(N) where NN is the number of elements in the linked list.

  • For the getRandom() function, its time complexity is \mathcal{O}(1)O(1). The reason is two-fold: it takes a constant time to generate a random number and the access to any element in the array is of constant time as well.

• Space Complexity: \mathcal{O}(N)O(N)

  • The overall solution requires \mathcal{O}(N)O(N) space complexity, since we make a copy of elements from the input list.

---

Approach 2: Reservoir Sampling

Intuition

In order to do random sampling over a population of unknown size with constant space, the answer is reservoir sampling. As one will see later, it is an elegant algorithm that can address the two caveats of the previous approach.

 

일정한 공간이 있는 알 수 없는 크기의 모집단에 대해 무작위 샘플링을 하려면 저장장치 샘플링이 정답이다. 나중에 알게 되겠지만, 이전 접근법의 두 가지 주의사항을 다룰 수 있는 우아한 알고리즘이다.

The reservoir sampling algorithm is intended to sample k elements from an population of unknown size. In our case, the k happens to be one.

저장장치 샘플링 알고리즘은 알 수 없는 크기의 모집단에서 k 원소를 샘플링하기 위한 것이다. 우리의 경우, k는 우연히 하나가 된다.

 

Furthermore, the reservoir sampling is a family of algorithms which includes several variants over the time. Here we present a simple albeit slow one, also known as Algorithm R by Alan Waterman.

 

더욱이, 저장고 샘플링은 시간에 따른 여러 변형을 포함하는 알고리즘 계열이다. 여기서 우리는 Alan Waterman에 의해 Algorithm R이라고도 알려진 간단하지만 느린 것을 제시한다.

 

# S has items to sample, R will contain the result
def ReservoirSample(S[1..n], R[1..k])
  # fill the reservoir array
  for i := 1 to k
      R[i] := S[i]

  # replace elements with gradually decreasing probability
  for i := k+1 to n
    # randomInteger(a, b) generates a uniform integer
    #   from the inclusive range {a, ..., b} *)
    j := randomInteger(1, i)
    if j <= k
        R[j] := S[i]

 

 

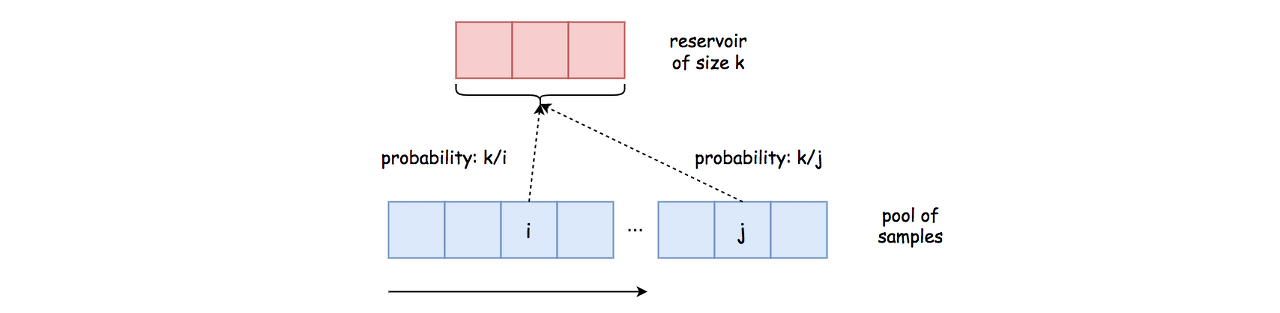
We summarize the main idea of the algorithm as follows:

• Initially, we fill up an array of reservoir R[] with the heading elements from the pool of samples S[]. At the end of the algorithm, the reservoir will contain the final elements we sample from the pool.

• We then iterate through the rest of elements in the pool. For each element, we need to decide if we want to include it in the reservoir or not. If so, we will replace an existing element in reservoir with the current element.

알고리즘의 주요 아이디어를 다음과 같이 요약한다.

• 초기에는 검체 S[]의 풀에서 표제 원소로 저장소 R[]의 배열을 채운다. 알고리즘의 끝에서 저장소는 풀에서 샘플링하는 최종 원소를 포함할 것이다.
• 그리고 나서 우리는 수영장의 나머지 요소들을 반복한다. 각 원소에 대해서는 저수지에 포함시킬지 안 할지를 결정해야 한다. 만일 그렇다면, 우리는 저장소에 있는 기존 원소를 현재 원소로 교체할 것이다.

 

One important question that one might have is that how we can ensure that each element has an equal probability to be chosen.

Given the above algorithm, it is guaranteed that at any moment, for each element scanned so far, it has an equal chance to be selected into the reservoir.

한 가지 중요한 질문은 각 원소가 선택될 확률을 동일하게 보장할 수 있다는 것이다.

위의 알고리즘을 고려할 때, 지금까지 스캔한 각 원소에 대해 어느 순간에도 저장소로 선택될 수 있는 동등한 기회가 보장된다.

 

Here we provide a simple proof.

• Suppose that we have an element at the index of i (and i > k), when we reach the element, the chance that it will be selected into the reservoir would be \frac{k}{i}ik​, as we can see from the algorithm.

• Later on, there is a chance that any chosen element in the reservoir might be replaced with the subsequent element. More specifically, when we reach the element j (j > i), there would be a chance of \frac{1}{j}j1​ for any specific element in the reservoir to be replaced. Because for any specific position in the reservoir, there is \frac{1}{j}j1​ chance that it might be chosen by the random number generator. On the other hand, there would be \frac{j-1}{j}jj−1​ probability for any specific element in the reservoir to stay in the reservoir at that particular moment of sampling.

• To sum up, in order for any element in the pool to be chosen in the final reservoir, a series of independent events need to occur, namely:

  • Firstly, the element needs to be chosen in the reservoir when we reach the element.
  • Secondly, in the following sampling, the element should remain in the reservoir, i.e. not to be replaced.

• Therefore, for a sequence of length n, the chance that any element ends up in the final reservoir could be represented in the following formula:

 

여기서 우리는 간단한 증거를 제공한다.  

• 우리가 i(그리고 i > k)의 지수에 원소를 가지고 있다고 가정하면, 우리가 원소에 도달하면, 알고리즘에서 볼 수 있듯이, 그것이 저수지로 선택될 가능성은 에프락키익일 것이다.  
• 나중에, 저수지에서 선택된 요소가 후속 요소로 대체 될 가능성이 있습니다. 보다 구체적으로, 우리가 요소 j(j > i)에 도달하면, 저장소의 특정 요소가 교체될 가능성이 있을 것이다. 왜냐하면 저수지의 어떤 특정한 위치에 대해서는, 난수 생성기에 의해 선택될 가능성이 있는 frac1jj1이 있기 때문이다. 반면에, 저수지의 특정 요소가 표본 추출의 특정 순간에 저수지에 머물 확률은 afracj-1jjj1일 것입니다.  

 

 

 

 

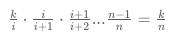
Algorithm

Given the intuition above, we can now put it into implementation as follows:

• In the init() function, we simply keep the head of the linked list, rather than converting it into array.

• In the getRandom() function, we then do a reservoir sampling starting from the head of the linked list. More specifically, we scan the element one by one and decide whether we should put it into the reservoir (which in our case case happens to be of size one).

알고리즘.위의 직관으로 볼 때, 이제 다음과 같이 실행에 옮길 수 있다. 

• init()함수에서는 단순히 연결목록의 헤드를 배열로 변환하지 않고 유지한다. 
• getRandom() 함수의 경우 링크된 목록의 머리부터 저장장치 샘플링을 수행한다. 구체적으로는 원소를 하나하나 스캔하여 저수지에 넣어야 할지를 결정한다(우리의 경우 우연히 크기가 1이 된다).

 

class Solution {
    private ListNode head;

    /** @param head The linked list's head.
        Note that the head is guaranteed to be not null, so it contains at least one node. */
    public Solution(ListNode head) {
        this.head = head;
    }

    /** Returns a random node's value. */
    public int getRandom() {
        int scope = 1, chosenValue = 0;
        ListNode curr = this.head;
        while (curr != null) {
            // decide whether to include the element in reservoir
            if (Math.random() < 1.0 / scope)
                chosenValue = curr.val;
            // move on to the next node
            scope += 1;
            curr = curr.next;
        }
        return chosenValue;
    }
}
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */

Complexity Analysis

• Time Complexity:

  • For the init(head) function, its time complexity is O(1).

  • For the getRandom() function, its time complexity is O(N) where N is the number of elements in the input list.

• Space Complexity: O(1)

  • The overall solution requires O(1) space complexity, since the variables we used in the algorithm are of constant size, regardless the input.

복잡성 분석

• 시간 복잡성:
  • init(head) 함수의 경우 시간 복잡도는 O(1)이다.
  • getRandom() 함수의 경우 시간 복잡성은 O(N)이며 여기서 N은 입력 목록의 요소 수입니다.
• 공간 복잡성: 
  • O(1)알고리즘에서 우리가 사용한 변수는 입력에 상관없이 일정한 크기이기 때문에 전체적인 솔루션에는 O(1) 공간 복잡성이 필요하다.